Лекция 7
Статистической гипотезой называется предположение о виде закона распределения случайной величины. Проверка гипотез осуществляется с помощью статистических критериев. Статистический критерий – это правило, по которому принимается решение о гипотезе. Известны критерии Стьюдента, Фишера, а также, наиболее популярный критерий Пирсона («кси в квадрате»), который имеет вид:
(расчетное значение £ табличного),
где 
– число интервалов разбиения случайной величины; 
– теоретическая вероятность и 
– относительная частота попадания случайной величины 
в 
-й интервал, 
– объем выборки.
Табличное значение критерия Пирсона имеется в прил. 5 при заданной доверительной вероятности 
. Число степепей свободы рассчитывают как 
, где 
– число параметров закона распределения, определяемых по выборке.
В случае равномерного, экспоненциального закона, а также распределения Пуассона 
, так как по выборке определяется один параметр – математическое ожидание. В случае нормального распределения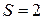 
, так как по выборке оцениваются два параметра – математическое ожидание и дисперсия.
Найденное по формуле значение 
сравнивается с табличным. Если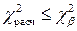 
, то гипотеза о виде распределения принимается, в противном случае она отвергается.
Пример 1. В результате семи независимых измерений некоторой физической величины получены опытные данные: Y ={12, 40, 27, 24, 28, 33, 18}. Определить к какому из законов распределения относится распределение случайной величины при доверительной вероятности 
.
Решение: Найдем числовые характеристики величины Y:
.
.
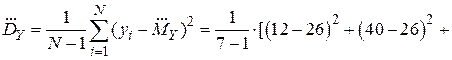
. Итак, 
, 
.
Принимаем 
. Поскольку xmin =12, xmax =40, то по формуле 
находим значение случайной величины на правой границе каждого из четырёх участков. Находим Кі, 
. Сводим все значения в табл. 1.
Таблица 1.
| № | Границы участка | Частота, K i | Относительная частота, k i | p i при равномером законе | p i при экспоненциальном законе | p i при нормальном законе |
| 12£ x <19 | 0,29 | 0,25 | 0,15 | 0,1581 | ||
| 19£ x <26 | 0,14 | 0,25 | 0,12 | 0,2764 | ||
| 26£ x <33 | 0,43 | 0,25 | 0,08 | 0,2764 | ||
| 33£ x £40 | 0,14 | 0,25 | 0,07 | 0,1581 |
а) Проверяем гипотезу о равномерном распределении.
– определяем вероятность попадания в заданный диапазон при равномерном законе распределения, используя формулу из прил. 3:
; 
;
; 
.
– определяем критерий Пирсона по формуле:
.
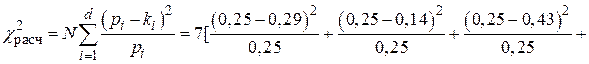
– определяем табличное значение критерия Пирсона при доверительной вероятности с помощью метода линейной интерполяции.
В прил. 5 критерий Пирсона дан не для всех значений доверительной вероятности. Если заданное значение 
в таблице отсутствует, то находим в таблице те графы, между которыми оно находится. Для равномерного закона:
Таблица 2
| Закон распределения | r | b | |
| 0,95 | 0,98 | ||
| равномерный (экспоненциальный) | 5,991 | 7,824 |
При число степеней свободы для равномерного закона равно: 
, поэтому 
; 
.
– представим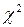 
в виде линейного уравнения вида 
, где:
.
– подставляем в формулу 
значение заданной доверительной вероятности 
, и получаем:
.
– сравниваем табличное значение критерия Пирсона 
с расчетным: 
. Неравенство выполняется, гипотеза принимается.
б) Проверяем гипотезу о экспоненциальном распределении.
Поскольку значение оценки математического ожидания 
уже вычислено ранее, то параметр 
найдём из выражения:
.
– определяем вероятность попадания в заданный диапазон при экспоненциальном законе распределения, используя формулу из прил. 3:
;
Значение функции 
находим по прил. 4:
;
;
.
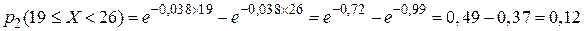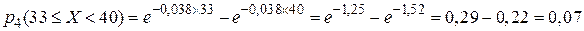
– определяем критерий Пирсона по формуле:
.
– табличное значение критерия Пирсона то же, что и у равномерного закона (для экспоненциального закона распределения тоже 
) 
.
– сравним табличное значение критерия Пирсона 
с расчетным: 
. Неравенство не выполняется, гипотеза отвергается.
в) Проверяем гипотезу о нормальном распределении.
– определяем вероятность попадания в заданный диапазон при нормальном законе распределения, используя формулу из таблицы прил. 3:
;
Значение оценки математического ожидания 
и значение оценки среднего квадратичного отклонения 
уже вычислены ранее. Значения для функции Лапласа находим из прил. 2., при этом учитываем свойство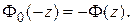 
;
;
;
.
– определяем критерий Пирсона по формуле:
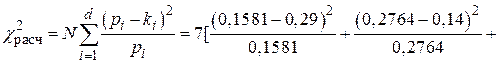
– определяем табличное значение критерия Пирсона при доверительной вероятности .
Для нормального закона распределения:
Таблица 3
| Закон распределения | r | b | |
| 0,95 | 0,98 | ||
| нормальный | 3,841 | 5,412 |
При число степеней свободы для нормального закона равно: 
, поэтому 
; 
.
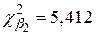– представим 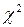в виде линейного уравнения вида , где:
.
– подставляем в формулу 
значение заданной доверительной вероятности , и получаем: 
.
– сравниваем табличное значение критерия Пирсона с расчетным: 
. Неравенство выполняется, гипотеза принимается.
Вывод: Случайная величина распределена либо по равномерному, либо по нормальному закону распределения.