Основные понятия теории графов
Простым графом называется некоторое множество вершин(точек), некоторые из которых соединены линиями(рёбрами). Вершины графа обозначаются латинскими буквами или v1, v2,…,vn. Рёбра обозначаются буквами е1, е2, …, еm или буквами вершин, которые это ребро соединяет. Число вершин графа обозначают n, а число рёбер – m. Сам граф обозначают буквой G.
| А |
| В |
| С |
| Е |
| D |
| рис.1 |
В графе на рисунке 1 число вершин n=5, рёбер m=6. Рассмотрим и остальные определения на примере этого графа.
Если две вершины соединены ребром, то они называются смежными. При этом говорят, что эти вершины инцидентны этому ребру. Например, вершины А и В смежны. А и С не смежны.
Число рёбер, инцидентных вершине(т.е. исходящих из этой вершины) называют степенью этой вершины. Обозначение: degVi.
В графе на рисунке 1
deg A= 3,
deg B = 2,
deg C = 4,
deg D = 1.
deg E = 2.
Если из вершины не выходит ни одного ребра, то она называется изолированной.
Важной характеристикой графа является последовательность степеней, записанная с учетом повторений в порядке возрастания.
Для нашего примера последовательность степеней: (1, 2, 2, 3, 4).
Каждому графу соответствует единственная последовательность степеней.
Однако не каждой последовательности чисел соответствует граф, а если и соответствует, то, возможно, не один.
Например, последовательности (1, 2, 2) не соответствует ни один граф,
а последовательности (1, 2, 2, 2, 3) соответствуют два различных графа:
Хотя иногда по данной последовательности вершин можно однозначно восстановить граф.
Например, последовательности (1, 2, 2, 3) соответствует одному графу:
Лемма о рукопожатиях.
Старинная формулировка: Число пожатых в рукопожатиях рук за всю историю человечества есть чётное число.
Формулировка в теории графов: Сумма степеней всех вершин графа есть чётное число, равное удвоенной сумме всех рёбер графа.
 .
.
Например, для графа на рисунке 1
| А |
| В |
| С |
| Е |
| D |
| рис.1 |
deg A= 3,
deg B = 2,
deg C = 4,
deg D = 1.
deg E = 2.
 .
.
Способы задания графов
1) Графический способ (рассмотрен выше).
2) Матрица смежности. Это матрица размерности nxn, все элементы которой равны:

Матрица смежности симметрична относительно главной диагонали, на которой все элементы равны нулю.
Замечание. Иногда используют разновидности матрицы смежности, где, например, вместо нулей ставят прочерки или оставляют пустые ячейки.
Например, для графа
| А |
| В |
| С |
| Е |
| D |
| рис.1 |
матрица смежности будет иметь вид:

 .
.
Из свойств матрицы смежности можно отметить, что число единиц в каждой строке(столбце) матрицы равно степени соответствующей этому ряду вершине. Число единиц выше(ниже) главной диагонали равно числу рёбер графа.
Матрица смежности однозначно(с точностью до изображения) задаёт граф.
3) Графовое число.
Вся информация, необходимая для изображения графа находится выше главной диагонали матрицы смежности. Если записать её построчно и перевести полученное число в десятичную систему исчисления, то это десятичное число и называется графовым число.
Пример.
Записать графовое число для графа на рис.1. Матрица смежности для этого графа будет иметь вид:

Запишем все подчёркнутые элементы в одну строку и переведём в десятичное число:
(1101 100 11 0)2 = (29+28+26+25+22+21)10 = (512+256+64+32+4+2)10=87010
Ответ. Графовое число 870.
По графовому числу также можно однозначно восстановить матрицу смежности, а следовательно оно однозначно задаёт и сам граф.
Пример.
Дано графовое число 1453. Восстановить по нему матрицу смежности и изобразить граф.
145310=101101011012
Разделим это число на строки, начиная с нижней, куда нужно всего одно число, выше два и т.д.
(1 0110 101 10 1)2
Для первой строки разрядов не хватило. Дополняем нулями.
(00001 0110 101 10 1)2
И восстанавливаем матрицу:

По матрице можно построить граф:
| А |
| В |
| С |
| Е |
| D |
| F |
3) Матрица Кирхгоффа(Лапласа). Это матрица размерности nxn, все элементы которой равны:

Матрица Лапласа симметрична относительно главной диагонали, на которой все элементы равны нулю. Сумма элементов каждого ряда матрицы равна нулю.
Например, для графа
| А |
| В |
| С |
| Е |
| D |
| рис.1 |
матрица Лапласа будет иметь вид:

 .
.
Матрица Лапласа обладает свойствами, аналогичными матрице смежности, т.е. она симметрична относительно главной диагонали и однозначно задаёт граф. Однако матрица Кирхгоффа(Лапласа) обладает и другими полезными свойствами. Например, в её помощью можно найти число всех каркасных деревьев графа.
4) Таблица инциденций. Этот способ задания графов используется для больших графов, когда матрица смежности будет слишком громоздкой. Например, для записи существующих рейсов авиакомпаний.
Таблица состоит из n строк. В первой ячейке строки указывается номер или название соответствующей данной строке вершины, а в следующих ячейках названия или номера вершин, смежных с данной. Таблица инциденций также однозначно задаёт граф.
Пример. Записать таблицу инциденций для графа:
| A |
| H |
| В |
| K |
| Е |
| L |
| С |
| M |
| D |
| F |

| A | B | M | |||
| B | A | C | |||
| C | B | D | K | L | M |
| D | C | E | |||
| E | D | ||||
| F | K | ||||
| H | K | ||||
| K | C | F | H | L | |
| L | C | K | M | ||
| M | A | C | L |
Меры графов
Кроме таких важных мер графов как число вершин, число рёбер, последовательностей степеней, используют и другие меры графа. Рассмотрим самые популярные из них.
Эксцентриситетом вершины графа называют число кратчайшее расстояние(т.е. наименьшее число рёбер между вершинами) до наиболее удалённой вершины графа. Обозначение 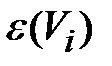 .
.
Вершина(или несколько вершин) графа с наименьшим эксцентриситетом называется центром графа.
Суммой расстояний для каждой вершины называется сумма расстояний от этой вершины до всех остальных вершин графа. Обозначение  .
.
Вершина(или несколько вершин) графа с наименьшей суммой расстояний называется центром тяжести графа.
Пример. Для изображенного графа найти центр и центр тяжести.
| В |
| рис.2 |
| А |
| С |
| Е |
| D |
| F |
Решение
Найдем эксцентриситеты вершин графа:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Следовательно, центр графа составляют вершины A, C, D.
4. Найдем сумму расстояний для каждой вершины графа:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Следовательно, центр тяжести графа находится в вершине A.
Рёберный граф
Каждому графу можно поставить в соответствие рёберный граф. Вершинами рёберного графа являются рёбра исходного графа. Они смежны, если смежны соответствующие им рёбра исходного графа.
Пример. Для графа на рисунке 1 построить рёберный граф.
| А |
| В |
| С |
| Е |
| D |
| рис.1 |
| АЕ |
| АС |
| ВС |
| СЕ |
| СD |
| АВ |
Виды графов
Граф называется связным, если в нём существует путь из любой вершины в любую другую. Граф на рисунке 1 связный.
| А |
| В |
| С |
| Е |
| D |
| рис.1 |
Полным называется граф, у которого любые две его вершины смежны, т.е. соединены ребром. Данный граф не является полным, т.к., например, вершины А и D (также как и вершины B и D, Е и D и т.д.) не смежны.
Число всех рёбер полного графа равно  .
.
На рисунке 2 представлены полные графы. Обозначаются полные графы
Кn.
| А |
| В |
| С |
| A |
| рис.2 |
| А |
| В |
| С |
| D |
| Е |
| А |
| В |
| С |
| D |
| A |
| B |
| K1 |
| K2 |
| K3 |
| K4 |
| K5 |
Графы-деревья
Деревом называется связный граф, не имеющий циклов. На рисунке 1 граф связный, но содержит циклы А-В-С и А-Е-С, поэтому не является деревом.
На рисунке 3 граф является деревом.
| А |
| В |
| С |
| Е |
| D |
| рис.3 |
Число рёбер в графе дереве на единицу меньше числа вершин.
Т.е. m=n-1.
Прибавление в граф-дерево одного ребра создает один цикл. И граф перестает быть деревом. А удаление из графа дерева хотя бы одного ребра приводит к тому, что граф перестает быть связным.
Остовным деревом связного графа называется подграф графа, содержащий все вершины исходного графа и который является деревом.
Теорема Кирхгофа. Число остовных деревьев в связном графе порядка равно алгебраическому дополнению любого элемента матрицы Кирхгофа.
Пример. Найти количество остовных деревьев графа:
| B |
| A |
| D |
| E |
| C |
Ему соответствует матрица смежности:

Найдем количество остовных деревьев графа с помощью следующей теоремы.
Построим матрицу Кирхгофа для заданного графа:
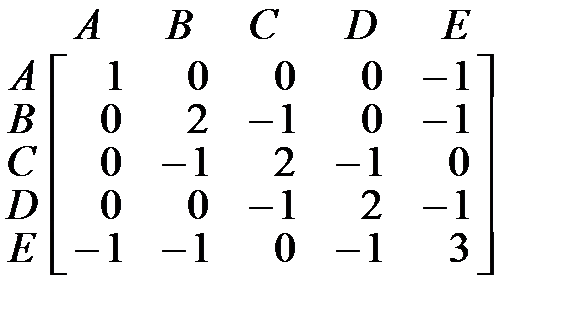
Выберем произвольный элемент матрицы Кирхгофа. Пусть это будет элемент в пятой строке и пятом столбце. Тогда число остовных деревьев в графе будет равно алгебраическому дополнению этого элемента матрицы Кирхгофа:

 .
.
Изобразим эти остовные деревья:
| A |
| BA |
| C |
| D |
| E |
| A |
| BA |
| C |
| D |
| E |
| A |
| BA |
| C |
| D |
| E |
| A |
| BA |
| C |
| D |
| E |
Ответ: 4.
Двудольным называется граф, множество вершин которого можно разделить на две доли так, чтобы вершины, находящиеся в одной доле, не были смежными.
Критерий двудольности: граф двудольный тогда и только тогда, когда он не содержит циклов нечетной длины.
На рисунке 1 граф не является двудольным, так как содержит циклы А-В-С и А-Е-С длиной 3.
Граф-дерево на рисунке 3 является двудольным. Все графы-деревья являются двудольными, так как вообще не имеют циклов.
| А |
| В |
| С |
| Е |
| D |
| рис.4 |
| F |
Данный граф не содержит циклов нечетной длины, поэтому он является двудольным, и его вершины можно разделить на две доли с помощью точного алгоритма для связного двудольного графа, основанного на методе исключения:
1 шаг. Выбираем произвольную вершину графа. Заносим её в первую долю графа. Объявляем первую долю графа текущей.
2 шаг. Просматриваем все непросмотренные вершины текущей доли. Все смежные с ними вершины заносим во вторую долю. Объявляем другую долю текущей.
3 шаг. Если не все вершины занесены в доли, то вернуться к шагу 2.
| A |
| В |
| F |
| С |
| E |
| D |
Граф называется эйлеровым, если он содержит эйлеров цикл. Цикл называется эйлеровым, если он содержит все ребра графа по одному разу (цикл начинается и заканчивается в одной вершине, вершины могут повторяться, ребра – нет).
Теорема Эйлера: граф является эйлеровым тогда и только тогда, когда он связный и степени всех его вершин четные. Граф на рисунке 1 эйлеровым не является, т. к. не выполняется теорема Эйлера (например степень вершины D равна 1).
| А |
| В |
| С |
| Е |
| D |
| рис.5 |
| F |
| H |
На рисунке 5 граф является эйлеровым, так как степени всех вершин чётные. Эйлеровых циклов здесь несколько. Один из них А-В-Н-F-B-C-F-D-C-A.
Граф называется гамильтоновым, если он содержит гамильтонов цикл. Цикл называется гамильтоновым, если он проходит через все вершины графа (вершины не могут повторяться, кроме совпадающей начальной и конечной вершины цикла, в гамильтоновом цикле не обязательно проходятся все ребра). Теоремы, однозначно определяющей, является ли данный граф гамильтоновым, нет. Граф на рисунке 1 не является гамильтоновым, т.к. невозможно построить гамильтонов цикл, проходящий через вершину D. Граф на рисунке 5 не является гамильтоновым, а на рисунке 6 граф гамильтонов.
| А |
| В |
| С |
| Е |
| D |
| рис.6 |
| F |
| H |
Планарным называется граф, который можно изобразить без пересечения рёбер.
Например, граф на рисунке 7 является планарным, так как его можно изобразить так, как на рисунке 8
| А |
| В |
| С |
| Е |
| D |
| рис.7 |
| А |
| В |
| С |
| Е |
| D |
| рис.8 |
Однозначной теоремы, отвечающей на вопрос, является ли граф планарным, нет. Но на практике доказать то, что граф не планарный часто помогает следующая теорема:
Теорема. Граф, содержащий подграф К5 или стягиваемый удалением рёбер и вершин к нему подграф, не является планарным.
В теории графов изучается ещё много различных видов графов. Кроме простых графов, рассмотренных ранее, изучаются также взвешенные графы. В которых каждому ребру поставлено в соответствие некоторое число, называемое весом графа. Весом рёбер может служить расстояние между вершинами, стоимость проезда между ними, время, пропускная способность, производительность и другие значения, которые диктуются практическими задачами.
| А |
| В |
| С |
| Е |
| D |
| рис.9 |
Взвешенные графы возможно задавать и с помощью матрицы смежности, но в случае наличия ребра вместо единиц записывается вес соответствующего ребра.
Матрица смежности графа на рисунке 9 имеет вид:

Граф, всем рёбрам которого задано направление, называется направленным графом. Рёбра при этом называются дугами. Если у вершины имеются только исходящие дуги, то она называется истоком. Если у вершины есть только входящие дуги, то она называется стоком. Направленные графы также возможно задавать с помощью матрицы смежности, но она утрачивает симметричность.
Пример.
Матрица смежности графа на рисунке 10 имеет вид:
| А |
| В |
| С |
| Е |
| D |
| рис.10 |

Вершина D является стоком, а вершина Е – истоком.
Часто используют взвешенно-направленные графы.
Например, граф на рисунке 11 является взвешенно-направленным.
| А |
| В |
| С |
| Е |
| D |
| рис.11 |
 .
.
Изоморфизм графов.
Любой абстрактный граф идентичен, или, как говорят математики, изоморфен некоторому геометрическому графу. При изображении геометрических графов имеется большая свобода в размещении вершин и в выборе формы соединяющих их ребер. Поэтому может оказаться, что один и тот же граф представляется различными чертежами, разглядывая которые далеко не сразу можно осознать, что они являются изображениями одного и того же графа. Такие геометрические графы тоже называют изоморфными.
Из определения следует, что изоморфные графы могут различаться лишь обозначениями вершин и ребер, так как у них должно быть равное число вершин и ребер, соответствующие друг другу вершины обязаны иметь одинаковые степени, и, разумеется, совершенно все равно, какую геометрическую реализацию графа выбирать для его изображения.
Для того, чтобы доказать, что два графа изоморфны необходимо переименовать их вершины таким образом, чтобы смежные вершины в одном графе были смежны и во втором. Т.е. переименовать вершины так, чтобы можно было изобразить графы одинаково или получить идентичные матрицы смежности.
Для того, чтобы доказать, что графы не изоморфны, достаточно найти у тиз хотя бы одно отличие. Например, число вершин, число ребер, отличия в последовательности степеней, цента или центра тяжести, длине минимального цикла и числе циклов, отличия в типе графа(проверка на двудольность и т.д.)
Пример. Исследовать графы на изоморфизм.
| G1 |
| G2 |
Решение. Данные графы имеют одинаковое число вершин, ребер. Однако у графа G2 есть вершина со степенью 1, а в графе G1 такой нет. Следовательно, данные графы не изоморфны.
Замечание. Для того, чтобы доказать, что графы не изоморфны, достаточно хотя бы одного отличия. Вместо исследования степеней графа можно было заметить, что второй граф двудольный, а первый нет, или то, что первый гамильтонов, а второй нет, или, например обратить внимание на длину минимального цикла(или их количество.
Нахождение наибольшей клики в графе
Кликой графа называется любой полный подграф графа.
В графе может быть несколько клик. Особый интерес представляет наибольшая по размеру клика.
Существуют точные решения проблемы наибольшей клики (например, методом ветвей и границ), однако время расчета растет экспоненциально с увеличением размерности графа.
На практике чаще используется простой жадный алгоритм:
Шаг 1. Выбрать из всех вершин графа вершину с наибольшей степенью (если имеется несколько вершин с той же степенью, то выбирается любая из них). Внести ее в множество вершин строящейся клики.
Шаг 2. Из оставшихся вершин графа найти вершину с наибольшей степенью, которая смежна со всеми вершинами строящейся клики. Если имеется несколько таких вершин, то выбирается любая из них. Внести ее в множество вершин строящейся клики. Если нет вершин, смежных со всеми вершинами строящейся клики, то перейти к шагу 4.
Шаг 3. Вернутся к шагу 2.
Шаг 4. Конец алгоритма.
Пример.
Найти наибольшую клику в графе
| С |
| H |
| A |
| F |
| D |
| B |
| E |
| K |
Применим простой жадный алгоритм, в скобках будем указывать степень вершин.
1. Выбираем из всех вершин графа вершину с наибольшей степенью. Это вершина С(6). Вносим ее в множество вершин строящейся клики {C}.
2. Из оставшихся вершин графа, находим вершины, которые смежны со всеми вершинами строящейся клики, т.е. с вершиной С.
Это вершины A(3), B(3), E(3), D(4), F(4), H(5).
Выбираем из них вершину с наибольшей степенью. Это вершина H. Вносим ее в множество вершин строящейся клики {C, H}.
3. Повторяем выполнение шага 2. Из оставшихся вершин графа, находим вершины, которые смежны со всеми вершинами строящейся клики, т.е. с вершинами С и H.
Это вершины E(3), D(4), F(4).
Наибольшую степень имеют вершины D и F. Выбираем из них любую. Пусть это будет вершина D. Вносим ее в множество вершин строящейся клики {C, H, D}.
4. Повторяем выполнение шага 2. Из оставшихся вершин графа, находим вершины, которые смежны со всеми вершинами строящейся клики.
Это вершина F(4).
Вносим ее в множество вершин строящейся клики {C, H, D, F}.
5. Повторяем выполнение шага 2.Так как нет вершин, смежных со всеми вершинами строящейся клики, то переходим к шагу 4, то есть завершаем работу алгоритма.
В результате выполнения алгоритма была найдена клика {C, H, D, F}. Она действительно является наибольшей для данного графа.
Замечание. Недостатком жадного алгоритма нахождения наибольшей клики в графе является то, что он не всегда находит именно наибольшую клику. Поэтому часто его рекомендуют «запускать» несколько раз, начиная с различных вершин с большой степенью.
Пример.
Выяснить, найдет ли жадный алгоритм наибольшую клику {A, B, D, E}.
| С |
| H |
| A |
| F |
| D |
| B |
| E |
| K |
| L |
В данном случае по алгоритму мы должны первой выбрать вершину С(6), затем смежную с ней вершину с наибольшей степенью E(5), затем вершину D(4). В результате алгоритм найдет клику {C, E, D}, которую уже нельзя увеличить, но которая не является наибольшей для этого графа.