Средние величины и их виды
К обобщающим показателям кроме относительных величин относятся и средние.
Средней величиной называется обобщающий показатель какого-либо варьирующего признака совокупности однотипных явлений.
Основная особенность использования средних величин заключается в том, что их можно вычислять только для качественно однородных совокупностей.
В статистике могут применяться различные виды средних величин:
• средняя арифметическая;
• средняя гармоническая;
• средняя квадратическая;
• средняя хронологическая;
• средняя геометрическая;
• средняя структурная;
• средняя скользящая.
Выбор формулы средней величины зависит от экономической сущности усредняемого признака, т. е. наличия тех или иных исходных данных. Наиболее распространены в статистике средняя арифметическая и средняя геометрическая величины.
Средняя арифметическая величина применяется тогда, когда объем варьирующего признака, представляет собой сумму его индивидуальных значений. Средняя арифметическая может быть простой и взвешенной.
Простая средняя арифметическая величина применяется тогда, когда каждое индивидуальное значение признака встречается один раз или одинаковое количество раз. Рассчитывается она делением суммы индивидуальных значений признака на их количество по формуле
где 
— соответственно индивидуальное значение признака;
п — количество индивидуальных значений.
Взвешенная средняя арифметическая величина применяется тогда, когда варианты в изучаемой совокупности повторяются неодинаковое количество раз и вариационный ряд несимметричен. Для вычисления средней арифметической взвешенной необходимо каждую варианту умножить на соответствующую ей частоту и сумму произведений разделить на сумму частот, т. е. формула имеет вид
где X — варианты; f — частоты.
Средняя гармоническая
Средняя гармоническая простая вычисляется по формуле:
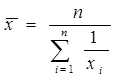
Средняя гармоническая взвешенная вычисляется по следующей формуле:
,
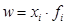- объем явлений
Средняя гармоническая взвешенная применяется тогда, когда отсутствуют действительные носители признака.
Данная формула применяется при построении средне гармонического индекса, когда нет возможности использовать агрегатную форму построения индексов, для определения изменения цены по минимальной продовольственной «корзины».
Средняя геометрическая
Средняя геометрическая простая вычисляется по формуле:
По этой формуле вычисляется биржевой индекс «Файнэшл Таймс», сложные проценты на рынке ценных бумаг, среднегодовой коэффициент роста.
Средняя геометрическая взвешенная вычисляется по формуле:
где 
- среднее значение исследуемого признака;
х -отдельные значения усредненного признака (варианты);
f- частота повторений (вес) вариант;
Средняя квадратическая используется при определении средних диаметров колес, труб, средних сторон квадратов
простая 
взвешенная 
где - среднее значение исследуемого признака;
хi -отдельные значения усредненного признака (варианты);
п -число единиц исследуемой совокупности;
fi- частота повторений (вес) вариант;
Средняя хронологическая
Средняя хронологическая вычисляется по формуле:
,
где n- число дат
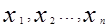– уровни ряда
Скользящая средняя
Суть расчета средней скользящей состоит в том, что по эмпирическим данным вычисляют скользящие средние, которые получают из сумм показателей, последовательно сдвигающихся на одну дату по ряду. Затем подвижные суммы следует разделить на число дат, принятых за период сглаживания. Таким образом, получаем скользящую среднюю.
Структурные средние (мода и медиана)
К структурным средним относятся мода и медиана. Мода (М0) – наиболее часто встречающееся значения признака в совокупности. Например: 2, 4, 3, 3, 3, 3, 1, 5. Мода – 3. Обычно встречаются ряды с одним модальным значением признака. В противном случае ряд называется бимодальным или мультимодальным.
В интервальном вариационном ряду модальным интервалом считается интервал с наибольшей частотой. Обычно в этом случае используется следующая формула:
где: 
- нижняя граница модального интервала;
- частота в модальном интервале;
- частота в интервале, предшествующем модальному;
- частота в интервале, следующим за модальным;
i – величина интервала.
Медиана (Ме) – середина ранжированного статистического ряда. Медиана делит ряд на две равные части. Вначале определяют порядковый номер медианы:
Nme=(n+1)/2,
где n – объем ряда (число единиц в ряду).
Если ряд состоит из четного числа членов, то медиана определяется как полусумма двух срединых вариант. Так, дан ряд 10, 20, 30, 40, 50,..., 80
Nme=(8+1)/2=4,5, Ме=(40+50)/2=45.
В интервальном вариационном ряду для нахождения медианы применяется формула:
где: Ме – медиана
- нижняя граница интервала, в котором находится медиана;
- накопленная частота в интервале, предшествующем медианному;
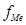- частота в медианном интервале;
i – величина интервала;
k – число групп.
В дискретном вариационном ряду медианой считается значение признака в той группе, в которой накопленная частота превышает половину числа единиц совокупности.
Аналогично медиане вычисляются значения признака, делящие совокупность на 4 равные части (по числу единиц). Эти величины называют квартилями и обозначают буквой 
Q со значком номера квартиля. 
совпадает с медианой. Первый и третий квартили рассчитываются по следующим формулам:
Значения признака, делящие ряд на 5 равных частей, называются квинтилями, на десять – децилями.