Подставляем во второй закон термодинамики и имеем

Т*dS≥ dU+P∙dV+dA* или Т∙ds≥ du+p∙dv+da*

Эти соотношения называются объединенными уравнениями первого и второго закона термодинамики или объединенным законом термодинамики.

Эксергия – техническая работоспособность единицы рабочего тела, характеризующая полезную механическую работу при переходе из состояния (P,V,T,S) в равновесное с окружающей средой(P₀,V₀, T₀,S₀).

То есть при отсутствии потерь тепла Δq=0 или Т=Т₀

A₀^max=e=(i - i₀) – T₀∙(s₀ – s)

Эксергия используется для оценки термодинамической эффективности и совершенства теплосиловых или холодильных установок.

10. Энтропия и термодинамическая вероятность

Существуют два понятия вероятности: математическая и термо­динамическая. Математической вероятностью называ­ется отношение числа благоприятных случаев к числу возможных. Например, если из каждых 100 обнаруженных месторождений 10 являются рудными, то математическая вероятность обнаружения рудного месторождения (Wм) равна Wм= 10/100== 1/10.Если в двух из десяти рудных месторождений два являются рудой на железо, то математическая вероятность обнаружения же­лезорудного месторождения будет

Wм= (10/100) • (2/10)=1/50.

Математическая вероятность всегда меньше единицы, макси­мальное ее значение Wм=1.

Прежде чем перейти к рассмотрению термодинамической веро­ятности, ознакомимся с понятиями макроскопического и микроско­пического состояний термодинамической системы.

Макроскопическое состояние системы определя­ется термодинамическими параметрами состояния. Для определе­ния макроскопического состояния системы достаточно знать два любых термодинамических параметра состояния.

Микроскопическое состояние системы определяет­ся совокупностью параметров состояния всех молекул системы. К параметрам, характеризующим микроскопическое состояние, относятся скорость, координаты положения, частота колебаний молекул и др.

Одному макросостоянию системы соответствует большое число микросостояний, т. е. любое заданное макросостояние системы мо­жет быть достигнуто большим количеством вариантов микросо­стояний.

Термодинамической вероятностью W называется число микросостояний, с помощью которых можно реализовать заданное макросостояние системы. Термодинамическая вероят­ность является целым числом, причем очень большим.

Если термодинамическая система самопроизвольно переходит из одного макросостояния в другое, то это означает, что второе макросостояние имеет большую термодинамическую вероятность, т. е. оно может быть реализовано большим количеством микросо­стояний, чем первое. Следовательно, в результате любого самопро­извольного процесса термодинамическая вероятность системы воз­растает, одновременно возрастает и ее энтропия. Взаимосвязь между энтропией и термодинамической вероятностью установил Больцман. Эта зависимость имеет вид

S=K∙lnW, (1.54)

где К— постоянная, равная постоянной Больцмана (газовая посто­янная, отнесенная к одной молекуле, K=1,38∙10^-23Дж/°С).

При увеличении температуры энтропия системы возрастает, следовательно, возрастает и термодинамическая вероятность. При абсолютном нуле температур W=1, т. е. при этой температуре макроскопическое состояние системы может быть осуществлено только единственной комбинацией составляющих систему элемен­тарных частей. В этом случае энтропия всякого тела равна нулю. Это состояние системы является самым неустойчивым.

 

11. Равновесные термодинамические системы.

Состояние равновесия – это такое состояние, к которому при данных внешних условиях стремится термодинамическая система. Различают устойчивое (стабильное), неустойчивое (лабильное) и относительно устойчивое (метастабильное) состояния.

Ранее мы установили, что для изолированной системы критерием равновесия является dS≥0:

S=S_max; dS=0; d²S<0

Если же система, каким либо образом взаимодействует с окружающей средой, то условия равновесия будут иными.

Наибольший интерес представляют четыре типа условий взаимодействия:

1) объем системы остается постоянным, но система может обмениваться теплом с окружающей средой, причем так, чтобы энтропия оставалась постоянной;

V=const, S= const.

2) система может обмениваться с окружающей средой и теплом и механической работой, но так чтобы давление и энтропия оставались постоянными;

P=const,, S= const.

3) объем системы сохраняется постоянным, но система может обмениваться с окружающей средой теплом, причем так, чтобы температура оставалась постоянной;

V=const, T=const.

4) система может обмениваться с окружающей средой и теплом и механической работой, но так чтобы давление и температура оставались постоянными

Р=const, T=const.

1.V=const, S= const следовательно dV=0 и dS=0 или dU≤ T∙dS откуда dU≤0 – критерий равновесия.

То есть с приближением к состоянию равновесия внутренняя энергия убывает, достигая min в этом состоянии

U=U_min; dU=0; d²U>0

2. P=const, S= const тогда dP=0 и dS=0

так как I= U+P∙V, то dI=dU+P∙dV+V∙dP; dU=dI-VdP имеем dI≤T∙dS+V∙dP-критерий равновесия.

То есть с приближением к равновесию энтальпия системы убывает, достигая min в равновесии

I= I_min; dI=0; d²I>0

3.V=const, T=const следовательно dV=0, dT=0 так как T∙dS= d(T∙S)-S∙dT ≥dU+P∙dV; тогда dU-d(T∙S)≤S∙dT-P∙dV или d(U-T∙S)≤-S∙dT-P∙dV откуда d(U-T∙S) ≤0.

(U – T*S) =F – свободная энергия или изохорно-изотермический потенциал; dF ≤0- критерий равновесия.

То есть с приближением к состоянию равновесия свободная энергия убывает, достигая min в состоянии равновесия.

F=F_min; dF=0; d²F>0

4.Р=const, T=const; dP=0; dT=0. dI≤T*dS+V*dP; T*dS=d(T*S)-S*dT тогда

dI-d(T*S) ≤0; dФ≤0 – критерий равновесия.

Ф=I-T*S – изобарно-изотермический потенциал или свободная энтальпия.

То есть с приближением к состоянию равновесия изобарно-изотермический потенциал системы убывает, достигая min в состоянии равновесия.

Ф=Ф_min; dФ=0; d²Ф

Величины Ф и F образованы из уравнений состояния I,U,S и следовательно сами являются функциями состояния.

Заканчивая вопрос о термодинамических потенциалах, рассмотрим понятие химического потенциала φ, называемого удельным изобарно-изотермическим потенциалом

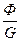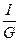φ=i-T∙s; φ= ; i= ; s=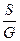

Эта величина обладает замечательным свойством: она позволяет рассчитать изменение характеристических функций любых систем при изменении количества вещества в системе (G).

Внутренняя энергия U, энтальпия I, свободная энергия F и изобарно-изотермический потенциал (свободная энтальпия) Ф, характеризующие условия равновесия термодинамических систем при различных условиях взаимодействия со средой, носят название характеристических функций.

Помимо того, что характеристические функции являются критериями равновесия в термодинамических системах, они обладают еще одним важным свойством: если мы знаем характеристическую функцию, выраженную через соответствующие, свои для каждой функции переменные, то можно вычислить любую термодинамическую величину.

12. Фазовые переходы.

Фазовым переходом называется переход вещества из од­ной фазы в другую. Частным случаем фазового перехода являет­ся переход 'вещества из одного агрегат-ного состояния (твердого, жидкого или газообразного) в другое. Так как многие вещества могут существовать в любом из агрегатных состояний в несколь­ких фазах, то понятие агрегатного состояния несколько уже поня­тия фазы. Например, кварц в твердом агрегатном состоянии при изменении температуры может перестраиваться из одной фазы в другую. Для него характерно семь фазовых состояний (α-кварц, β-кварц, β-тридимит, γ-тридимит, α-тридимит, α-кристобалит, β-кристобалит).

Минералы и горные породы в различных фазовых состояниях имеют различные физические свойства и, в частности, плотность. Это объясняется различием структур и, следовательно, различием молекулярного взаимодействия в кристаллической решетке ми­нералов при различных фазовых состояниях.

При агрегатных превращениях минералов и пород происходит выделение или поглощение некоторого количества тепла, называе­мого теплотой перехода.

При анализе фазовых переходов важную роль играет правило фаз Гиббса.

Оно устанавливает зависимость между числом независимых интенсивных переменных, определяющих состояние термодинамической системы, находящейся в равновесии (их называют степенями свободы системы), числом фаз и числом компонентов системы.

Правило фаз Гиббса свидетельствует о том, что число степе­ней свободы Ψ термодинамической системы равно числу компо­нент в ней п минус число фаз X и плюс два, т. е

Ψ=n-X+2 (2.1)

Если система однокомпонентная (чистое вещество), то правило фаз Гиббса имеет вид

Ψ =3 -X. (2.2)

Из (2.2) следует, что для чистых ве­ществ при однофазной системе (X=1) число степеней свободы равно двум, т. е. состояние термодинамической системы в этом случае может быть определено, если заданы два любых параметра. Если же система, состоящая из чистого вещества, coдepжит две фазы (Х=2), нахо­дящиеся в равновесии, то число степеней свободы равно единице. Это свидетель­ствует о том, что в этом случае состоя­ние системы может быть определено, если задан один независимый параметр. Например, если известна температура фазового перехода, то все другие термодинамические параметры определяются температурой перехода.

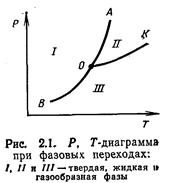
Для однокомпонентной трехфазной системы (X=3) число не­зависимых переменных равно нулю. Это свидетельствует о том, что такая система может существовать только при одном условии, параметры которого характеризуются тройной точкой (точка О на рис. 2.1) на Р, Т-диаграмме.

Согласно Р, Т-диаграмме (рис. 2.1), вещество находится в твердом состоянии при таких параметрах, которые соответствуют точкам, расположенным влево от линии АОВ. Газообразное со­стояние вещества соответствует параметрам, характеризующимся точками, расположенными вправо от линии КОВ. Жидкое состоя­ние соответствует области, расположенной между линиями ОА и ОК. Точка О называется тройной точкой, где вещество может на­ходиться одновременно в трех агрегатных состояниях. Например, для воды тройная точка характеризуется следующими параметрами:Т=0 °С и Р=610,8 Па (0,006228 кгс/см²).

Линия ОВ на Р, Т-диаграмме называется кривой сублимации, ОК — кривой кипения и ОА — кривой плавления. Кривые кипения и сублимации всегда имеют положительный наклон. Это означает, что с ростом давления температура фазового перехода возрастает. Кривая плавления может иметь как положительный, так и отри­цательный наклон, т. е. с ростом давления температура плавления может, как возрастать, так и понижаться.

Движущей силой фазовых переходов в горных породах явля­ется подводимая энергия в виде тепла. При нагревании минералов породы тепловое движение частиц в узлах кристаллической ре­шетки становится более интенсивным, связи между ними наруша­ются и решетка перестраивается в новую более устойчивую форму. При этом внутренняя энергия минералов уменьшается, а часть подведенной тепловой и накопленной минералами энергии высво­бождается, совершая внешнюю работу.

13. Уравнение Клайперона- Клаузиуса.

Рассмотрим две фазы (1 и 2), находящиеся в равновесии при давлении Р и температуре Т. Химические потенциалы (φ=i-T 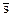) двух фаз, находящихся в равновесии при фазовом переходе, равны. Это можно записать как

φ₁(P,T)=φ₂(P,T) (2.5)

При изменении температуры фаз системы на dT она перейдет в новое равновесное состояние в том случае, если давление изме­нится на dP. Для нового равновесного состояния системы условие равновесия можно записать в виде

φ₁(P+dP,T+dT)=φ₂(P+dP,T+dT) (2.6)

Функции, стоящие в левой и правой частях уравнения (2.6), можно разложить в ряд Маклорена. В результате получим

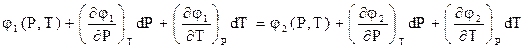(2.7)

Левая и правая части выражения (2.7) содержат функцию хими­ческих потенциалов фаз для начального равновесного состояния и полный дифференциал химического потенциала. Это выражение с учетом (2.5) можно представить в виде

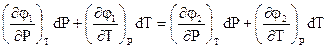(2.8)

Для изобарно-изотермических процессов имеем

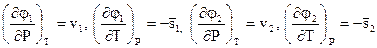(2.9)

С учетом (2.9) выражение (2.8) примет вид

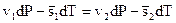(2.10)

Преобразовав (2.10), получим

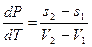(2.11)

Выражение (2.11) называется уравнением Клапейрона-Клаузиуса которое в данном виде не позволяет установить влияние теплоты фазового перехода на характер изменения давле­ния перехода при изменении температуры. Для этого представим выражение для энтальпии в дифференциальном виде

di=du+d(P∙v), (2.12)

или

du+P∙dv=di—v∙dP. (2.13)

Подставляя в (2.13) вместо d 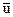+Pdv его значение из объединенного закона термодинамики, получим выражение

Td 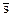=di—v∙dP, (2.14)

которое применительно к изобарным процессам примет вид

Td 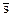=di. (2.15)

Так как при фазовых переходах температура системы не изменя­ется, то интегрирование (2.15) дает

T 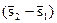= i₂ – i₁ (2.16)

Выражение (2.16) свидетельствует, что при фазовых переходах подведенное тепло T 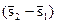расходуется на изменение энтальпии системы. Разность энтальпий (i₂ – i₁) называется удельной теплотой фазового перехода r, Дж/кг, и характеризуется количеством тепла, поглощенного или выделенного единицей массы вещества при фазовом переходе. С учетом этого выражение (2.16) можно представить в виде

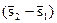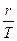= (2.17)

а уравнение Клапейрона-Клаузиуса примет вид

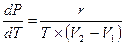(2.18)

Рассмотрим конкретные фазовые переходы «жидкость — пар», «твердое тело — жидкость» и «твердое тело — пар».

Фазовые переходы «жидкость—пар». Для данных переходов в выражении (2.18) величина r будет удельной теплотой парообразования, Дж/кг; v₂—удельным объемом пара на линии кипения V_п, м³/кг; v₁— удельным объемом жидкости на линии кипения V_ж, м³/кг; Р—равновесным давлением в точках фазово­го перехода, Па. С учетом этого уравнение Клапейрона-Клаузиуса для фазовых переходов «жидкость—пар» примет вид

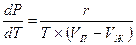(2.19)

Удельный объем пара всегда много больше удельного объема жидкости, т. е. V_п>V_ж, поэтому согласно (2.19) следует, что с ростом температуры давление при фазовых переходах «жидкость— пар» всегда увеличивается, т. е. dP/dT>0. Так как V_п>V_ж, то величину (Vп—Vж) в (2.19) можно заменить величиной V_п, которая при малых давлениях с достаточной точностью может быть опре­делена из уравнения Клапейрона, т. е.

V_п= 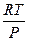(2.20)

где R—универсальная газовая постоянная, отнесенная к массе одного киломоля вещества, μ, кг/кмоль; R=8,31 • 10³ /μ, Дж/(кг.°С).

С учетом этого выражение (2.19) примет вид

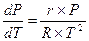(2.21)

Разделив переменные в (2.21) получим

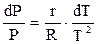(2.22)

Интегрируя левую и правую части выражения (2.22) и прини­мая во внимание, что при низких давлениях теплота фазового пере­хода «жидкость — пар» не зависит от температуры, получим

lnP=r/(R∙T)+const. (2.23)

Постоянную интегрирования в (2.23) можно определить, если известно давление при какой-либо одной фиксированной темпера­туре фазового перехода.

Фазовые переходы «твердое тело—жидкость». Для фазовых переходов «твердое тело—жидкость» уравнение Клапейрона-Клаузиуса (2.18) примет вид

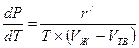(2.24)

где r'—удельная теплота плавления, Дж/кг; V_ж—удельный объ­ем жидкости на линии плавления, м³/кг; V_тв—удельный объем твердого вещества на линии плавления, м³/кг.

Если V_ж>V_тв, то с ростом давления температура фазового перехода «твердое тело—жидкость» возрастает и наоборот.

Фазовые переходы «твердое тело — пар». Для этих фазовых переходов уравнение Клапейрона-Клаузиуса (2.18) при­мет вид

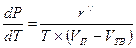(2.25)

где r" — удельная теплота сублимации, Дж/кг; V_п - удельный объем пара на линии сублимации, м³/кг; V_тв — удельный объем твердого вещества на линии сублимации, м³/кг. Так как V_п>>V_тв, то, применяя преобразования аналогичные тем, которые были при выводе уравнения (2.22), получим

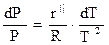(2.26)

Величина r" зависит от температуры, поэтому интегрирование правой части уравнения (2.26) возможно в том случае, когда известна функция r"=r"(Т).

Г И Д Р А В Л И К А

Гидравлика (техническая механика жидкости) – это прикладная наука, изучающая законы равновесия и движения жидкости, а также способы применения этих законов к решению инженерных задач. Первыми фактическими знаниями по гидравлике и опытом их практического применения обладали ещё в древности народы Египта, Китая, Ассирии, Греции и др. Одним из первых трудов(250 г. до н.э.), относящихся к гидравлике, является трактат Архимеда «О плавающих телах», известный теперь как закон Архимеда.

ХV1 и ХV11вв крупные научные работы принадлежат Леонардо да Винчи - движение по трубам и открытым руслам. Галилео Галилею – в области равновесия и движения тел в жидкости. Эванджелиста Торричелли – по истечению жидкости через отверстия. Блезу Паскалю – о передаче давления жидкости (закон Паскаля). Исааку Ньютону – о внутреннем трении в жидкости (закон Ньютона).

Гидромеханика (гидравлика) как наука сформировалась в ХVIII в Российской академии наук благодаря работам Даниила Бернулли, Леонарда Эйлера и М В Ломоносова.

ОБЩИЕ СВЕДЕНИЯ О ЖИДКОСТИ

1.Основные понятия и определения.

Одно и тоже вещество, имеющее молекулярное строение, может находиться в разных агрегатных состояниях (твердом, жидком, газообразном, плазменном), обусловленных различиями в тепловом движении молекул и в их взаимодействии. Переход из одного состояния в другое сопровождается скачкообразным изменением ряда физических свойств. (Вода – в зависимости от давления и температуры м.б. жидкой, газообразной или твердой.

Жидкость – это материальная среда (вещество), обладающее свойством текучести, т.е. способностью неограниченно деформироваться под действием приложенных сил. Данное свойство обусловлено диффузией молекул.

В зависимости от механических свойств жидкости подразделяются на две группы: капельные – практически несжимаемые (вода, ртуть, масла и др.) это термин «капельная жидкость» или жидкость; газообразные – легко сжимаемые (воздух, газы)- «газообразная жидкость» или газ.

Одной из моделей жидкости широко используется в гидравлике - гипотеза сплошной среды, в соответствии которой, абстрагируясь от молекулярного строения, жидкость рассматривается как сплошная непрерывная среда (континуум), полностью занимающая все пространство, в котором оно находится, без разрывов и пустот. Размеры занимаемого жидкостью пространства несоизмеримо больше размеров межмолекулярных расстояний и самих молекул.

Данная гипотеза (модель) позволяет рассматривать все механические характеристики жидкости (плотность, скорость, давление и т. д.) как функции координат точки в пространстве и времени, следовательно, любая функция, которая характеризует состояние жидкости, непрерывна и дифференцируема.

2.Основные физические свойства жидкости.

Плотность – важнейшая характеристика жидкости, представляющая собой массу однородного вещества единичного объема:

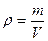
Размер плотности [ρ]= L^-3M, единица СИ килограмм на кубический метр (кг/м³).

Относительная плотность – безразмерная величина, представляющая собой отношение плотности рассматриваемого вещества к плотности стандартного вещества в определенных физических условиях:

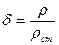
В качестве стандартного вещества принимают: для твердых и капельных жидкостей –дистиллированную воду плотностью 1000 кг/м³ при температуре 277 К (4⁰С) и давлении 101,3 кПа (760 мм рт. Ст.); для газов - атмосферный воздух плотностью 1,2 кг/м³ при т-ре 293 К (20⁰С), давлении 101,3 кПа и относительной влажности 50% (стандартные условия). Для измерения плотности в технике часто используют приборы – ареометры.

Сжимаемость- способность жидкости изменять свой объем при изменении давления и (или) температуры.

Плотность капельных жидкостей – p=ρ₀ (1- β_t ∙Δt +β_p ∙Δp),

Где ρ₀-плотность жидкости при начальных температуре и давлении; Δt и Δp – приращения температуры и давления; β_t и β_p – коэффициенты температурного расширения и объёмного сжатия, представляющие собой относительные изменения объёма жидкости при изменении соответственно температуры или давления на одну единицу:

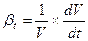β_t; ;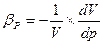

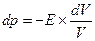
величина обратная β_p, называется модулем упругости жидкости Е_ж =1/ β_p.

Числовые значения коэффициентов β_t и β_p весьма малы.

При решении большинства практических задач изменением плотности капельных жидкостей при изменении температуры или давления обычно пренебрегают (за исключением задач о гидравлическом ударе, об устойчивости и колебании гидравлических систем и некоторых других, в которых приходится учитывать сжимаемость жидкости, а также за исключением ряда тепловых расчетов, в которых необходим учет изменения температуры жидкости).

Плотность газов в значительной степени зависит от температуры и давления. Используя известное уравнение Клапейрона – Менделеева (уравнение состояния идеального газа)

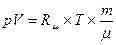
или pυ =RT, или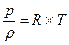

где р – абсолютное давление; V – объём; m – масса; R_μ – универсальная газовая постоянная, равная 8,314 Дж/(мольК); Т –абсолютная температура; μ - молекулярная масса; υ =V/ m –удельный объём; R=R_μ/ μ– газовая постоянная [ для воздуха R = 287 Дж/(кг*К), для метана R = 518 Дж/(кг*К)], можно установить зависимость плотности газа от температуры и давления:

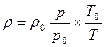
где ρ и ρ₀ плотности газа соответственно при новых давлении р и т-ре Т и начальных давлении р₀ и температуре Т₀.

Оценить сжимаемость жидкостей можно и другим путем. Так, в состоянии покоя характерным параметром сжимаемости жидкости является скорость распро-странения в ней звуковых колебаний – скорость звука

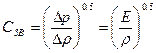- формула Лапласа

где ∆р – приращение давления; ∆ρ – приращение плотности жидкости.

Чем больше скорость звука, тем меньше сжимаемость данной жидкости и наоборот.

Если жидкость движется, то для оценки ее сжимаемости пользуются обычно не абсолютным значением скорости звука, а отношением скорости потока v к скорости звука с_зв в данной жидкости, которое называется числом Маха М= v/ с_зв.

Если скорость движения жидкости мала по сравнению со скоростью распространения в ней звука, то есть число Маха значительно меньше 1, то, независимо от абсолютного значения скорости звука, капельная жидкость или газ при таком движении можно считать практически несжимаемыми.

Растворимость. Все жидкости в определенной мере поглощают и растворяют газы. Объем газа, который может раствориться в капельной жидкости до ее полного насыщения, равен

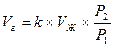
где V_г –объем газа при начальном давлении p₁; V_ж – объем жидкости при конечном давлении p₂; k – коэффициент растворимости (например при температуре +20⁰С коэффициент растворимости воздуха в воде равен 0,016).

Понижение давления, в какой либо точке гидросистемы влечет за собой выделение в этом месте газа в виде мелких пузырьков и образование пены. Последняя может появляться также при засасывании воздуха в гидросистему через неплотности или при сбросе жидкости в резервуар с некоторой высоты. Наличие пузырьков и особенно пены наряду с уменьшением плотности и увеличением сжимаемости жидкости нарушает сплошность потока и нормальную работу гидросистем.

Таблица

Давление насыщенных паров жидкостей, кПа.

Жидкость	Температура жидкости, 0С
Вода	2,34	7,38	19,9	47,4
Масло: АМГ-10 И-20А
-	-	0,4	0,8	1,73	3,06	5,72
-	-	0,13	0,27	0,4	0,53	0,93

Парообразование, кипение, кавитация. При изменении давления и температуры капельной жидкости до определенных значений, при которых давление становиться равным давлению насыщенного пара р_н.п этой жидкости при данной температуре, происходит изменение количественных характеристик капельной жидкости, и последняя скачкообразно переходит в новое качество: в жидкости образуются пузырьки и даже целые полости, заполнение паром и растворенными в ней газами. Данный процесс называется парообразованием. Достигая свободной поверхности капельной жидкости, пузырьки лопаются, и пар улетучивается – происходит кипение жидкости.

Если жидкость находится в замкнутом пространстве, то пузырьки остаются в ней, нарушая сплошность капелькой жидкости. Когда давление жидкости превысит давление насыщенного пара, снова происходит скачкообразный переход в новое качество, пар почти мгновенно конденсируется, а газы растворяются в капельной жидкости. Тогда в образовавшиеся пустоты с большой скоростью устремляются частицы капельной жидкости, окружавшей пузырьки, что приводит к почти мгновенному (за тысячные доли секунды) их смыканию. Это, в свою очередь, вызывает значительный рост давления (до нескольких МПа) в местах смыкания пузырьков, сопровождающийся характерным шумом, а также местное повышение температуры. Рассмотренный выше процесс называется кавитацией.

Кавитация в трубопроводах и гидравлических машинах – крайне вредное явление, т.к. она вызывает их эрозию, возникающую в результате многократного местного повышения давления, сопровождающегося ударами частиц капельной жидкости о стенки труб и проточных частей гидромашин. Эрозия обычно усиливается также химическим и электрохимическим воздействиями выделяющегося из воды воздуха, богатого кислородом. При длительной работе трубопроводов и гидромашин в режиме кавитации происходит разрушение указанных выше элементов.

Капиллярность - это способность капельной жидкости, находящейся в трубке малого диаметра (капилляре), подниматься выше свободной поверхности в резервуаре, образуя вогнутый мениск (если жидкость смачивает стенки трубки), или опускаться ниже свободной поверхности, образуя выпуклый мениск (если жидкость не смачивает стенки трубки). Данная поверхность жидкости обусловлена ее поверхностным натяжением и молекулярными силами взаимодействия между жидкостью и стенками трубки.

Как известно из курса физики, высота поднятия или опускания жидкости в трубке

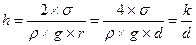
где σ- поверхностное натяжение; ρ- плотность жидкости; d=2∙r – диаметр трубки; k= 4∙ σ/(ρ∙g)- величина, постоянная для каждой конкретной жидкости. Подставляя в формулу определенные значения диаметра трубки d в мм, можно получить значения этой постоянной; для воды k= +30мм², для спирта k= +11 мм²; для ртути k= -10 мм².

Вязкость – свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой (сдвигу).

При движении вязкой жидкости между ее соседними слоями, а также между жидкостью и стенками русла возникают силы внутреннего трения и вызванные ими касательные напряжения, что приводит к различию скоростей частиц в слоях потока и деформации (сдвигу) слоев.

Если предположить, что поток состоит из отдельных слоев бесконечно малой толщины, то скорости этих слоев будут изменяться по некоторому закону от нулевого значения (у стенки) до максимального значения (в центре потока).

Согласно гипотезе, высказанной впервые в 1686 г И. Ньютоном (теоретически,обоснованной в 1883г проф. Н.П. Петровым) сила внутреннего трения T, возникающая между двумя слоями движущейся прямолинейно жидкости, прямо пропорциональна площади поверхности F соприкасающихся слоев, градиенту скорости du/dy, а также зависит от рода жидкости и температуры:

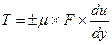
где μ – динамическая вязкость, зависящая от рода жидкости и температуры.

Жидкости, в которых силы внутреннего трения не описываются уравнением, называются аномальными, или неньютоновскими. К ним относятся цементные и глинистые растворы, смолы, некоторые масла при температурах, близких к температурам их застывания, коллоиды и др. Вода, воздух, спирт, ртуть, большинство масел, применяемых в гидроприводах, относятся к обычным – ньютоновским жидкостям.

Разделив обе части последнего уравнения на F, получим касательное напряжение (напряжение трения)

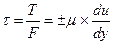- это закон трения Ньютона.

Так как Т и τ всегда положительны, то уравнения употребляются со знаком «+» если du/dy положительно, и со знаком «-», если du/dy отрицательно.

В соответствии с этими уравнениями

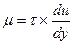
Следовательно, динамическая вязкость μ численно равна касательному напряжению τ при градиенте скорости du/dy= 1, то есть имеет вполне определенный физический смысл и полностью характеризует вязкость жидкости.

Размерность динамической вязкости [μ]= L^-1MT^-1, единица СИ – паскаль-секунда (Па∙с).

При выполнении технических расчетов в гидравлике обычно пользуются кинематической вязкостью ν, представляющей собой отношение динамической вязкости жидкости к ее плотности: ν =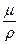

Размерность кинематической вязкости [ν ]=L²T^-1, единица СИ – м² /с.

Для определения вязкости жидкостей применяются приборы, называемые вискозиметрами.

Вязкость зависит от рода жидкости, ее температуры и давления.

При повышении температуры вязкость капельных жидкостей уменьшается, а газообразных – увеличивается. Для различных жидкостей зависимость вязкости от температуры различна, поэтому выразить ее аналитически общим уравнением невозможно.

Для расчета параметров минеральных масел, применяемых в гидроприводах, в интервале значений температуры от 30 до 150⁰С и вязкости до 10⁰ВУ (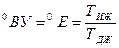 Т_иж – время истечения испытываемой жидкости, Т_дв - время истечения дистиллированной воды) можно пользоваться зависимостью: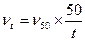

где ν _t и ν₅₀ – кинематическая вязкость масла соответственно при данной температуре (t,⁰C) и температуре 50⁰С; n –показатель степени, зависящий от условной вязкости масла при значении температуры 50⁰С:

0ВУ50	1,2	1,5	1,8	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0
n	1,39	1,59	1,72	1,79	1,99	2,13	2,24	2,32	2,42	2,49	2,52	2,56

 

Для большинства капельных жидкостей с повышением давления вязкость несколько увеличивается.

В интервале значений давления от 0 до 50 МПа вязкость минеральных масел, применяемых в гидроприводах, изменяется практически линейно и может быть вычислена по эмпирической формуле

ν_р = ν₀∙ (1+k_p∙∙p),

где ν_р и ν₀ – кинематическая вязкость масла соответственно при давлении p(МПа) и атмосферном давлении; k_p – опытный коэффициент, зависящий от марки масла. Для легких масел (ν<15∙10^-6м²/с) k_p=0,02, для тяжелых (ν>15∙10^-6м²/с) k_p=0,03).

Для других жидкостей зависимости вязкости от давления и температуры приведены в справочной литературе.

3.Силы, действующие в жидкости.

Жидкость в состоянии покоя или движения находится под действием различных сил, которые в соответствии с их природой можно разделить на две группы – поверхностные и массовые.

Поверхностные силы приложены к поверхности, ограничивающей рассматриваемый объем жидкости. При равномерном распределении этих сил по данной поверхности их числовое значение пропорционально числовому значению площади. К поверхностным силам относятся силы, действующие на поверхность жидкости по перпендикулярным направлениям (силы давления), по касательной силы поверхностного натяжения, а также силы внутреннего трения (последние имеют место только при движении жидкости).

Массовые силы действуют на все частицы рассматриваемого объема жидкости. При равномерном распределении этих сил по данному объему их числовое значение пропорционально числовому значению массы (объема). К массовым силам относятся силы тяжести и силы инерции.

В настоящем курсе жидкость рассматривается как сплошная непрерывная среда, в которой отсутствуют силы, действующие в точке. Поэтому в отличие от динамики твердых тел в гидравлике обычно рассматривают не сами силы, а плотность их распределения в сплошной среде: либо предел отношения элементарной поверхностной силы к элементарной площади, либо предел отношения элементарной массовой силы к элементарной массе рассматриваемого объема жидкости, то есть единичные силы.

Единичные поверхностные силы представляют собой напряжения – касательные τ или нормальные σ (при сжатии жидкости напряжение сжатия называется давлением р), а единичные массовые силы – ускорения j.

ГИДРОСТАТИКА

Гидростатика – это раздел гидравлики, в котором изучаются законы равновесия жидкостей, а также твердых тел, погруженных в жидкость.

1.Давление в точке покоящейся жидкости и его свойства.

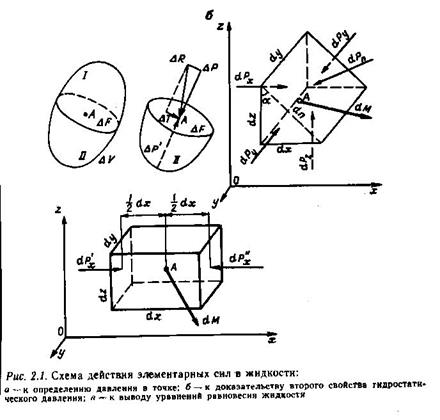Мысленно выделим вокруг точки «А», находящейся внутри покоящейся жидкости, элементарный объем ΔV, рассечем его на две части произвольной плоскостью, проходящей через точку «А» (рис)(а) и отбросим одну из частей этого объема. Для того чтобы оставшаяся часть по-прежнему находилась в равновесии, заменим действие отброшенной части на площадку ΔF с распределенными по ней элементарными по-верхностными силами. Предположим, что равнодействующая этих элементарных сил ΔR действует в нап-равлении, показанном на рис «а». Разложим ΔR на две составляющие, расположенные в плоскости сечения – ΔТ, нормально к этой плоскости – ΔР.

Очевидно, чт