Механика
1. Поступательное движение. Основные кинематические характеристики движения: траектория, длина пройденного пути, перемещение, скорость, ускорение. Тангенциальная и нормальная составляющие ускорения.
Поступательное движение — это механическое движение системы точек (абсолютно твёрдого тела), при котором отрезок прямой, связывающий две любые точки этого тела, форма и размеры которого во время движения не меняются, остаётся параллельным своему положению в любой предыдущий момент времени. Поступательное движение не является противоположностью движению вращательному, а в общем случае может рассматриваться как совокупность поворотов — не закончившихся вращений. При этом подразумевается, что прямолинейное движение есть поворот вокруг бесконечно удалённого от тела центра поворота.
В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе.
Математически поступательное движение по своему конечному результату эквивалентно параллельному переносу. Однако, рассматриваемое как физический процесс, оно представляет собой в трёхмерном пространстве вариант винтового движения.
Линию, по которой движется материальная точка в пространстве, называют траекторией.
Длиной пути точки называется сумма длин всех участков траектории, пройденных этой точкой за рассматриваемый промежуток времени s = s (t). Длина пути — скалярная функция времени.
Перемещением материальной точки за некоторый промежуток времени называется вектор перемещения ∆r=r-r0, направленный от положения точки в начальный момент времени к ее положению в конечный момент.
Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета.
Ускорение характеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета.
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения. Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой аn. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении. 
2. Кинематика вращательного движения. Угол поворота, угловая скорость, угловое ускорение. Связь между линейными и угловыми величинами.
Пусть некоторая точка движется по окружности радиуса r D. Изменение положения точки в пространстве за промежуток времени t определяется углом поворота  (рис. 3). Элементарный поворот на угол
(рис. 3). Элементарный поворот на угол  можно рассматривать как вектор
можно рассматривать как вектор  . Модуль вектора
. Модуль вектора  равен углу поворота, а его направление совпадает с направлением поступательного движения острия правого винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.
равен углу поворота, а его направление совпадает с направлением поступательного движения острия правого винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.

Угловой скоростью  называется векторная величина, равная пределу отношения угла поворота
называется векторная величина, равная пределу отношения угла поворота  Dк промежутку времени t D, за который этот поворот произошел, при стремлении t к нулю:
Dк промежутку времени t D, за который этот поворот произошел, при стремлении t к нулю:
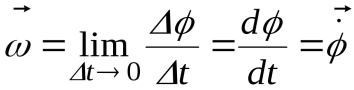 ,
,
где  – первая производная от функции угла поворота
– первая производная от функции угла поворота  радиус-вектора
радиус-вектора  по времени t. Эту производную принято обозначать, как
по времени t. Эту производную принято обозначать, как 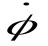 .
.
Вектор  направлен вдоль оси вращения в соответствии с правилом правого винта (рис. 3).
направлен вдоль оси вращения в соответствии с правилом правого винта (рис. 3).
Угловым ускорением 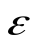 называется векторная величина, равная пределу отношения изменения угловой скорости
называется векторная величина, равная пределу отношения изменения угловой скорости  Dк промежутку времени t D, за который это изменение произошло, при стремлении t к нулю:
Dк промежутку времени t D, за который это изменение произошло, при стремлении t к нулю:
 ,
,
где  – первая производная от функции
– первая производная от функции  по времени t,
по времени t,
 –вторая производная от функции
–вторая производная от функции  по времени t.
по времени t.
Эти производные принято обозначать соответственно в виде:  и
и  .
.
Вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном вращении направление вектора 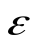 совпадает с направлением вектора угловой скорости
совпадает с направлением вектора угловой скорости  , а при замедленном – противоположно ему.
, а при замедленном – противоположно ему.
Кинематические параметры поступательного и вращательного движения связаны между собой. Связь скорости  и угловой скорости
и угловой скорости  определяется следующим образом:
определяется следующим образом:  .
.
В векторном виде эту связь для векторов  и
и  можно записать с помощью векторного произведения:
можно записать с помощью векторного произведения:  .
.
Ускорение а также можно выразить через угловые параметры, разложив ускорение а на две составляющие  и
и  , то есть:
, то есть:  .
.
Тангенциальная составляющая  выражается через угловое ускорение
выражается через угловое ускорение  :
:
 ,
,
а нормальная составляющая  – через угловую скорость
– через угловую скорость  :
:
 .
.
Тогда ускорение:  .
.
3. Законы Ньютона. Второй закон Ньютона как основное уравнение динамики. Закон сохранения импульса.
Зако́ны Нью́то́на — три важнейших закона классической механики, которые позволяют записать уравнения движения для любой механической системы, если известны силы, действующие на составляющие её тела. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год). В ньютоновском изложении механики, широко используемом и в настоящее время, эти законы являются аксиомами, базирующимися на обобщении экспериментальных результатов.
Второй закон Ньютона - основной закон динамики поступательного движения - отвечает на вопрос, как изменяется движение тела под действием приложенных к нему сил.
II закон. Ускорение материальной точки совпадает по направлению с действующей на нее силой и равно отношению этой силы к массе материальной точки.
 , где
, где  - равнодействующая сила.
- равнодействующая сила.
Силу можно выразить формулой
 ,
, 
1Н - это сила, под действием которой тело массой 1 кг получает ускорение 1м/с2 в направлении действия силы.
Второй закон Ньютона можно записать в другом виде, введя понятие импульса (Ломоносов это сделал впервые).
Импульс - векторная величина, численно равная произведению массы тела на его скорость и сонаправленная с вектором скорости.



 =
=  - основное уравнение динамики поступательного движения:
- основное уравнение динамики поступательного движения:
скорость изменения импульса материальной точки равна действующей на нее силе.
Согласно этому закону, изменение импульса материальной точки равно импульсу действующей на нее силы:

4. Механическая работа и мощность. Кинетическая и потенциальная энергия. Закон сохранения механической энергии.
Если действующая на тело сила вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой механической работой (или, сокращенно, просто работой).
Механическая работа А - скалярная величина, равная произведению модуля силы F, действующей на тело, и модуля перемещения s, совершаемого телом в направлении действия этой силы.

Если направления перемещения тела и приложенный силы не совпадают, то работу можно вычислить как произведение модулей силы и перемещения, умноженному на косинус угла α между векторами силы  и перемещения
и перемещения  (рис. 1.18.1):
(рис. 1.18.1):

Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).
Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы. 
Работа силы  : : 
|
Если проекция  силы
силы  на направление перемещения
на направление перемещения  не остается постоянной, работу следует вычислять для малых перемещений Δ si и суммировать результаты:
не остается постоянной, работу следует вычислять для малых перемещений Δ si и суммировать результаты:
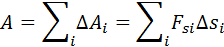
Это сумма в пределе (Δ si → 0) переходит в интеграл.
Графически работа определяется по площади криволинейной фигуры под графиком Fs (x) (рис. 1.18.2).
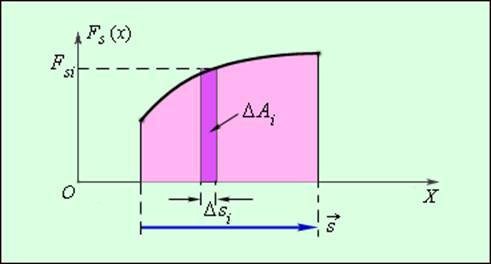
|
| Рисунок 1.18.2. Графическое определение работы. Δ Ai = Fsi Δ si |
Примером силы, модуль которой зависит от координаты, может служить сила упругости пружины, подчиняющаяся закону Гука. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу  модуль которой пропорционален удлинению пружины (рис. 1.18.3).
модуль которой пропорционален удлинению пружины (рис. 1.18.3).
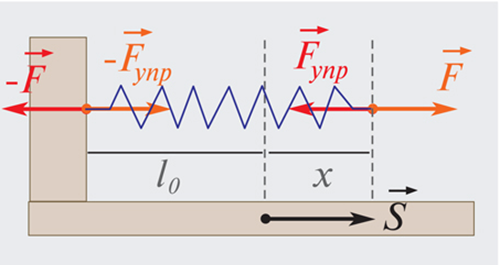
|
Рисунок 1.18.3.
Растянутая пружина. Направление внешней силы  совпадает с направлением перемещения совпадает с направлением перемещения  : :
 k – жесткость пружины.
k – жесткость пружины. 
|
Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис. 1.18.4).

|
| Рисунок 1.18.4. Зависимость модуля внешней силы от координаты при растяжении пружины |
По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
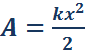
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы  равна по модулю работе внешней силы
равна по модулю работе внешней силы  и противоположна ей по знаку.
и противоположна ей по знаку.
Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.
Мощность
Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.

5. Момент инерции. Теорема Штейнера. Расчёт момента инерции однородного сплошного цилиндра относительно его геометрической оси.
Моментом инерции J материальной точки относительно оси называется скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси:
J = mr2
Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек:


К определению момента инерции точки.
Если масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объемы dv, каждый из которых обладает массой dm.
В результате получается следующее выражение:
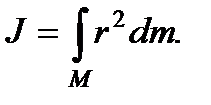
Для однородного по объему тела плотность ρ постоянна, и записав элементарную массу в виде:
dm = ρdv, преобразуем формулу следующим образом:

Размерность момента инерции – кг*м2.
Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.
Момент инерции — это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения. Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.
Всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое. Аналогично массе момент инерции является величиной аддитивной.
В некоторых случаях теоретический расчёт момента инерции достаточно прост. Ниже приведены моменты инерции некоторых сплошных тел правильной геометрической формы относительно оси, проходящей через центр тяжести.
момент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:
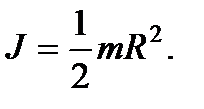
Момент инерции шара радиуса R:

Момент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:

Момент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:

Момент инерции относительно других осей вращения определяется при помощи теоремы Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции Jc относительно параллельной оси, проходящей через центр инерции тела, и величины произведения массы тела на квадрат расстояния между ними. где m масса тела, а - расстояние от центра инерции тела до выбранной оси вращения, т.е.
 , где m - масса тела, а - расстояние от центра
, где m - масса тела, а - расстояние от центра
инерции тела до выбранной оси вращения.
Покажем на одном примере применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же интегралу (*),но взятому в других пределах: 
Расстояние до оси, проходящей через центр масс, равно а = ℓ/2. По теореме Штейнера получаем тот же результат.
 .
.
Момент инерции бесконечно тонкого диска и сплошного цилиндра. Предполагается, что диск и цилиндр однородны, т. е. вещество распределено в них с постоянной плотностью. Пусть ось Z проходит через центр диска С перпендикулярно к его плоскости (рис. 4.6). Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r и наружным радиусом r + dr. Площадь такого кольца dS = 2 p rdr. Его момент инерции найдется по формуле (4.17), он равен dIz = r 2 dm. Момент инерции всего диска определяется интегралом  Ввиду однородности диска dm =
Ввиду однородности диска dm =  , где S = p R 2 – площадь всего диска. Вводя это выражение под знак интеграла, получим
, где S = p R 2 – площадь всего диска. Вводя это выражение под знак интеграла, получим
 (4.18)
(4.18)
Формула (4.18) дает также момент инерции однородного сплошного цилиндра относительно его продольной геометрической оси.
6. Кинетическая энергия вращающегося твёрдого тела.
Пусть тело вращается вокруг оси z. Мысленно разбиваем тело на элементарные массы  ,
,  …
…  , находящиеся от оси вращения на расстояниях
, находящиеся от оси вращения на расстояниях  ,
,  …
…  (рис.3.6)
(рис.3.6)

Рис.3.6
При вращении твердого тела элементарные объемы массами  опишут окружности различных радиусов
опишут окружности различных радиусов  . Причем
. Причем 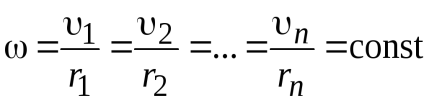 .
.
Линейную скорость i -частицы выразим через угловую скорость:  .
.
Кинетическая энергия i -ой элементарной частицы:
 . (3.6)
. (3.6)
Кинетическая энергия вращающегося твердого тела:
 , (3.7)
, (3.7)
где I – момент инерции.
Из сравнения формул  и
и  следует, что момент инерции – мера инертности тела при вращательном движении.
следует, что момент инерции – мера инертности тела при вращательном движении.
7. Понятие момента силы и момента импульса. Закон сохранения момента импульса.
Пусть некоторое тело под действием силы F, приложенной в точке А, приходит во вращение вокруг оси ОО' (рис. 1.14).
 Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль момента силы относительно точки О:
Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль момента силы относительно точки О:
М = Fp=Frsinα.
Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:
 (3.1)
(3.1)
Единица момента силы — ньютон-метр (Н • м).
Направление М можно найти с помощью правила правого винта.
Моментом импульса частицы называется векторное произведение радиус-вектора частицы на её импульс:
 или в скалярном виде L = гPsinα
или в скалярном виде L = гPsinα
Эта величины векторная и совпадает по направлению с векторами ω.
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этиммомент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
В упрощённом виде:  , если система находится в равновесии.
, если система находится в равновесии.
8. Вращение твёрдого тела вокруг неподвижной оси. Основной закон динамики вращательного движения абсолютно твёрдого тела относительно неподвижной оси.
Вращением твёрдого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела остаются неподвижными в течение всего времени движения. При этом также остаются неподвижными все точки тела, расположенные на прямой, проходящей через его неподвижные точки. Эта прямая называется осью вращения тела.

Пусть точки A и B неподвижны. Вдоль оси вращения направим ось  . Через ось вращения проведём неподвижную плоскость
. Через ось вращения проведём неподвижную плоскость  и подвижную
и подвижную  , скреплённую с вращающимся телом (при
, скреплённую с вращающимся телом (при 
 ).
).
Положение плоскости  и самого тела определяется двугранным углом между плоскостями
и самого тела определяется двугранным углом между плоскостями  и
и  . Обозначим его
. Обозначим его  . Угол
. Угол  называется углом поворота тела.
называется углом поворота тела.
Положение тела относительно выбранной системы отсчета однозначно определяется в любой момент времени, если задано уравнение 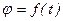 , где
, где  - любая дважды дифференцируемая функция времени. Это уравнение называется уравнением вращения твёрдого тела вокруг неподвижной оси.
- любая дважды дифференцируемая функция времени. Это уравнение называется уравнением вращения твёрдого тела вокруг неподвижной оси.
У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием только одного параметра – угла  .
.
Угол  считается положительным, если он откладывается против часовой стрелки, и отрицательным – в противоположном направлении. Траектории точек тела при его вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях перпендикулярных оси вращения.
считается положительным, если он откладывается против часовой стрелки, и отрицательным – в противоположном направлении. Траектории точек тела при его вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях перпендикулярных оси вращения.
Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела
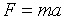 , (1.6)
, (1.6)
где F – сила, приложенная к телу массой m; а – линейное ускорение тела.
Если к твердому телу массой m в точке А (рис. 5) приложить силу F, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение  и соответственные линейные ускорения, как если бы на каждую точку действовала сила
и соответственные линейные ускорения, как если бы на каждую точку действовала сила  . Для каждой материальной точки можно записать:
. Для каждой материальной точки можно записать:
 ,
,
где  , поэтому
, поэтому
 , (1.7)
, (1.7)
где mi – масса i- й точки;  – угловое ускорение; ri – ее расстояние до оси вращения.
– угловое ускорение; ri – ее расстояние до оси вращения.
Умножая левую и правую части уравнения (1.7) на ri, получают
 , (1.8)
, (1.8)
где  – момент силы – это произведение силы
– момент силы – это произведение силы  на ее плечо
на ее плечо  .
.
Плечом силы называют кратчайшее расстояние от оси вращения “ОО” (рис. 5) до линии действия силы  .
.

Рис. 5. Твердое тело, вращающееся под
действием силы F около оси “ОО”
 – момент инерции i -й материальной точки.
– момент инерции i -й материальной точки.
Выражение (1.8) можно записать так:
 . (1.9)
. (1.9)
Просуммируем левую и правую части (1.9) по всем точкам тела:
 .
.
 Обозначим
Обозначим  через М, а
через М, а 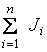 через J, тогда
через J, тогда
(1.10)
Уравнение (1.10) – основной закон динамики вращательного движения твердого тела. Величина  – геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение
– геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение  .
. 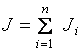 – алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».
– алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».
Мгновенное значение углового ускорения  , есть первая производная угловой скорости
, есть первая производная угловой скорости  по времени
по времени 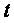 , то есть
, то есть
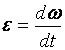 , (1.11)
, (1.11)
где  – элементарное изменение угловой скорости тела за элементарный промежуток времени
– элементарное изменение угловой скорости тела за элементарный промежуток времени 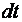 .
.
Если в выражение основного закона (1.10) поставить значение мгновенного ускорения (1.11), то
 или
или  , (1.12)
, (1.12)
где  – импульс момента силы – это произведение момента силы
– импульс момента силы – это произведение момента силы  на промежуток времени
на промежуток времени 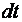 .
.
 – изменение момента импульса тела,
– изменение момента импульса тела,  – момент импульса тела есть произведение момента инерции J на угловую скорость
– момент импульса тела есть произведение момента инерции J на угловую скорость  , а
, а  есть
есть  .
.
Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы  , действующий на вращательное тело, равен изменению его момента импульса
, действующий на вращательное тело, равен изменению его момента импульса  ”:
”:
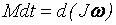 или
или 
9. Закон всемирного тяготения. Сила тяжести и вес. Поле тяготения.
Формулировка - между любыми материальными точками существует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки
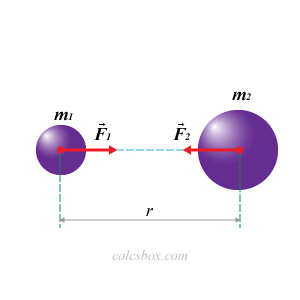
Ньютон обобщил законы движения небесных тел и выяснил, что сила F равна:
F=Gm1m2/R2
где m1 и m2 - массы взаимодействующих тел, RR— расстояние между ними, G — коэффициент пропорциональности, который называется гравитационной постояннойгравитационной постоянной. Численное значение гравитационной постоянной опытным путем определил Кавендиш, измеряя силу взаимодействия между свинцовыми шарами.
Физический смысл гравитационной постоянной вытекает из закона всемирного тяготения. Если m1=m2=1кг, R=1м, то G=F, т. е. гравитационная постоянная равна силе, с которой притягиваются два тела по 1 кг на расстоянии 1 м.
Численное значение:
G=6,67⋅10−11Н⋅м2/кг2
Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах (или если хотя бы масса одного из тел велика). Закон же всемирного тяготения выполняется только для материальных точек и шаров (в этом случае за расстояние принимается расстояние между центрами шаров).
Сила тяжести
Частным видом силы всемирного тяготения является сила притяжения тел к Земле (или к другой планете). Эту силу называют силой тяжести. Под действием этой силы все тела приобретают ускорение свбодного падения.

Сила тяжести – это сила, с которой Земля притягивает тело, находящееся на её поверхности или вблизи этой поверхности.
В соответствии со вторым законом Ньютона g=FТ/m, следовательно, FT=mg.
Если M – масса Земли, R – ее радиус, m – масса данного тела, то сила тяжести равна
F=GM/R2m=mg.
Сила тяжести всегда направлена к центру Земли. В зависимости от высоты h над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения. На поверхности Земли и в средних широтах ускорение свободного падения равно 9,831 м/с2.
Вес тела
В технике и быту широко используется понятие веса тела.
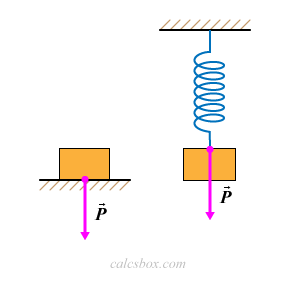
Весом тела называют силу, с которой тело давит на опору или подвес в результате гравитационного притяжения к планете.
Вес тела обозначается P. Единица веса — ньютон (Н). Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо определить, чему равна сила реакции опоры.
При этом предполагается, что тело неподвижно относительно опоры или подвеса.
Вес тела и сила тяжести отличаются по своей природе: вес тела является проявлением действия межмолекулярных сил, а сила тяжести имеет гравитационную природу.
Состояние тела, в котором его вес равен нулю, называют невесомостью. Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением, поэтому в корабле наблюдается состояние невесомости.
Закон всемирного тяготения, устанавливая зависимость силы тяготения от масс взаимодействующих тел и расстояния между ними, не даёт ответа на вопрос о том, как осуществляется это взаимодействие.
Тяготение (гравитационное взаимодействие), в отличие от таких механических взаимодействий, как удар, трение и т.д., принадлежит к особой группе взаимодействий. Оно проявляется между телами, удаленными друг от друга. Причем сила тяготения не зависит от того, в какой среде эти тела находятся. Тяготение существует и в вакууме.
Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения (гравитационного поля).
Поле – это объективная реальность, посредством которой передаётся взаимодействие. Поле, наряду с веществом, является одним из видов материи.
Итак, гравитационное поле порождается телами и, так же как вещество и другие физические поля (например, электромагнитное), является одной из форм материи.
Основное свойство поля тяготения, которое отличает его от других полей, состоит в том, что на любую материальную точку массой m, внесенную в это поле, действует сила притяжения F, пропорциональная m:  . Отсюда
. Отсюда
 , ,
| (7.2.1) |
где  – вектор, не зависящий от m и названный напряженностью поля тяготения.
– вектор, не зависящий от m и названный напряженностью поля тяготения.
Вектор напряженности  численно равен силе, действующей со стороны поля на материальную точку единичной массы, и совпадает с этой силой по направлению.
численно равен силе, действующей со стороны поля на материальную точку единичной массы, и совпадает с этой силой по направлению.
Вектор напряженности является силовой характеристикой гравитационного поля и изменяется при переходе от одной точки поля к другой.
Поле тяготения является центральным и сферически симметричным.
Поле называется центральным, если во всех его точках векторы напряжённости направлены вдоль прямых, которые пересекаются в одной и той же точке О, неподвижной относительно какой-либо инерционной системы отсчета. Точка О называется центром сил.
Центральное поле называют сферически симметричным, если численное значение вектора напряженности зависит только от расстояния r до центра сил О: G = G (r).
При наложении нескольких полей тяготения напряженность результирующего поля равна векторной сумме напряженностей всех этих полей:  .
.
Этот принцип вытекает из принципа независимости действия сил и называется принципом суперпозиции (наложения полей).
10. Упругие силы. Закон Гука. Энергия упругой деформации.
ОПРЕДЕЛЕНИЕ
Деформациями называются любые изменения формы, размеров и объема тела. Деформация определяет конечный результат движения частей тела друг относительно друга.
ОПРЕДЕЛЕНИЕ
Упругими деформациями называются деформации, полностью исчезающие после устранения внешних сил.
Если груз, подвешенный на проволоке, растягивает подвес и опускается, значит, сила тяжести совершает работу. За счет такой работы увеличивается энергия деформированного тела, которое перешло из ненапряженного состояния в напряженное. Получается, что при деформации внутренняя энергия тела увеличивается. Рост внутренней энергии тела заключается в увеличении потенциальной энергии, которая связана со взаимным расположением молекул тела. Если мы имеем дело с упругой деформацией, то после снятия нагрузки, дополнительная энергия исчезает, и за ее счет силы упругости совершают работу. В ходе упругой деформации температура твердых тел существенно не увеличивается. В этом состоит их значительное отличие от газов, которые при сжатии нагреваются. При пластической деформации твердые тела могут значительно увеличивать свою температуру. В повышении температуры, след