Закон равномерного распределения энергии по степеням свободы (закон Больцмана)

Закон о равнораспределении энергии по степеням свободы утверждает, если система частиц находится в состоянии термодинамического равновесия, то средняя кинетическая энергия хаотического движения молекул, приходящаяся на 1 степень свободы поступательного и вращательного движения, равна

Следовательно, молекула, имеющая степеней свободы, обладает энергией

, (11.2)

где – постоянная Больцмана; – абсолютная температура газа.

Внутренняя энергия идеального газа – это сумма кинетических энергий всех его молекул.

Находим внутреннюю энергию 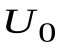одного моля идеального газа. , где – средняя кинетическая энергия одной молекулы газа, – число Авогадро (число молекул в одном моле). Постоянная Больцмана 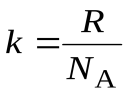. Тогда

.

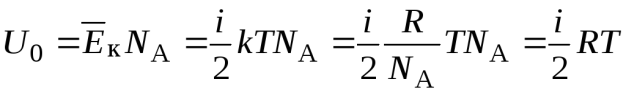Если газ имеет массу 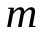, то – число молей, где – масса моля, и внутренняя энергия газа выражается формулой

. (11.3)

Внутренняя энергия идеального газа зависит только от температуры газа. Изменение внутренней энергии идеального газа определяется изменением температуры и не зависит от процесса, при котором это изменение произошло.

Изменение внутренней энергии идеального газа

, (11.4)

где – изменение температуры.

Закон равномерного распределения энергии распространяется на колебательное движение атомов в молекуле. На колебательную степень свободы приходится не только кинетическая энергия, но и потенциальная, причём среднее значение кинетической энергии, приходящейся на одну степень равно среднему значению потенциальной энергии, приходящемуся на одну степень свободы и равно

Следовательно, если молекула имеет число степеней свободы i = i _{поступат} + i _вращат + i _колеб, то средняя суммарная энергия молекулы: , а внутренняя энергия газа массы :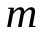

. (11.5)

7. Первое начало термодинамики. Работа газа при изменении его объёма. Расчёт работы газа в изопроцессах.

Первое начало термодинамики - один из трех основных законов термодинамики, представляющий собой закон сохранения энергии для систем, в которых существенное значение имеют тепловые процессы.

Одна из формулировок звучит следующим образом: энергия не создается и не уничтожается. Возможны лишь превращения энергии из одного вида в другой в строго эквивалентных количествах.

Согласно первому началу термодинамики, термодинамическая система (например, пар в тепловой машине) может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии.

Первое начало термодинамики объясняет невозможность существования вечного двигателя 1-го рода, который совершал бы работу, не черпая энергию из какого-либо источника.

Сущность первого начала термодинамики заключается в следующем:

При сообщении термодинамической системе некоторого количества теплоты Q в общем случае происходит изменение внутренней энергиисистемы DU и система совершает работу А:

Q = DU + A (4)

Уравнение (4), выражающее первое начало термодинамики, является определением изменения внутренней энергии системы (DU), так как Q и А — независимо измеряемые величины.

Внутреннюю энергию системы U можно, в частности, найти, измеряя работу системы в адиабатном процессе (то есть при Q = 0): А_ад = — DU, что определяет U с точностью до некоторой аддитивной постоянной U₀:

U = U + U₀ (5)

Первое начало термодинамики утверждает, что U является функцией состояния системы, то есть каждое состояние термодинамической системы характеризуется определённым значением U, независимо от того, каким путём система приведена в данное состояние (в то время как значения Q и А зависят от процесса, приведшего к изменению состояния системы). При исследовании термодинамических свойств физической систем первое начало термодинамики обычно применяется совместно со вторым началом термодинамики.

Для рассмотрения конкретных процессов найдем в общем виде внешнюю работу, совершаемую газом при изменении его объема. Рассмотрим, например, газ, на­ходящийся под поршнем в цилиндриче­ском сосуде (рис. 78). Если газ, расширя­ясь, передвигает поршень на бесконечно малое расстояние d l, то производит над ним работу

d A=Fdl=pSdl=pdV,

где S — площадь поршня, S dl=dV — из­менение объема системы. Таким образом, d A=pdV. (52.1)

Полную работу A, совершаемую газом при изменении его объема от V ₁до V ₂, найдем

 

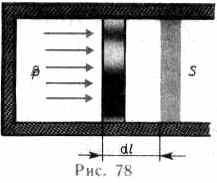
интегрированием формулы (52.1):

Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение (52.2) справедливо при любых изменениях объема твердых, жидких и га­зообразных тел.

Произведенную при том или ином про­цессе работу можно изобразить графиче­ски с помощью кривой в координатах р, V. Например, изменение давления газа при его расширении изобразится кривой на рис. 79. При увеличении объема на dV совершаемая газом работа равна pdV, т. е. определяется площадью полоски с основанием d V на рисунке. Поэтому полная работа, совершаемая газом при расширении от объема V ₁до объема V ₂, определяется площадью, ограниченной осью абсцисс, кривой p = f(V) и прямыми V₁ и V₂.

Графически можно изображать только равновесные процессы — процессы, состо­ящие из последовательности равновесных состояний. Они протекают так, что измене­ние термодинамических параметров за ко­нечный промежуток времени бесконечно мало. Все реальные процессы неравновес­ны (они протекают с конечной скоростью), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медленнее процесс протекает, тем он ближе к равновесному). В дальнейшем рассматриваемые процессы будем считать равновесными.

Изотермический процесс - процесс изменения состояния термодинамической системы при постоянной температуре

T = const, PV = const, ∆U = const, A = RT*ln ()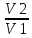

Изобарный процесс - процесс изменения состояния термодинамической системы при постоянном давлении

P = const, = const, ∆Q= ∆U + ∆A, A = P(V2-V1)

Изохорный процесс - процесс изменения состояния термодинамической системы при постоянном объёме

V = const,

 

8. Теплоёмкость. Классическая теория теплоёмкости идеальных газов и её ограниченность.

Средняя энергия одной молекулы равна: ,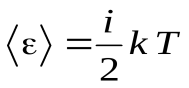

где i – число степеней свободы молекулы.

Внутренняя энергия 1 моля идеального газа, содержащего число Авогадро молекул, равна ^.

^{Для n молей газа внутренняя энергия равна .}

Теплоёмкостью тела называется количество теплоты, которое нужно подвести к телу, чтобы повысить его температуру на 1 градус (например, теплоёмкость калориметра):

^С _ТЕЛА ^{[Дж/К]. (44)}

Теплоёмкость 1 моля называют молярной теплоёмкостью С (или С _mК)]. Тогда×) [Дж/(моль

Q = C _m (n T ₂ – T ₁). (45)

Теплоёмкость единицы массы вещества называют удельной теплоёмкостью с К)]. Тогда×[Дж/(кг

Q = c m (T ₂ – T ₁). (46)

Молярная и удельная теплоёмкости связаны через молярную массу:

(47)

(или C _{m v} = M c_v, C _{m p} = M c_p, где c_V и c_P см. далее).

Пусть нагревание 1 моля газа происходит при V = const. dТогда из первого начала термодинамики следует А = 0 и dQ = dU, и молярная теплоёмкость при постоянном объёме равна

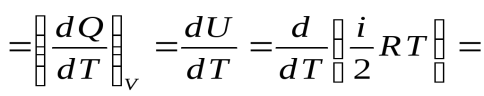
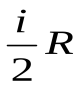. (48)

Из уравнения (48) можно получить важне соотношение:

dU = C_V dT молей равна n, а внутренняя энергия U n = C_V T.

Пусть нагревание 1 моля газа происходит при p = const. Тогда молярная теплоёмкость при постоянном давлении равна

.

Разделим уравнение первого начала термодинамики на dT:

^{, , .}

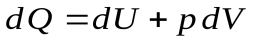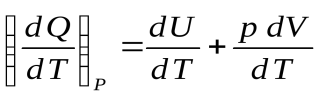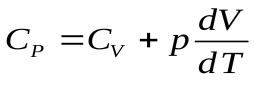Для нахождения производной dV / dT выразим объём из уравнения Менделеева-Клапейрона для 1 моля: V = RT / p. Итак:

^.

 

Мы получили уравнение Майера:

. (49)

dКроме того, выражение A / dT = R определяет физический смысл газовой постоянной R: газовая постоянная численно равна работе, которая совершается при расширении 1 моля идеального газа, нагретого на 1 градус при постоянном давлении.

Молярная теплоёмкость при постоянном давлении может быть выражена из уравнения Майера (49):

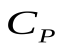
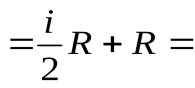
^{. (50)}

Отношение теплоёмкостей

(51)

представляет собой характеристическую для каждого газа величину (это показатель адиабаты).

Для одноатомного газа (i = 1,67.g= 3)

Для двухатомного газа (i = 1,4.g= 5)

Для трехатомного газа (i = 1,33.g= 6)

Полученные формулы для теплоёмкости дают хорошее совпадение с экспериментом для одноатомных и многих двухатомных газов (H ₂, O ₂, N ₂) при комнатной температуре. Однако существуют и различия эксперимента и теории, которые объясняются квантовой теорией теплоёмкости.

9. Адиабатный процесс. Уравнение адиабаты. Работа газа в адиабатном процессе.

Адиабатический процесс - это такое изменение состояний газа, при котором он не отдает и не поглощает извне теплоты. Следовательно, адиабатический процесс характеризуется отсутствием теплообмена газа с окружающей средой. Адиабатическими можно считать быстро протекающие процессы. Так как передачи теплоты при адиабатическом процессе не происходит, то и уравнение I начала термодинамики принимает вид

(9.20)

или

т.е. внешняя работа газа может производиться вследствие изменения его внутренней энергии. Адиабатное расширение газа (dV>0) сопровождается положительной внешней работой, но при этом внутренняя энергия уменьшается и газ охлаждается (dT<0).

Сжатие газа (dV0, т.е. адиабатное сжатие газа сопровождается его нагреванием.

Найдем связь между параметрами состояния идеального газа (например, Р и V) в адиабатическом процессе. Для этого перепишем (9.20) в форме

а величину найдем из уравнения Менделеева - Клапейрона

Таким образом, или, учитывая, что для идеального газа Разделим обе части этого уравнения на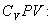

где безразмерная величина, называемая постоянной адиабаты. Пренебрегая зависимостью 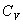от температуры, можно считать, что для данного газа . Интегрируя последнее уравнение

получим 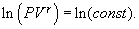т.е.

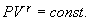
(9.21)

Это выражение называют уравнением Пуассона. Соотношение между давлением и температурой, а также между объемом и температурой идеального газа в адиабатическом процессе имеют вид

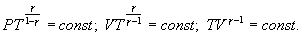
Эти соотношения легко получить из (9.21), пользуясь уравнением Менделеева - Клапейрона. Линию, изображающую адиабатический процесс в диаграмме состояния, называют адиабатой. На рис. 9.7 сплошной линией показан вид адиабаты в (P-V) диаграмме. Для сравнения в том же рисунке пунктирной линией изображена изотерма, соответствующая температуре газа в начальном состоянии 1. Так как для любого идеального газа показатель адиабаты , то в (P-V) диаграмме адиабата всегда идет круче, чем изотерма. Объясняется это тем, что при адиабатическом сжатии увеличение давления обусловлено не только уменьшением объема газа, как при изотермическом сжатии, то также еще и увеличения температуры. При адиабатическом расширении температура газа уменьшается, поэтому давление газа падает быстрее, чем при изотермическом расширении.

Работу, совершаемую газом в адиабатическом процессе, найдем интегрируя выражение

Полная работа

Из уравнения Майера (9.18) и выражения для показателя адиабаты γ следует, что

Поэтому

(9.22)

В соответствии с соотношением

Следовательно, выражение (9.22) для работы можно представить в виде

или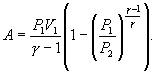

10. Круговые процессы (циклы). Обратимые и необратимые процессы. Второе начало термодинамики.

Пусть в результате некоторого процесса в изолированной системе тело переходит из состояния А в состояние В и затем возвращается в начальное состояние А. Процесс называется обратимым, если возможно осуществить обратный переход из В в А через те же промежуточные состояния, что и в прямом процессе, чтобы не осталось никаких изменений и в самом теле и в окружающих телах. Если же обратный процесс невозможен, или по окончании процесса в окружающих телах и в самом теле остались какие-либо изменения, то процесс является необратимым.

Примеры необратимых процессов. Любой процесс сопровождаемый трением является необратимым (теплота, выделяющаяся при трении не может без затраты работы другого тела собраться и вновь превратиться в работу). Все процессы, сопровождаемые теплопередачей от нагретого тела к менее нагретому, является необратимыми (например, теплопроводность). К необратимым процессам также относятся диффузия, вязкое течение. Все необратимые процессы являются неравновесными.

Равновесные – это такие процессы, которые представляют из себя последовательность равновесных состояний. Равновесное состояние – это такое состояние, в котором без внешних воздействий тело может находиться сколь угодно долго. (Строго говоря, равновесный процесс может быть только бесконечно медленным. Любые реальные процессы в природе протекают с конечной скоростью и сопровождаются рассеянием энергии. Обратимые процессы – идеализация, когда необратимыми процессами можно пренебречь).

Круговой процесс (цикл). Если тело из состояния А в состояние В переходит через одни промежуточные состояния, а возвращается в начальное состояние А через другие промежуточные состояния, то совершается круговой процесс, или цикл.

Круговой процесс является обратимым, если все его части обратимы. Если какая-либо часть цикла необратима, то и весь процесс необратим.

	Различают прямой цикл, или цикл тепловой машины и обратный цикл, или цикл холодильной машины. Совершенная за цикл работа равна разности между количеством теплоты, полученной телом при расширении и количество теплоты, отданным при сжатии. Работа в координатах равна площади цикла (рис. 15.1): .

 

11. Энтропия и термодинамическая вероятность. Аналитическое выражение второго начала термодинамики.

Второе начало термодинамики вводит в рассмотрение новую функцию состояния – энтропию. Термин «энтропия», предложенный Р. Клаузиусом, образован от греч. entropia и означает «превращение».

Уместно будет привести понятие «энтропия» в формулировке А. Зоммерфельда: «Каждая термодинамическая система обладает функцией состояния, называемой энтропией. Энтропия вычисляется следующим образом. Система переводится из произвольно выбранного начального состояния в соответствующее конечное состояние через последовательность состояний равновесия; вычисляются все проводимые при этом к системе порции тепла dQ, делятся каждая на соответствующую ей абсолютную температуру Т, и все полученные таким образом значения суммируются (первая часть второго начала термодинамики). При реальных (неидеальных) процессах энтропия изолированной системы возрастает (вторая часть второго начала термодинамики)».

Учета и сохранения количества энергии еще недостаточно для того, чтобы судить о возможности того или иного процесса. Энергию следует характеризовать не только количеством, но и качеством. При этом существенно, что энергия определенного качества самопроизвольно может превращаться только в энергию более низкого качества. Величиной, определяющей качество энергии, и является энтропия.

Процессы в живой и неживой материи в целом протекают так, что энтропия в замкнутых изолированных системах возрастает, а качество энергии понижается. В этом и есть смысл второго начала термодинамики.

Если обозначить энтропию через S,то

что и соответствует первой части второго начала по Зоммерфельду.

Можно подставить выражение для энтропии в уравнение первого начала термодинамики:

dU = T × dS – dU.

Эта формула известна в литературе как соотношение Гиббса. Это фундаментальное уравнение объединяет первое и второе начала термодинамики и определяет, по существу, всю равновесную термодинамику.

Второе начало устанавливает определенное направление течения процессов в природе, то есть «стрелу времени».

Наиболее глубоко смысл энтропии вскрывается при статической оценке энтропии. В соответствии с принципом Больцмана энтропия связана с вероятностью состояния системы известным соотношением

S = K × LnW,

где W – термодинамическая вероятность, а К – постоянная Больцмана.

Под термодинамической вероятностью, или статическим весом, понимается число различных распределений частиц по координатам и скоростям, соответствующих данному термодинамическому состоянию. При любом процессе, который протекает в изолированной системе и переводит ее из состояния 1 в состояние 2, изменение Δ W термодинамической вероятности положительно или равно нулю:

ΔW = W₂– W₁≥ 0

В случае обратимого процесса ΔW = 0, то есть термодинамическая вероятность, постоянна. Если происходит необратимый процесс, то Δ W > 0 и W возрастает. Это означает, что необратимый процесс переводит систему из менее вероятного состояния в более вероятное. Второе начало термодинамики является статистическим законом, оно описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему, то есть энтропия характеризует меру беспорядочности, хаотичности частиц в системе.

Р. Клаузиус определил второе начало термодинамики так:

► невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому (1850).

В связи с этой формулировкой в середине XIX в. была определена проблема так называемой тепловой смерти Вселенной. Рассматривая Вселенную как замкнутую систему, Р. Клаузиус, опираясь на второе начало термодинамики, утверждал, что рано или поздно энтропия Вселенной должна достигнуть своего максимума. Переход теплоты от более нагретых тел к менее нагретым приведет к тому, что температура всех тел Вселенной будет одинаковой, наступит полное тепловое равновесие и все процессы во Вселенной прекратятся – наступит тепловая смерть Вселенной.

Ошибочность вывода о тепловой смерти Вселенной заключается в том, что нельзя применять второе начало термодинамики к системе, которая является не замкнутой, а бесконечно развивающей системой. Вселенная расширяется, галактики разбегаются со скоростями, которые нарастают. Вселенная нестационарна.

В основу формулировок второго начала термодинамики положены постулаты, являющиеся результатом многовекового человеческого опыта. Кроме указанного постулата Клаузиуса наибольшую известность получил постулат Томсона (Кельвина), который говорит о невозможности построения вечного теплового двигателя второго рода (perpetuum mobile), то есть двигателя, полностью превращающего теплоту в работу. Согласно этому постулату, из всей теплоты, полученной от источника тепла с высокой температурой – теплоотдатчика, только часть может быть превращена в работу. Остальная часть должна быть отведена в теплоприемник с относительно низкой температурой, то есть для работы теплового двигателя необходимы по крайней мере два тепловых источника различной температуры.

Этим и объясняется причина, по которой нельзя перевести в работу теплоту окружающей нас атмосферы или теплоту морей и океанов при отсутствии таких же масштабных источников теплоты с более низкой температурой.

12. Цикл Карно. КПД цикла Карно.

Французский инженер Сади Карно предложил идеальный цикл, который даёт максимальное КПД т.е. . Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно.

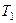- изотермическое расширение при , - адиабатическое расширение, , - изотермическое сжатие при , - изотермическое сжатие, .

Вычислим КПД цикла Карно для идеального газа. При изотермическом процессе внутренняя энергия идеального газа остаётся постоянной. Поэтому количество полученной газом теплоты равно работе , совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2). Эта работа равна

,

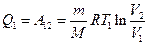где – масса идеального газа в тепловой машине.

Количество отдаваемой холодильнику теплоты равно работе , затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна

.

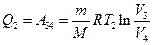Для того чтобы цикл был замкнутым, состояние 1 и 4 должны лежать на одной и той же адиабате. Отсюда вытекает условие

.

Аналогично для состояний 2 и 3 должно вытекать условие

.

Разделив одно соотношение на другое, приходим к условию замкнутости цикла

.

Теперь подставляя и в выражение для КПД, получим

. (2)

В результате получим формулу для КПД цикла Карно:

,

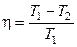где 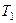- температура нагревателя, - температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах 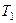и .

Вернёмся к соотношению (2), которое имеет место в случае обратимого цикла Карно. В общем случае при возможности необратимого цикла Карно это соотношение примет вид:

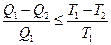. (3)

Преобразуем (3) следующим образом:

, , или

В результате получим

.

Для обратимого цикла Карно: ,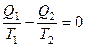

для необратимого цикла Карно: .

Для произвольного обратимого цикла:

,

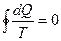для произвольного необратимого цикла:

.

13. Реальные газы. Уравнение Ван-дер-Ваальса.

Реальным называется газ, между молекулами которого действуют силы межмолекулярного взаимодействия, состоящие из сил притяжения и сил отталкивания.

Для получения уравнения состояния реального газа необходимо учесть собственный объем молекул и энергию взаимодействия молекул на расстоянии. Наличие собственного объема молекул приводит к уменьшению объема, предоставленного молекулам, на некоторую величину. Силы притяжения между молекулами газа вызывают уменьшение давления молекул газа на стенки сосуда на некоторую величину р_i.

Это уравнение может получено путем соответствующего изменения уравнения Менделеева-Клапейрона путем внесения в него поправок.

Уравнение состояния реального газа (уравнение Ван-дер-Ваальса) для одного моля имеет вид:

,

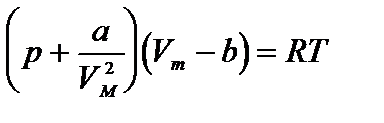где р - давление, оказываемое на стенки сосуда, V_М – объем одного моля газа, а и b - постоянные Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые опытным путем. Поправка – внутреннее давление, обусловленное силами взаимного притяжения между молекулами. Поправка b характеризует ту часть объем, которая недоступна для движения молекул. Она равна учетверенному собственному объему молекул, содержащихся в моле газа:

b = N_A.

Уравнение Ван-дер-Ваальса для произвольной массы газа имеет вид:

 

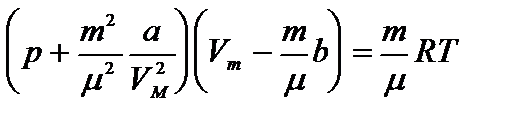
Уравнение Ван-дер-Ваальса позволяет построить теоретические изотермы реального газа и сравнить их с изотермами идеального газа и экспериментальными изотермами реального газа.

Уравнение Ван-дер-Ваальса после нескольких преобразований можно записать в виде:

.

Это уравнение третьей степени относительно V. Кубическое уравнение может иметь либо три вещественных корня, либо один вещественный и два мнимых.

14. Фазовые равновесия и превращения. Фазовые переходы первого и второго рода. Диаграмма состояния вещества.

Фазой называется термодинамическое равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Переход вещества из одной фазы в другую – фазовый переход - всегда связан с качественными изменениями свойств тела. Примером фазовых переходов могут служить изменения агрегатного состояния. Но понятие «фазовый переход» шире, т.к. оно включает и переход вещества из одной модификации в другую при сохранении агрегатного состояния (полиморфизм), например, превращение алмаза в графит.

Различают два вида фазовых переходов:

Фазовый переход 1 рода – сопровождается поглощением или выделением теплоты, изменением объема и протекает при постоянной температуре. Примеры: плавление, кристаллизация, испарение, сублимация (возгонка) и др.

Фазовые переходы 2 рода – протекают без выделения или поглощения тепла, с сохранением величины объема, но скачкообразным изменением теплоемкости. Примеры: переход ферромагнитных минералов при определенных значениях давления и температуры в парамагнитное состояние (железо, никель); переход некоторых металлов и сплавов при температуре близкой к 0⁰К в сверхпроводящее состояние (ρ = 0 Ом∙м) и др.

Для химически однородного вещества понятие фазы совпадает с понятием агрегатное состояние. Рассмотрим для такой системы фазовые превращения, используя для наглядности диаграмму состояния. На ней в координатах р и Т задается зависимость между температурами фазовых переходов и давлением. Эти зависимости в виде кривых испарения (ОИ), плавления (ОП) и сублимации (ОС) и образуют диаграмму состояния.

Точка О пересечения кривых определяет условия (значения Т и р), при которых все три агрегатные состояния вещества находятся в термодинамическом равновесии.

По этой причине она называется тройной точкой. Например, тройная точка воды является одной из реперных точек температурной шкалы Цельсия (0⁰С). Как следует из уравнения Клапейрона – Клаузиуса характер зависимости Т =f(р) для перехода твердое тело – жидкость (кривые ОП) может быть разным: Если вещество при переходе в жидкую фазу увеличивает объем (вода, висмут, германий, чугун …), то ход этой зависимости представлен на рис. 2а. Для веществ, уменьшающих объём при переходе в жидкую фазу, зависимость имеет вид показанный на рис. 2б.

Кривая испарения заканчивается критической точкой – К. Как видно из диаграммы, существует возможность непрерывного перехода жидкости в газообразную фазу без пересечения кривой испарения, т.е. без присущих такому переходу фазовых превращений.

При давлении меньшим, чем р_тр.тчк., вещество может существовать только в двух фазах: твердой и газообразной. Причем, при температурах, меньших Т_тр.тчк., возможен переход из твердого состояния в газ минуя жидкую фазу. Такой процесс называется сублимацией или возгонкой. Удельная теплота сублимации

τ_суб = λ_пл +r_исп