Основы молекулярной физики и термодинамики

1. Идеальный газ. Уравнение состояния идеального газа. Смеси газов.

Идеальным газом называется газ, молекулы которого имеют пренебрежимо малый размер и не взаимодействуют на расстоянии. А при столкновениях взаимодействуют, как абсолютно упругие шары. Идеальный газ – абстракция. Но это понятие полезное, так как упрощает инженерные расчеты тепловых машин и процессов в них происходящих. Основными параметрами газа, характеризующими его состояние являются объем, , давление, , и температура, .

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

· — давление,

· — молярный объём,

· — универсальная газовая постоянная

· — абсолютная температура,К.

Так как , где —количество вещества, а , где — масса, —молярная масса, уравнение состояния можно записать:

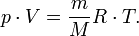
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

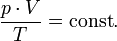
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

— закон Бойля — Мариотта.

— Закон Гей-Люссака.

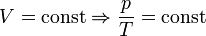— закон Шарля (второй закон Гей-Люссака, 1808 г.).А в форме пропорции этот закон удобен для расчёта перевода газа из одного состояния в другое. С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа.

Смеси газов. В практической деятельности чаще всего имеют дело не с однородными газами, а с их смесями: воздух, продукты сгорания топлива, горючие газовые смеси и т.п.. Поэтому в теплотехнике газовые смеси имеют важное значение. В объеме, занимаемом газовой смесью, каждый газ, входящий в эту смесь, ведет себя так же, как он вел бы себя при отсутствии других составляющих смеси: распространяется по всему объему; создает давление (парциальное), определяемое температурой и объемом на единицу его массы; имеет температуру смеси. Смесь идеальных газов представляет собой идеальный газ, для которого справедливы законы и полученные для идеальных газов зависимости.

Для идеального газа давление определяется выражением (4.1)

Количество молекул, входящих в данную смесь газов, равно сумме молекул газов, составляющих смесь

(4.63)

Произведение mw²=2αT пропорционально абсолютной температуре газа, а поскольку все газы, входящие в смесь, имеют одинаковую температуру, то справедливо равенство

(4.64)

(4.65)

В соответствии с выражениями (4.63) и (4.64) давление для смеси газов можно представить в виде суммы

где P_i- парциальные давления газов, составляющих смесь.

Уравнение (4.65) представляет математическое выражение закона Дальтона (1807 г.), в соответствии с которым, давление газовой смеси равно сумме парциальных давлений газов, входящих в смесь. Парциальное давление это давление, которое создает один из газов, составляющих смесь, при температуре смеси в случае заполнения им всего объема смеси. Парциальное давление это реальносуществующая величина, поскольку каждый отдельный газ в смеси имеет температуру смеси и занимает весь объем смеси. Парциальное давление можно определить из уравнения Менделеева - Клапейрона

(4.66)

где V_СМ - объем, занимаемый всей смесью газов,
m_i - масса отдельного газа, входящего в смесь,
R_i - газовая постоянная отдельного газа,
T_СМ - температура смеси газов.

2. Основное уравнение молекулярно-кинетической теории идеального газа и следствия из него.

. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения).

Вывод основного уравнения мкт[править | править исходный текст]

Пусть имеется частиц массой в некотором кубическом сосуде.

Так как молекулы движутся хаотически, то события, состоящие в движении в одном из шести направлений пространства, совпадающих с осями декартовой системы координат, равновероятностны.

Поэтому, в каждом из этих направлении движется 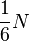частиц.

Пусть все частицы обладают одинаковой скоростью .

Каждая из частиц, сталкивающихся со стенкой, передаёт ей импульс .

Если площадь стенки , а концентрация - , то количество частиц, сталкивающихся со стенкой за время равно .

Так как , а - суммарная сила взаимодействия частиц со стенкой, то подставив соответствующие значения получим , так как , то

 

3. Закон Максвелла для распределения молекул идеального газа по скоростям. Расчёт наиболее вероятной скорости.

При выводе основного уравнения молекулярно-кинетической теории молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направлении в среднем движется одинаковое число молекул.

По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой m₀ в газе, находящемся в состоянии равновесия при Т = const, остается постоянной и равной <v_кв> 3kT/mÖ=₀. Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.

При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN (v)/N, скорости которых лежат в интервале от v до v+dv, т. е.откуда f(v)=dN(v)/Ndv

Применяя методы теории вероятностей, Максвелл нашел функцию f(v) — закон для распределения молекул идеального газа по скоростям:

Из (44.1) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т).

График функции (44.1) приведен на рис. 65. Так как при возрастании v множитель 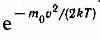уменьшается быстрее, чем растет множитель v², то функция f(v), начинаясь от нуля, достигает максимума при v_в и затем асимптотически стремится к нулю. Кривая несимметрична относительно v_в. Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь более светлой полоски на рис. 65. Площадь, ограниченная кривой распределения

и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки

Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти продифференцировав выражение (44.1) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума выражения f(v):

Значения v= 0и v=¥ соответствуют минимумам выражения (44.1), а значение v, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость v_в:

Из формулы (44.2) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис. 66) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.

Средняя скорость молекулы <v> (средняя арифметическая скорость)

определяется по формуле

Подставляя сюда f(v) и интегрируя, получим

Скорости, характеризующие состояние газа: 1) наиболее вероятная v_в2RT/М; 2) средняяÖ= <v>М)=1,13vp8RT/(Ö=_в; 3) средняя квадратичная <v_кв> 3Ö= RT/М = 1,22v_в (рис.65).

Исходя из распределения молекул по скоростям

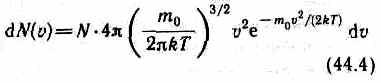
. Для этого перейдем от переменнойeможно найти распределение молекул газа по значениям кинетической энергии v =meк переменной ₀v²/2. Подставив в (44.4) v //me (2Ö=₀ и

dv=(2m₀)e^-1/2, получим ed

.e+de до e) — число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от e до e+de

Таким образом, функция распределения молекул по энергиями теплового движения

Средняя кинетическая энергия <e> молекулы идеального газа

т. е. получили результат, совпадающий с формулой (43.8).

4. Барометрическая формула. Распределение Больцмана.

При рассмотрении закона распределения Максвелла предполагалось, что молекулы равномерно распределяются по всему объему сосуда, что справедливо, если объем сосуда небольшой.

Для больших объемов равномерность распределения молекул по объему нарушается из-за действия силы тяжести, вследствие чего плот­ность, а следовательно, и число молекул в единице объема будут неодинаковым.

Рассмотрим молекулы газа, находящегося в поле тяготения Земли.

Выясним зависимость давления атмосферы от высоты над поверхно­стью Земли. Допустим, на поверхности Земли (h = 0) давление атмосфе­ры P₀. На высоте h оно равно P. При увеличении высоты на dh давление уменьшится на dP:

dP = - ρgdh (9.49)

[ρ — плотность воздуха на данной высоте, ρ = mn₀, где m — масса моле­кулы, n₀ — концентрация молекул].

Используя соотношение P = n₀kТ, получаем

(9.50)

Полагая, что на некоторой высоте h Т = соnst, g = соnst, разделяя пе­ременные, интегрируем выражение (9.50):

,

Получаем

(9.51) — барометрическая формула. Барометрическая формула показывает зависимость давления газа от высоты над поверхностью Земли.

Если учесть, что концентрация молекул воздуха в атмосфере определяет дав­ление, то формулу (9.51) можно записать в виде

(9.52)

Из формулы (9.52) следует, что с понижением температуры число частиц на высоте, отличной от нуля, убывает и при Т = 0К обращается в нуль, т. е. при 0К все молекулы расположились бы на земной поверх­ности.

Так как потенциальная энергия молекул на различной высоте раз­лична и на высоте h определяется по формуле где Е_П = mgh, то [см.

(9.53)

— закон Больцмана, показывающий распределение участвующих в теп­ловом движении молекул в потенциальном поле сил, в частности в поле силы тяжести.

5. Явление переноса: теплопроводность, диффузия, внутреннее трение. Законы Фурье, Фика, Ньютона.

1. Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное взаимопроникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел. Диффузия сводится к переносу массы, возникает и продолжается до тех пор, пока на границе соприкосновения двух сред градиент плотности отличен от нуля.

Градиент плотности вдоль выбранной оси х, перпендикулярной плоскости соприкосновения двух сред, обозначается как и показывает как быстро изменяется величина плотности от точки к точке вдоль оси х.

Количественно явление диффузии подчиняется закону Фика:

,

где – плотность потока массы, то есть величина, определяемая массой газа, диффундирующего через единичную площадку S в единицу времени,

– градиент плотности газа в направлении x, перпендикулярном выбранной площадке S,

D – коэффициент диффузии.

Знак минус в приведенной формуле означает, что перенос массы происходит в направлении убывания плотности.

Согласно молекулярно-кинетической теории идеального газа, коэффициент D:

,

где – средняя скорость теплового движения молекул,

–средняя длина свободного пробега молекул.

2. Теплопроводность. Если в одной области газа температура больше,чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, то есть процесс выравнивания температуры. Этот процесс переноса энергии, называемый теплопроводностью, возникает и продолжается до тех пор, пока на границе соприкосновения двух частей газа градиент температуры отличен от нуля.

Градиент температуры Т газа вдоль выбранной оси х, перпендикулярной плоскости соприкосновения двух частей газа, имеющих различную температуру, обозначается как и показывает как быстро изменяется температура газа от точки к точке вдоль оси х.

Количественно теплопроводность подчиняется закону Фурье:

,

где – плотность теплового потока – величина, определяемая энергией, переносимой в форме теплоты через единичную площадку S в единицу времени,

–градиент температуры в направлении x, перпендикулярном выбранной площадке S,

– коэффициент теплопроводности.

Знак минус в приведенной формуле означает, что при теплопроводности энергия переносится в направлении убывания температуры.

Согласно молекулярно-кинетической теории идеального газа, коэффициент теплопроводности определяется следующим образом:

,

где – удельная теплоемкость газа при изохорном процессе (количество теплоты, необходимое для изохорного нагревания1 кг газа на 1 К),

–плотность газа,

–средняя скорость теплового движения молекул,

–средняя длина свободного пробега молекул.

3. Вязкость. Вязкость это свойство жидкости или газа, обусловленное внутренним трением между соприкасающимися параллельными слоями жидкости или газа, движущимися с различными скоростями. В результате, импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Другими словами, внутреннее трение приводит к переносу импульса от одного движущегося слоя жидкости или газа к другому соприкасающемуся с ним слою.

Количественно сила внутреннего трения между двумя соприкасающимися слоями жидкости или газа подчиняется закону Ньютона:

,

где h – коэффициент динамической вязкости,

–градиент скорости, показывающий быстроту изменения скорости течения жидкости или газа от слоя к слою в направлении х, перпендикулярном направлению движения слоев,

S – площадь соприкосновения слоев жидкости или газа, на которые действует сила внутреннего трения F.

Закон Ньютона для внутреннего трения можно представить в виде:

,

где – плотность потока импульса – величина, определяемая импульсом, переносимым в единицу времени через единичную площадку S соприкосновения слоев жидкости или газа в направлении оси х, перпендикулярном направлению движения слоев жидкости или газа.

Знак минус в приведенной формуле означает, что импульс переносится от слоя к слою жидкости (газа) в направлении убывания скорости их движения.

Согласно молекулярно-кинетической теории идеального газа, коэффициент динамической вязкости идеального газа h определяется следующим образом:

,

где – плотность газа,

–средняя скорость теплового движения молекул,

–средняя длина свободного пробега молекул.

6. Число степеней свободы газовых молекул. Распределение энергии по степеням свободы. Внутренняя энергия идеального газа.

Числом степеней свободы называется наименьшее число независимых координат, которое необходимо ввести, чтобы определить положение тела в пространстве. – число степеней свободы.

Рассмотрим одноатомный газ. Молекулу такого газа можно считать материальной точкой, положение материальной точки (рис. 11.1) в пространстве определяется тремя координатами.

Молекула может двигаться в трех направлениях (рис. 11.2).

Рис. 11.1	Рис. 11.2

Следовательно, обладает тремя поступательными степенями свободы.

Молекула – материальная точка.

Энергии вращательного движения , т.к. момент инерции материальной точки относительно оси, проходящей через точку равен нулю

Для молекулы одноатомного газа число степеней свободы .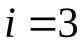

Рассмотрим двухатомный газ. В двухатомной молекуле каждый атом принимается за материальную точку и считается, что атомы жёстко связаны между собой, это гантельная модель двухатомной молекулы. Двухатомная жестко связанная молекула (совокупность двух материальных точек, связанных недеформируемой связью), рис. 11.3.

Положение центра масс молекулы задаётся тремя координатами, (рис. 11.4) это три степени свободы, они определяют поступательное движение молекулы. Но молекула может совершать и вращательные движения вокруг осей и , это ещё две степени свободы, определяющие вращение молекулы. Вращение молекулы вокруг оси невозможно, т.к. материальные точки не могут вращаться вокруг оси, проходящей через эти точки.

Рис. 11.3	Рис. 11.4

Для молекулы двухатомного газа число степеней свободы .

Рассмотрим трёхатомный газ. Модель молекулы – три атома (материальные точки), жёстко связанные между собой (рис. 11.5).

Трёхатомная молекула – жестко связанная молекула.

Рис. 11.5

Молекула обладает 3 поступательными и 3 вращательными степенями свободы. i = i поступат + i вращат = 6.

Для молекулы трёхатомного газа число степеней свободы .

Для многоатомной молекулы число степеней свободы .

Для реальных молекул, не обладающих жёсткими связями между атомами, необходимо учитывать также степени свободы колебательного движения, тогда число степеней свободы реальной молекулы равно

i = i _{поступат} + i _{вращат.}+ i _колеб. (11.1)