Самоаффинные фрактальные множества II. Размерности длины и поверхности
Введение
Представляется соблазнительным попытаться измерить длину кривой с помощью измерительного циркуля, последовательно уменьшая его раствор, или измерить площадь поверхности с помощью все более и более мелкой триангуляции. Для обычных кривых такая процедура дает хороший результат. В то же время известно, что уже для обычных поверхностей (например, для цилиндра) возникают аномалии; основная аномалия проявляется в так называемом парадоксе площадей Шварца, который заслуживает широкой известности и будет обсуждаться ниже. Для самоподобных кривых эта процедура снова приводит к фрактальной размерности. Попытаемся использовать такую процедуру для самоаффинных фракталов и покажем, что размерности, к которым она приводит, отличаются от массовой и клеточной размерностей.
Измерение длины самоаффинных фрактальных кривых, являющихся графиками функций
2.1. Измерение длины с использованием «сосиски» Минковского дает локальную и глобальную размерности, совпадающие с DML и DMG
Следуя Минковскому и Булигану, определим приближенную длину кривой В( ), используя «сосиску» Минковского, содержащую все точки на расстоянии, меньшем чем
), используя «сосиску» Минковского, содержащую все точки на расстоянии, меньшем чем  , от данной точки кривой. Для обычной спрямляемой кривой и при
, от данной точки кривой. Для обычной спрямляемой кривой и при  << 1 В(
<< 1 В( ) = (2
) = (2  )-1 (площадь сосиски). Для самоподобной кривой (см. [2], с. 36) B(
)-1 (площадь сосиски). Для самоподобной кривой (см. [2], с. 36) B( )~
)~  1-D, для самоаффинной кривой площадь сосиски при малых
1-D, для самоаффинной кривой площадь сосиски при малых  ведет себя как N (
ведет себя как N ( )
)  -2 ~
-2 ~  H, и поэтому локальная размерность равна 2— Н. Глобальная размерность равна 1. Оба этих значения встречались в части I данной статьи.
H, и поэтому локальная размерность равна 2— Н. Глобальная размерность равна 1. Оба этих значения встречались в части I данной статьи.
2.2. Нахождение длины с помощью измерительного циркуля при фиксации последнего выхода кривой дает локальную и глобальную размерности, совпадающие с DML и DMG
В одном из многих методов нахождения длины спрямляемой кривой используется измерительный циркуль, перемещающийся вдоль кривой. На кривой могут быть узлы, т. е. кратные точки произвольного порядка; достаточно, чтобы точки кривой были упорядочены, например «во времени». Начнем с исходной точки р0. Первая точка Р1 будет первым выходом кривой из круга с центром в ро и радиусом  и т. д. Если обозначить через L(
и т. д. Если обозначить через L( ) длину возникающей ломаной линии, приближенно описывающей нашу кривую, то длина кривой будет lim
) длину возникающей ломаной линии, приближенно описывающей нашу кривую, то длина кривой будет lim 
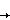 0 L(
0 L( ).
).
Можно выбрать в качестве P1 точку последнего, а не первого выхода вдоль кривой. И можно также двигаться назад.
Для самоподобной кривой находим L( ) ~
) ~  1-D, и снова по желанию можно отмечать либо первый, либо последний выход кривой.
1-D, и снова по желанию можно отмечать либо первый, либо последний выход кривой.
Для наших самоаффинных кривых ситуация оказывается совершенно иная. Кроме локальной размерности при 
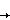 0 имеется также глобальная размерность, которая, как мы увидим, равна 1. И локальная размерность, полученная при помощи измерительного циркуля, имеет два совершенно различных значения, одно для последних, а другое для первых выходов. Прежде чем двигаться дальше, заметим, что для самоподобных функций рассмотрение становится проще (а результаты не меняются), если круг с центром в точке Pk заменить квадратом.
0 имеется также глобальная размерность, которая, как мы увидим, равна 1. И локальная размерность, полученная при помощи измерительного циркуля, имеет два совершенно различных значения, одно для последних, а другое для первых выходов. Прежде чем двигаться дальше, заметим, что для самоподобных функций рассмотрение становится проще (а результаты не меняются), если круг с центром в точке Pk заменить квадратом.
Если воспользоваться этим обстоятельством, то рассмотрение последних выходов становится простым. Покроем нашу кривую (b''k)2-H квадратами со стороной (b")k< <1; это дает D>2—H. Далее добавим кольцо из 8 таких же квадратов вокруг каждой ячейки и тем самым увеличим сторону втрое. Ясно, что (b"k)2-H шагов циркуля с раствором 3(b")-k достаточно, чтобы пройти вдоль кривой, поэтому размерность, полученная с помощью измерительного циркуля, меньше 2— Н. Следовательно, она равна 2-H.
2.3. Нахождение длины с помощью измерительного циркуля при фиксации первых выходов дает «аномальные размерности». Локальное значение размерности при малых  равно 1/Н. Эта величина совпадает с фрактальной размерностью фрактального следа, связанного с функцией. Для больших п размерность равна 1
равно 1/Н. Эта величина совпадает с фрактальной размерностью фрактального следа, связанного с функцией. Для больших п размерность равна 1
В этом разделе приведены результаты, полученные в работе [I].
При  >> t с (например, когда единица измерения ВH достаточно мала) график по сути дела близок к горизонтальной линии. При передвижении измерительного циркуля вдоль кривой
>> t с (например, когда единица измерения ВH достаточно мала) график по сути дела близок к горизонтальной линии. При передвижении измерительного циркуля вдоль кривой
он в основном остается параллельным оси t, и L( ) слабо меняется с изменением
) слабо меняется с изменением  . Если считать, что L(
. Если считать, что L( )~
)~  1-D, тогда то обстоятельство, что L(
1-D, тогда то обстоятельство, что L( ) является константой, дает для глобальной размерности значение 1 независимо от Н.
) является константой, дает для глобальной размерности значение 1 независимо от Н.
Если, наоборот,  << tc (например, когда единица измерения ВH велика), то ситуация оказываетя иной: измеритель, передвигающийся вдоль кривой, в основном остается параллельным оси В. В результате получаем размерность, равную 1 /Н.
<< tc (например, когда единица измерения ВH велика), то ситуация оказываетя иной: измеритель, передвигающийся вдоль кривой, в основном остается параллельным оси В. В результате получаем размерность, равную 1 /Н.
Это чрезвычайно странное значение может превышать 2 и является аномальным вдвойне: оно противоречит значению 2- Н, которое получалось при других локальных определениях фрактальной размерности. С другой стороны, те, кто знакомы с фрактальным броуновским движением, могут отождествить 1/Н с фрактальной размерностью следа (в некотором E-мерном евклидовом пространстве RE при Е > 1/Н) движения, для которого координаты Е представляют собой независимые реализации Вн(t).
В этом случае попытка использовать необычный путь для измерения фрактальной размерности для одного множества в действительности заканчивается измерением значения, которое все пути дают для некоторого другого множества.