Триангуляция обычных поверхностей оказывается делом гораздо более сложным, чем можно было бы ожидать. В частности, в конце XIX в. Герман Амандус Шварц показал, что для случая цилиндра единичного радиуса и единичной высоты безобидный на первый взгляд метод триангуляции может дать для площади боковой поверхности любую величину: от истинного значения 2  до бесконечности!
до бесконечности!
Поступим следующим образом: разделим цилиндр по высоте на п слоев плоскостями z =р/п (р— целое число больше нуля) и выделим на окружностях с четным номером уровня точки 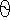 = (2q+1)
= (2q+1)  /m (q—целое), а на окружностях с нечетным номером уровня — точки
/m (q—целое), а на окружностях с нечетным номером уровня — точки 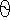 = 2q
= 2q  /m. Соединим каждую точку (z,
/m. Соединим каждую точку (z, 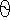 ) с точками (z
) с точками (z  1 /n,
1 /n, 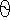

 /m). Таким образом, боковая поверхность единичного цилиндра приближенно представлена 2mn равными треугольниками. Теперь, чтобы получить истинную площадь, кажется естественным сложить площади этих треугольников и затем произвольным образом независимо устремить n
/m). Таким образом, боковая поверхность единичного цилиндра приближенно представлена 2mn равными треугольниками. Теперь, чтобы получить истинную площадь, кажется естественным сложить площади этих треугольников и затем произвольным образом независимо устремить n 
 , m
, m 
 .
.
Прямое вычисление показывает, что для больших m эта площадь приближенно равна 2  sqrt([1 + (
sqrt([1 + ( 4/4)n2/m4]). Если т
4/4)n2/m4]). Если т 
 , но n/m2
, но n/m2  0, то это приближенное выражение действительно сходится к величине 2
0, то это приближенное выражение действительно сходится к величине 2  . Однако, если т
. Однако, если т 
 и п =
и п =  m2 (
m2 ( = const > 0), мы получим произвольное конечное значение, превышающее 2
= const > 0), мы получим произвольное конечное значение, превышающее 2  ! И мы можем сказать, кроме того, что, выбирая п ~ m
! И мы можем сказать, кроме того, что, выбирая п ~ m  ,
,  > 2, можно добиться, чтобы приближенное значение площади возрастало как произвольная степень либо 1 /т, либо 1 /п, либо площади треугольника, пропорциональной 1 /тп. Цилиндр оказывается похожим на фрактал! Его площадь неограниченно возрастает при таком способе измерения.
> 2, можно добиться, чтобы приближенное значение площади возрастало как произвольная степень либо 1 /т, либо 1 /п, либо площади треугольника, пропорциональной 1 /тп. Цилиндр оказывается похожим на фрактал! Его площадь неограниченно возрастает при таком способе измерения.
Причиной такого поведения является следующее обстоятельство: при переходе к пределу т/п 
 мы используем треугольники, которые а) становятся все более и более узкими, т. е. имеют хотя бы один угол, стремящийся к нулю, и б) лежат в плоскостях, стремящихся стать перпендикулярно боковой поверхности цилиндра. При этом возникающая поверхность становится все более и более «волнистой» и все больше удаляется от истинной поверхности.
мы используем треугольники, которые а) становятся все более и более узкими, т. е. имеют хотя бы один угол, стремящийся к нулю, и б) лежат в плоскостях, стремящихся стать перпендикулярно боковой поверхности цилиндра. При этом возникающая поверхность становится все более и более «волнистой» и все больше удаляется от истинной поверхности.
Реакция прагматика была бы следующей — избегать узких треугольников. Ответ математика: «парадокс площадей Шварца» относился к числу проблем, способствовавших.развитию современной математики. В частности, этот парадокс стимулировал Минковского дать корректные определения длины и площади через объемы все более тонких «сосисок» Минковского для кривых и все более тонких «шарфов» Минковского для поверхностей. Эти множества состоят из всех точек внутри  -окрестности некоторой точки кривой или поверхности. Так, Минковский определяет площадь обычной поверхности как
-окрестности некоторой точки кривой или поверхности. Так, Минковский определяет площадь обычной поверхности как
lim (1/2  ) x (объем ) x (объем  -шарфа). -шарфа).
| ||
  0 0
|
В отличие от треугольников все интервалы подобны друг другу, и поэтому для обычной кривой в плоскости аналога парадокса Шварца не существует. Его не существует также и для самоподобных фрактальных кривых; действительно, в [2] отмечено, что измерения длины с переменной точностью е могут быть проведены многими различными путями, но во всех случаях длина меняется по одному и тому же закону: пропорционально е1-0. Но для самоаффинных кривых, как показано в разд. 2.1—2.3, ситуация более сложная. Здесь длина растет как  1-D, но D = DBL при подходе Минковского и D = DCL > DBL при использовании измерительного циркуля. Может ли размерность D принимать значения, отличающиеся от этих двух величин?
1-D, но D = DBL при подходе Минковского и D = DCL > DBL при использовании измерительного циркуля. Может ли размерность D принимать значения, отличающиеся от этих двух величин?