Формулы для расчета напряжений в дисках

Для определения надежности элементов ротора турбоустановки необходимо знать напряжения и деформации, возникающие в процессе их работы. Для определения напряженного и деформированного состояния используются методы теории упругости, в которой предполагается, что между напряжениями и деформациями существует однозначная связь (закон упругости). Но в реальных конструкциях эта связь не однозначна и приходится пользоваться элементами теории пластичности, где выбирается гипотеза о связи между компонентами напряжений и деформаций. Вместе с тем данные теории не могут предсказать условий разрушения материалов. Поэтому дополнительно используются гипотезы прочности. При высокой температуре (около половины абсолютной температуры плавления) проявляются особые свойства материалов, называемые ползучестью. Теория ползучести позволяет помимо определения напряжений и деформаций определить время, в течение которого конструкция будет работоспособной.

Диски роторов нагружены центробежными силами, силами от разности давлений на боковых стенках тела диска, окружными усилиями в лопаточном аппарате, силами, возникающими при посадке диска на вал с натягом, а также температурными напряжениями, если температура диска неодинакова. Обычно условия работы дисков турбинных ступеней активного типа определяют значимость только центробежных сил и сил в месте посадки их на вал. (рис. 26.9). Здесь радиус r₂ равен радиусу, на котором заканчиваются пазы под хвостовики лопаток. Тогда радиальные напряжения в полотне диска:

, (26.11)

где R_цл – центробежная сила от действия лопаток и бандажа; R_цоб – центробежная сила части обода, расположенной за пределами радиуса r₂; z₂ – ширина обода диска. Кроме того, при посадке диска на вал с натягом на поверхности радиусом r₁ возникают контактные напряжения s_r1 (рис. 26.9). Допустим, что напряжения по толщине диска не меняются. Обозначим нормальные напряжения по меридиональным поверхностям s_t, а на цилиндрических - s_r. Рассмотрим равновесие его бесконечно малого элемента по схеме рис. 26.10, в центре тяжести которого приложена центробежная сила dС (вывод вне экзаменационной программы).

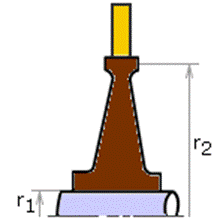
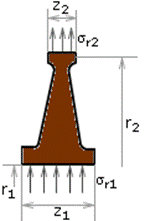
Рис. 26.9. Схема нагружения диска

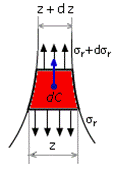
Рис. 26.10. Схема усилий и напряжений в диске

Формулы для определения радиальных и тангенциальных напряжений в диске постоянной толщины с отверстием:

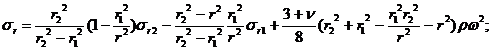(26.12)

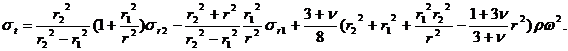(26.13)

Здесь ν – коэффициентПуассона (отношение относительной поперечной деформации к относительной продольной).

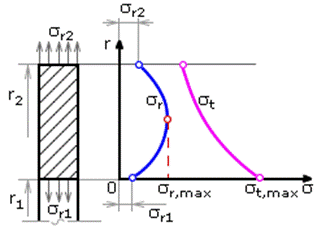
Распределение соответствующих напряжений в диске показано на рис. 26.11, а. Радиальные напряжения имеют максимум между радиусами r₁ и r₂. Тангенциальные напряжения максимальны на поверхности отверстия и всюду растягивающие. В диске, посаженном на вал с натягом, на расточке имеют место сжимающие радиальные напряжения. В этом случае s_r1<0.

Формулы определения напряжений для диска без отверстия имеют следующий вид:

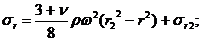(26.14)

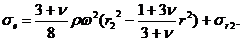(26.15)

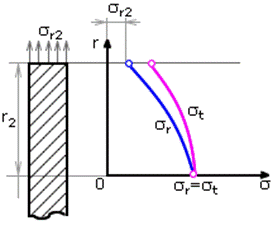
В сплошном диске все напряжения растягивающие (рис. 26.11, б).

А) б)

Рис. 26.11. Распределение напряжений в плоском диске с отверстием (а) и без отверстия (б)

Обычно диски паровых турбин имеют сложную форму, отличную от постоянного профиля (рис. 26.12).

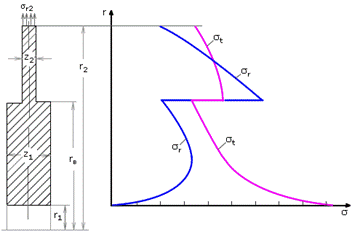
Рис. 26.12. Распределение напряжений в диске сложной формы

В случаях, если форма профиля диска приближена к конической, гиперболической или равного сопротивления, то диск произвольного профиля заменяют ступенчатым, состоящим из колец постоянной толщины. Тогда при переходе от одного участка постоянной толщины к другому радиальные и тангенциальные напряжения изменяются скачком на границе между участками (рис. 26.12). Например, для радиальных напряжений связь в скачке осуществляется из соотношения: s_r(n+1)(z_n+1)=s_rnz_n, а для тангенциальных .