Постановка задачи. Пусть корень ξ уравнения 
отделен на отрезке [ a, b ], причем производные 
и 
непрерывны и сохраняют постоянные знаки на отрезке [ a, b ]. Найти с точностью ε корень уравнения .
В основе метода Ньютона лежит разложение функции 
в ряд Тейлора. Пусть имеем какое-нибудь n – е приближение xn для искомого корня ξ, т. е.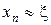 
. Положим, что 
, где hn – малая величина. Запишем формулу Тейлора для многочлена Pn (x) степени не выше n, значение которого в точке 
равно значению функции в этой точке:
.
Так как 
, то для 
имеем
.
Поскольку 
, то отбрасывая ввиду малости члены, содержащие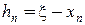 
во второй и более степенях, находим
,
откуда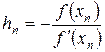 
Внесем эту поправку в формулу . Получим следующее (по порядку) приближение корня:
.
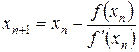Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой 
касательной, проведенной в некоторой точке этой дуги. Например, выберем в качестве начального приближения 
границу b отрезка [ a, b ] существования корня. Причем, в этой точке 
и 
. Проведем касательную к кривой 
в точке 
(рис. 3, а). Точку 
пересечения этой касательной с осью абсцисс возьмем в качестве следующего приближения корня ξ. Из геометрических соображений при рассмотрении треугольника 
легко установить, что
.
В точке 
проводим новую касательную к кривой . Точка пересечения этой касательной с осью абсцисс дает новое приближение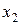 
для уточняемого корня ξ:
.
Таким образом, для n +1 – го приближения имеем
.
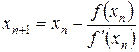Если в нашем примере в качестве нулевого приближения 
положить значение левой границы [ a, b ], т. е.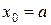 
, где выполняется неравенство 
, то проведя касательную в точке 
, мы получим точку 
, лежащую вне отрезка [ a, b ] существования искомого корня ξ. При таком выборе начального приближения метод Ньютона не обладает сходимостью. Поэтому при применении метода Ньютона в качестве нулевого приближения для уточняемого корня выбирают тот конец интервала [ a, b ], для которого выполняется неравенство 
.
 |
Вычисление на ЭВМ корня уравнения по методу Ньютона может быть произведено по алгоритму, схема которого приведена на рис. 3, г. 3десь блоки 4-6 описывают действия, связанные с выбором начального приближения для уточняемого корня. Блоки 7-9 образуют цикл по вычислению корня с заданной точностью ε.
Отметим два момента, связанных с применением метода Ньютона.
1. В общем случае совпадение с точностью ε двух последовательных приближений xn -1 и xn еще не является гарантией того, что с той же точностью совпадает xn с точным значением ξ корня (рис. 3,б).
2. Для функций с пологими или параллельными оси абсцисс участками точка пересечения касательной с осью абсцисс может выйти за пределы отрезка [ a, b ], содержащего корень (рис. 3,в). В этом случае метод Ньютона не обладает сходимостью.
С учетом этих моментов рекомендуется выбирать достаточно тесные границы отрезка [ a, b ] существования корня. В ряде случаев вводится дополнительный критерий окончания процесса уточнения корня – условие равенства функции 
в точке xn достаточно малой величине δ, т. е.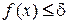 
, где δ составляет, например, 10-6.