Лекция 8
2018/2019 уч. г.
Тема 10. Приближенные методы решения дифференциальных уравнений с частными производными
Введение. Основные сведения об алгебраических линиях и их порядке.
1. Основные понятия о дифференциальных уравнений с частными производными, их классификация.
2. Начальные и граничные условия.
3. Пример постановки краевой задачи при моделировании объектов технологической системы.
4. Методы решения краевых задач. Этапы решения краевой задачи разностным методом.
5. Пример построения разностной схемы краевой задачи.
Литература.
1. Данилина Н.И. и др. Вычислительная математика: Учеб. пособие для техникумов. – М.: Высш. шк., 1985, 472 с.
2. Копченова Н.Н., Марон И.А. Вычислительная математика в примерах и задачах. Учеб. пособие. – СПб.: Изд-во «Лань», 2008, 368 с.
3. Выгодский М.Я. Справочник по высшей математике. – М.: Изд-во «Наука», 1969, 872 с.
4. Турчак Л.И., Плотников П.В. Основы численных методов: Учеб. пособие. – М.: ФИЗМАТЛИТ, 2005, 304 с.
Введение. Основные сведения об алгебраических линиях
И их порядке
В высшей математике уравнение с двумя неизвестными x, y вида
 , (В.1)
, (В.1)
в котором, по крайней мере, одна из величин A, B, C не равна нулю называется алгебраическим уравнением второй степени.
Аналогично записываются алгебраические уравнения третьей, четвертой и т. д степеней. Величины A, B, C и т. п. (в том числе F – свободный член) называются коэффициентами алгебраического уравнения.
Линия L, представляемая в декартовой системе координат уравнением n –й степени, называется алгебраической линией n – го порядка.
Уравнение (В.1) описывает линию второго порядка. Рассмотрим возможные виды линий второго порядка и их соответствующие уравнения.
1.  Окружность. Пусть начало координат совпадает с центром окружности радиусом R = a (рис. 1), то окружность представляется уравнением
Окружность. Пусть начало координат совпадает с центром окружности радиусом R = a (рис. 1), то окружность представляется уравнением
 . (В.2)
. (В.2)
Это алгебраическое уравнение второй степени (1), в котором  , B = 0,
, B = 0, 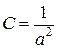 , D =0, E = 0, F = - 1.
, D =0, E = 0, F = - 1.
2. Эллипс. В случае если  , B = 0,
, B = 0,  , D =0, E = 0, F = - 1, т. е. уравнение (В.1) имеет вид
, D =0, E = 0, F = - 1, т. е. уравнение (В.1) имеет вид
 , (В.3)
, (В.3)
 то такое уравнение описывает линию второго порядка, называемую эллипсом (рис. 2). В нем величины a, b - называются большой и малой полуосями эллипса. Между ними имеет место соотношение
то такое уравнение описывает линию второго порядка, называемую эллипсом (рис. 2). В нем величины a, b - называются большой и малой полуосями эллипса. Между ними имеет место соотношение
 ,
,
где e – называется эксцентриситетом эллипса,  .
.
3. Гипербола. В случае  , B = 0,
, B = 0,  , D =0, E = 0, F = - 1, т. е. уравнение (В.1) имеет вид
, D =0, E = 0, F = - 1, т. е. уравнение (В.1) имеет вид
 , (В.4)
, (В.4)
 то такое уравнение описывает линию второго порядка, называемую гиперболой (рис. 3).
то такое уравнение описывает линию второго порядка, называемую гиперболой (рис. 3).
Гипербола представляет собой геометрическое место точек M, разность расстояний которых до двух данных точек F’ и F имеет одно и то же абсолютное значение
 .
.
Точки F’ и F называются фокусами гиперболы, расстояние F’F – фокусным расстоянием; оно обозначается через 2 c:
F’F = 2 c.
 В уравнении (В.4) величина b составляет
В уравнении (В.4) величина b составляет  , так что
, так что  .
.
4. Парабола. Параболой называют геометрическое место точек M, равноудаленных от данной точки F и данной прямой PQ:
 .
.
Точка F называется фокусом, а прямая PQ директрисой параболы. Расстояние  от фокуса до директрисы называется параметром параболы.
от фокуса до директрисы называется параметром параболы.
При расположении параболы в декартовой системе координат так, как приведено на рис. 4, в уравнении (В.1) будем иметь 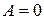 , B = 0,
, B = 0,  , D =-2 p, E = 0, F = 0 и, следовательно, парабола описывается уравнением вида
, D =-2 p, E = 0, F = 0 и, следовательно, парабола описывается уравнением вида
 . (В.5)
. (В.5)
Приведенные уравнения (В.2)-(В.5) окружности, эллипса, гиперболы и параболы называются каноническими (типовыми) уравнениями этих линий. Является естественным, что если эти геометрические линии будут располагаться в декартовой системе как-то иначе, то они будут описаны в виде уравнения (В.1). Вместе с тем путем изменения расположения осей координат (их поворота и последующего переноса начала исходной системы координат) можем получить уравнение той или иной линии в канонической форме, но уже в новой системе координат.
Замечание. Если в уравнении (В.1) A =0, B =0, C =0, то оно является алгебраическим уравнением первой степени и представляет прямую линию в декартовой системе координат.
Основные понятия о дифференциальных уравнений
с частными производными, их классификация
Дифференциальные уравнения с частными производными – это уравнения, содержащие неизвестную функцию нескольких переменных и ее частных производных.
Например,
 ;
;  ;
;
 ;
;  ,
,
где x, y, z – независимые переменные, u = u (x, y) - неизвестная функция в первых трех уравнениях и u = u (x, y, z) - в последнем.
Как и для обыкновенных дифференциальных уравнений, порядок уравнения с частными производными определяется наивысшим порядком входящей в него производной. В приведенных примерах первые два уравнения являются уравнениями первого порядка, остальные – второго.
Необходимость решения таких уравнений возникает в задачах гидродинамики, механики сплошных тел, тепло- и массопереноса и многих других областей знаний. Например, напряжения в валах, балках при нагружении их крутящими моментами определяется функцией ψ(x, y), являющейся решением уравнения
 .
.
Наиболее часто в инженерной практике возникает необходимость решения дифференциальных уравнений второго порядка. В случае неизвестной функции u (x, y) двух независимых переменных x и y оно имеет следующий общий вид:
 , (1)
, (1)
где u = u (x, y) – неизвестная функция, которую нужно найти; a, b, c, d, e, f – коэффициенты уравнения, g – свободный член.
В самом общем случае коэффициенты a, b, c, d, e, f и свободный член уравнения g могут представлять собой функции от переменных x, y и неизвестной функции u (x, y). В связи с этим различают:
- дифференциальные уравнения с постоянными коэффициентами;
- линейные уравнения, если g линейно зависит от u, а коэффициенты зависят только от x, y;
- квазилинейные уравнения, если g не зависит от u или зависит от u линейно, при этом коэффициенты также являются функциями от u;
- однородное уравнение, если g = 0.
Решением уравнения (1) является любая функция u (x, y), если при подстановке ее в это уравнение обращает его в тождество. Отметим коренное отличие общего решения дифференциального уравнения с частными производными от общего решения обыкновенного дифференциального уравнения.
Известно, что общее решение обыкновенного дифференциального уравнения содержит в себе произвольные постоянные. Число их определяется порядком уравнения. Общее решение обыкновенного дифференциального уравнения первого порядка содержит в себе одну произвольную постоянную, уравнение второго порядка – две и т. д.
Общее решение дифференциального уравнения с частными производными содержит в себе не произвольные постоянные, а произвольные функции. Для уяснения этого рассмотрим несколько примеров дифференциальных уравнений, содержащих неизвестную функцию u (x, y) двух переменных x, y.
Пример 1. Пусть имеем уравнение
 . (2)
. (2)
Ясно, что искомая функция u (x, y) не зависит от x, но может быть любой функцией от y, т. е.
u (x, y) = φ(y). (3)
Действительно, подставляя функцию φ(y) в уравнение (2) вместо u, мы получим тождество. Следовательно, решение (3) уравнения (2) содержит одну произвольную функцию φ(y).
Пример 2. Имеем уравнение с правой частью
 . (4)
. (4)
Является очевидным, что все функции u (x, y), удовлетворяющие уравнению (4), имеют вид
 , (5)
, (5)
где ψ(x) – произвольная функция от x. То, что это так можно проверить подстановкой решения (5) в уравнение (4).
Пример 3. Пусть имеем дифференциальное уравнение второго порядка вида
 . (6)
. (6)
Выполним подстановку
 . (7)
. (7)
Тогда уравнение (6) примет вид
 .
.
Но общим решением уравнения 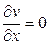 , как показано в примере 1, будет произвольная функция v = f (y). Возвращаясь к подстановке (7), получаем
, как показано в примере 1, будет произвольная функция v = f (y). Возвращаясь к подстановке (7), получаем
 ,
,
т. е. пришли к уравнению (4), которое имеет общее решение (5). Так как в нем f (y) – произвольная функция от y, то и интеграл от нее также является произвольной функцией, которую можем обозначить через φ(y). Таким образом, имеем решение дифференциального уравнения (6) второго порядка, включающее в себя две произвольные функции
 . (8)
. (8)
Подстановкой в исходное уравнение (6) можем убедиться, что полученная функция (8) является его решением.
Л. Эйлер показал, что линейное уравнение вида
 , (9)
, (9)
в котором g линейно зависит от u, а коэффициенты зависят только от x и y, с помощью замены независимых переменных x, y через переменные ξ и η по формулам
 и
и 
может быть приведено к одному из следующих видов:
1. Если дискриминант  , то уравнение (9) после перехода к новым переменным ξ и η принимает вид
, то уравнение (9) после перехода к новым переменным ξ и η принимает вид
 , (10)
, (10)
которое называется уравнением эллиптического типа (вида).
2. Если  , то уравнение (9) примет вид
, то уравнение (9) примет вид
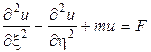 , (11)
, (11)
называемым уравнением гиперболического типа (вида).
3. Если  , то получим
, то получим
 (12)
(12)
- уравнение параболического вида.
В уравнениях (10) - (12) m - постоянное число, F - функция от переменных ξ и η.
Эти наименования уравнений объясняются тем, что при исследовании общего алгебраического уравнения кривых второго порядка
 ,
,
как показано выше во введении, имеем:
- при  алгебраическое уравнение
алгебраическое уравнение  , которое описывает линию второго порядка, называемую эллипсом;
, которое описывает линию второго порядка, называемую эллипсом;
- при  алгебраическое уравнение
алгебраическое уравнение  , которое описывает гиперболу;
, которое описывает гиперболу;
- при  алгебраическое уравнение
алгебраическое уравнение  , которое описывает параболу.
, которое описывает параболу.