Глава 6. Эффективность применения системы СПУ
Для введения объективных критериев оценки эффективности управления объектом (Проектными исследованиями, опытными разработками, капитальными ремонтами оборудования, строительными и другими объектами) по системе СПУ разработана ГОСИНТИ система коэффициентов, основанная на анализе хода работ, входящих в состав комплексного сетевого графика,
В качестве этих коэффициентов принимаются динамика изменения критического пути по времени в процессе выполнения комплекса работ и соответствующее ей изменение резервов времени его событий.
Чтобы определить коэффициенты эффективности управления комплексом работ по системе СПУ, необходимо знать продолжительность критического пути (tкр) и планируемое время выполнения разработки (tпл).
В качестве примера рассмотрим сетевой график, использованный при проведении капитального ремонта технологического оборудования производства диметилтерефталата на Могилев-ском комбинате синтетического волокна.
Графическое изображение динамики хода работ по сетевому графику представлено на рис. 6.1, где по оси ординат отложено планируемое время выполнения комплекса работ в днях, а по оси абсцисс — периоды снятия информации о ходе выполнения работ (календарное время). Динамика хода работ критического пути изображена ломаной линией, а планируемое время — прямой линией, составляющей с осями координат угол 45*.
Начало координат соответствует началу работ по системе СПУ (15 мая). Планируемое время завершения всех ремонтных работ — 30 мая, т.е. срок выполнения ремонта составляет 15 календарных дней. Каждая точка прямой линии (план работ) определяет число дней (абсолютное и календарное), оставшееся по плану до завершения всего комплекса работ.
В каждый момент времени Т по расстоянию между прямой, соответствующей планируемому времени выполнения работ,
и ломаной, означающей величину критического пути, устанавливается величина резервов времени. В зависимости от взаимного расположения этих линий величина резерва может быть либо положительной (ломаная линия проходит под прямой), либо отрицательной (ломаная линия расположена над прямой).
Анализ первоначального варианта сетевого графика показал, что продолжительность критического пути составляет 18 дней (при установленном плане 15 дней), кроме того, на графике имеются два подкритических пути продолжительностью соответственно 17 и 15 дней, резервы времени по критическому и одному подкритическому пути отрицательные.
Руководители и ответственные исполнители провели тщательный анализ и выработали ряд мероприятий по ускорению выполнения исходных работ комплексного сетевого графика. В результате этого в период снятия информации 17 мая было определено, что длина критического пути в течение двух рабочих дней сократилась на 3,5 дня, т.е. отрицательный резерв времени работ критического пути сократился с 3 дней до 1,5 дня, резерв времени двух подкритических путей стал положительным (рис. 6.1).
Последующие периоды снятия информации о ходе проведения ремонтных работ по объекту показывают тенденцию уменьшения величины критического и подкритических путей и сокращение отрицательного резерва времени до нуля, что и показало снятие информации на 21 мая. После 21 мая продолжительность критического пути (
) и плановый срок (
) сравнялись и составили 9 дней (время, оставшееся по плану до завершения всего комплекса работ). Для сокращения срока проведения ремонта было принято решение выполнять работы, лежащие на критическом и подкритическом путях, в три смены и тем самым добиться завершения всего комплекса работ 27 мая, что позволило на 3 дня сократить плановые сроки ремонта.
Таким образом, по относительному положению прямой, соответствующей планируемому сроку выполнения работ, и ломаных, означающих фактическую длительность их выполнения и характеризующих в каждый момент времени величину фактического критического пути (
), можно судить о качестве принимаемых решений и эффективности управления по системе СПУ.
При этом если ломаные линии критического и подкритических путей постоянно находятся выше прямой линии, т.е. предполагаемая длительность выполнения работ больше планируе-
мой ( > ), принимаемые решения не эффективны и не способствуют сокращению общего срока окончанию работ.
Если ломаная линия критического пути и прямая линии совпадают, т.е. в каждый данный момент времени = , ход работ точно согласован с планом на протяжении выполнения всего комплекса работ.
Рис. 6.1. Динамика хода работ по сетевому графику
Если ломаная линия критического пути находится ниже прямой линии, т.е. в каждый данный момент времени < , прогнозируемая длительность выполнения работ опережает номинальную длительность по плану и принимаемые решения достаточно эффективны.
Следовательно, чем ниже ломаная линия (критического и подкритических путей) расположена относительно прямой, тем эффективнее принимаемые управленческие решения.
Чтобы оценить эффективность управления объектом и качество работы руководителей по сетевому графику, разработана целая система коэффициентов, которая учитывает относительное положение этих двух линий (критического и установленного планового срока свершения завершающего события) в каждый данный момент времени.
Если коэффициент эффективности управления в момент времени Т обозначить К„ планируемое время выполнения работ в Т-й момент 
, величину критического пути в момент Т 
, то можно предположить, что
В простейшем случае
(6.1)
Коэффициент эффективности управления по сетевому графику К можно определить по следующей формуле:
(6.2)
где Л — число периодов снятия информации по сетевому графику. Подставив в это уравнение формулу (6.1), получим
(6.3)
Определим области существования функции 
Если 0< < 
Неопределенность области существования такого коэффициента затрудняет его применение на практике. Для практического применения необходима такая система коэффициентов, которая была бы определена однозначно. Чтобы удобнее было применять коэффициент на практике, примем верхнюю границу его существования за единицу и потребуем, чтобы 1 > >0 при изменении аргумента
от 0 до
Таким образом, на функцию , накладываются следующие ограничения:
1.
Поскольку значение = 1 при значении аргумента 
= 0 является максимальным, то первая производная функции должна быть равна нулю, т.е. 
.=0 при 
=0
2. График функции с таким пределом должен иметь точку перегиба при значении аргумента, равным единице, т.е. в тот момент, когда = ( =1)справедливо:
В точке перегиба вторая производная равна нулю, а значит, справедливо следующее:
Функции, удовлетворяющие таким требованиям, могут быть представлены в следующем виде:
(6.4)
где А — условное значение коэффициента (будет определено ниже).
Чтобы удовлетворять условию 1, число п в любом случае должно быть больше единицы, т.е. > n >1.
При этом представляют интерес только те значения показателя п, при которых в момент времени, когда предполагаемая длительность выполнения работ совпадает с запланированной (в точке перегиба при = ), коэффициент эффективности управления не меньше 0,5, т.е. при равенстве планируемого и фактического сроков 
0.5
Исследуем влияние показателя п, принимающего значения 1,5; 2; 3; 4 на значение функции Выбор таких значений основывается на практическом применении коэффициентов эффективности управления.
Например, при значении n =1,5 функция (6.4) приобретает следующий вид:
(6.5)
Значение коэффициента А определяется из условия равенства нулю второй производной в точке перегиба, когда = :
тогда
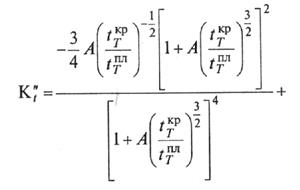
Вынося общие множители за скобки и сокращая их, получаем следующее выражение:
При 
=1 
= -1-А+6А=0, откуда А= 
Если найденное значение А подставить в формулу (6.5), то искомая функция примет вид
(6.6)
Произведя аналогичные вычисления, можно найти значения коэффициентов для различных значений А= 
;n=2:
(6.7)
при А= 
;n=3:
(6.8)
при А= 
;n=4:
(6.9)
Графическое изображение функций , представлено на рис. 6.2. Из него видно, что в момент времени, когда = (т.е. в точке перегиба) при n =1,5; 2; 3; 4 коэффициент принимает соответственно значения 0,83; 0,75; 0,66;,0,62. Такой диапазон Изменения коэффициента эффективности управления на практике наиболее приемлем, так как соответствует тому моменту, когда предполагаемая длительность выполнения работ совпадает с планируемой продолжительностью и резерв свершения событий критического пути равен нулю. Целесообразно остановиться на той системе, коэффициент эффективности управления которой равен 0,75. Она соответствует значению К,, определенному по формуле (6.7).
Рис. 6.2. Графическое изображение функции ,
Коэффициент эффективности управления за весь срок проведения работ по сетевому графику, исходя из формул (6.2) и (6.7), определяется следующим образом:
(6.10)
Управление объектом по системе СПУ может считаться эффективным при
0,5 < 
<1. Насколько близким к единице будет величина коэффициента К га, покажет практика применения этого метода. Руководителю всегда следует стремиться принимать настолько эффективные решения, чтобы значение коэффициента эффективности управления было как можно ближе к единице.
Вернемся к нашему примеру. На рис. 6.1 можно проследить динамику роста коэффициентов эффективности управления по сетевому графику, внедренному при выполнении капитального ремонта технологического оборудования. При построении графика вся зона разбивается на области, в точках пересечения их границ с периодами снятия информации определяются значения коэффициента ,. Как видно из рисунка, эффективность управления, характеризуемая величиной коэффициента повышается по мере сокращения продолжительности критического пути (при достижении = 0, =1) и понижается по мере его
увеличения и при превышении планового срока (при =0, =0). Когда планируемое время завершения работ совпадает с продолжительностью критического пути, т.е. ход работ точно согласуется с намеченным по плану (точки на наклонной прямой), коэффициент эффективности управления равен 0,75.
В каждый момент времени коэффициент эффективности управления определяется по формуле (6.7). Например, 15 мая по плану до окончания ремонтных работ согласно графику оставалось 15 дней, а продолжительность критического пути в это время составляла 18 дней, тогда
Аналогично были определены коэффициенты эффективности управления и по всем остальным периодам снятия информации. Общее число таких периодов равно 13. Динамика изменения показывает, что через два дня величина коэффициента эффективности управления составила 0,707, спустя шесть дней, когда величина достигла значения , — 0,750, а на 27 мая К' =1.
Далее по формуле (6.10) был определен усредненный коэффициент эффективности управления по системе СПУ:
=(0,676+0,680-0,707+0,720+0,740+0,745+0,750+0,775+0,804+0,844+ +0,894+0,956+1,00)/13 = 0,792.
Полученные значения коэффициентов показывают высокую эффективность управления комплексом работ (общий срок выполнения ремонтных работ был сокращен на 3 дня).
Метод количественной оценки эффективности управления объектом по сетевому графику с помощью предлагаемой системы коэффициентов позволяет объективно оценивать уровень руководства, т.е. эффективность принимаемых решений, оперативность, квалификацию и целенаправленность действий руководства.
Таким образом, система СПУ не только позволяет отыскивать оптимальные решения, ведущие к конечной цели самым коротким путем, но и помогает объективно оценивать работу руководителей и ответственных исполнителей и оперативно намечать действенные меры по повышению квалификации исполнителей и наиболее целесообразному распределению имеющихся ресурсов.