Эмпирических зависимостей

В начале этой лекции была сформулирована задача сглаживания опытных данных. Ее постановка имеет следующий вид.

При выполнении серии экспериментов получена следующая таблица значений исследуемой величины y при изменении величины x

Требуется по полученным данным найти аналитическое выражение приближенной зависимости между величинами y и x, значения которой при 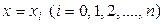мало отличаются от опытных данных .

Пусть, исходя из физических представлений о характере поведения искомой зависимости или характера расположения экспериментальных точек, определен общий вид эмпирической зависимости

,

в которой постоянные параметры неизвестны и подлежат определению. Как показано выше, значения параметров находят, используя опытные данные , .

Является очевидным, что если бы значения x и y измерялись в ходе эксперимента точно, то достаточно иметь только пар значений . Это число опытных точек позволяет составить систему из уравнений с искомыми параметрами . Такая система, если имеет решение, то оно будет единственным и являться решением поставленной задачи сглаживания опытных данных.

Фактически, экспериментальные данные всегда имеют случайные погрешности и, следовательно, любой набор из 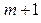пар данных не позволяет получить истинные значения параметров . Обычно с целью повышения точности оценки величины случайных погрешностей выполняют большее число опытов , что вызывает увеличение до количества уравнений

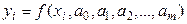, . (5)

В этом случае система (5) будет избыточной, несовместной, т. е. решение каких-либо уравнений из системы (5) могут не удовлетворять остальным уравнениям этой системы. В связи с этим под целью поставленной выше задачи понимается поиск наиболее вероятных значений параметров , которые будут удовлетворять всем уравнениям (5) наилучшим образом (хотя и неточно). Эти вероятные значения параметров будут тем ближе к истинным, чем больше число опытов.

Выше были рассмотрены два метода определения неизвестных параметров эмпирической формулы , основу которых составляет тот или иной способ минимизации отклонений ε _i значений выбранной функции от опытных данных y_i

, .

Обоим методам присущ общий недостаток. Каждый из них допускает многозначность решения. Так, полученное решение методом выбранных точек во многом зависит от того, как проведена кривая, аппроксимирующая опытные точки, какой ее вид и соответствующая ей функция были определены, а также от выбора на кривой точек для определения параметров .

В методе средних значения неизвестных параметров, в частности, зависят числа опытных точек и разбиения их на требуемое число групп.

Вместе с тем, в теории вероятностей применительно к получению при измерениях с одинаковой точностью наиболее достоверного результата установлено следующее положение. Если отклонения полученных результатов наблюдений распределены по нормальному закону, то наивероятнейшим результатом является такое значение, для которого сумма квадратов разностей этого значения и результатов наблюдений является наименьшей. Это положение получило название принципа наименьших квадратов.

Применим этот принцип для поиска неизвестных параметров 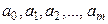эмпирической зависимости . В соответствие с принципом будем полагать, что наивероятнейшими значениями искомых параметров будут такие, при которых сумма квадратов отклонений ε _i значений выбранной функции от опытных данных y_i будет наименьшей, т. е.

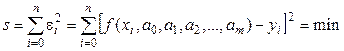, (i = 0, 1, 2,…, n). (6)

При этом считаем, что отклонения ε _i подчиняются нормальному закону распределения.

Поскольку в функции s (6) параметры являются независимыми переменными, то минимум функции s найдем, приравнивая нулю частные производные по этим переменным:

, , …, , (7)

Полученные в результате дифференцирования выражения (6) представляют собой систему уравнений для нахождения параметров .

Рассмотрим применение метода наименьших квадратов для частного случая, когда в качестве эмпирической функции используется многочлен степени m

. (8)

Такой случай задания эмпирической функции широко используется в практических задачах.

Подставив многочлен (8) в условие (6), получим

.

Выполнив дифференцирование функции s по искомым параметрам, находим

Приравнивая выражения для производных нулю в соответствии с требованием минимума функции s и раскрывая скобки, получим следующую систему уравнений:

Решив эту систему линейных алгебраических уравнений относительно параметров 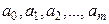многочлена (8), найдем значения этих параметров и, следовательно, решение задачи сглаживания опытных данных.

В заключение отметим, что все рассмотренные методы задачи сглаживания опытных данных применимы для определения неизвестных параметров в случае выбора нелинейных эмпирических зависимостей, в частности, степенной, экспоненциальной и др.

Линеаризация нелинейных эмпирических зависимостей. Если в качестве эмпирической формулы 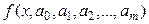выбрана нелинейная зависимость, то для нахождения ее параметров проводят преобразование нелинейной зависимости к линейной. Это производится путем преобразованием исходной системы координат и/или введением дополнительных переменных. Рассмотрим пример линеаризации нелинейной функции.

Пример. На рисунке 4 приведены результаты экспериментальных исследований зависимости между величинами y и x в виде точечного графика. По расположению точек опытных данных в качестве эмпирической формулы выбрана степенная функция вида

, (9)

в которой - неизвестные параметры. Такой случай расположения опытных данных часто встречается при изучении различных явлений, имеющих место при механической обработке металлов резанием.

Для нахождения параметров производится логарифмирование зависимости (9)

(10)

и переход к новой системе координат ln y, ln x, в которой строят точечный график, логарифмируя экспериментальные данные (рисунок 5). На полученном графике проводят прямую линию, которая наиболее близко примыкает к точкам экспериментальных данных.

По графику прямой уравнения (10) определяют величину отсекаемого отрезка ln a ₀ на оси ln y и величину коэффициента a ₁ по формуле

,

в которой 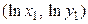, - координаты двух точек, выбранных на графике эмпирической прямой.

В рассматриваем примере: . Таким образом, эмпирическая формула зависимости между величинами y и x для экспериментальных данных примера имеет вид:

.

Примечание. Примеры линеаризации нелинейных зависимостей можно найти в [3].

Контрольные вопросы и упражнения для приобретения