однофакторного ортогонализиро-

Индивидуальное задание № 4

Однофакторный эксперимент

Однофакторное уравнение регрессии второго порядка, решение в программе MS Excel

Цель: освоить методы моделирования и оптимизации однофакторных тех- нических систем, описываемых стохастическими закономерностями.

Формулировка задачи. Зерно, собранное комбайном, имеет влажность

» 30 %. На току оно подсыхает до влажности » 20 %. Для долгосрочного хра- нения на элеваторе зерно должно иметь влажность 14 %. Для сушки зерна до указанной влажности используют специальные сушила, теплоносителем в ко- торых является горячий воздух. Важнейшим параметром, характеризующим эффективность работы сушила, является удельный расход энергии (пара- метр Y, кВт×ч/т). При прочих равных условиях удельный расход энергии зави- сит от температуры теплоносителя (фактор х 1, °С). Необходимо изучить зави- симость удельного расхода энергии Y от температуры теплоносителя х 1, варь-

ируемого в интервале x Î[ x, x ] = [60, 120] оС и определить оптимальный

1 1min 1max

режим функционирования сушила.

Математическая формулировка задачи: 1) построить адекватное уравне- ние регрессии, отражающее зависимость удельного расхода энергии (Y, кВтч/т) от температуры воздуха (х 1, ° С); 2) рассчитать оптимальное значе- ние фактора х 1опт (° С), при котором удельный расход энергии Y будет мини- мальным.

Решение задачи начнем с построения однофакторного уравнения регрессии

второго порядка на базе РСП с числом опытов

N = 5

и числом дублей

n = 4.

Результаты эксперимента приведены в таблице 1.

Таблица 1. – Экспериментальные данные для РСП

 

N	х 1 j, °С	Yj1, кВтч/т	Yj2, кВтч/т	Yj3, кВтч/т	Yj4, кВтч/т
		73,5	75,3	73,5	74,1
		60,4	60,2	63,7	61,5
		55,4	59,0	58,8	54,8
		54,8	55,5	54,3	51,9
		59,7	62,5	57,9	57,8

План решения задачи

1. Внимательно прочитать условия задачи.

2. Ввести исходные данные в таблицу MS Excel.

3. Создать МП для построения однофакторного ортогонализированного уравнения регрессии второго порядка и выполнить предварительную обра- ботку экспериментальных данных.

4. Создать ММ для построения однофакторного ортогонализированного уравнения регрессии второго порядка и выполнить окончательную обработку экспериментальных данных.

5. В случае адекватности однофакторного ортогонализированного урав- нения регрессии второго порядка провести оптимизацию изучаемого объекта:

рассчитать оптимальные значения факторов

X 1 опт

и x 1 опт, значение

Y min, а

также абсолютную ошибку

D Y min.

6. По результатам моделирования и оптимизации изучаемой технической си- стемы сделать вывод.

 

Решение задачи по плану

1. Пункт 1 выполнить самостоятельно.

2. Введём исходные данные в таблицу MS Excel:

3. Создадим МП для построения однофакторного уравнения регрессии вто-

рого порядка, которая состоит из столбцов: N,

X 1 j,

x 1 j, Y 1 j, Y 2 j, Y 3 j, Y 4 j

(из таб-

 

j

лицы 1), Yj, S:

 

Введём в МП значения границ интервалов варьирования в натуральных и нормированных координатах:

Для расчёта промежуточных значений фактора в остальных точках плана

можно использовать формулы (6) и (7)

x = x

+ j -1 × (x

- x),

j =1,..., N. (1)

1j 1min

N -1

1max 1min

X 1j

=-1 +2 × (j -1),

N -1

j =1,..., N. (2)

или команду MS Excel из ленты команд «Главная», «Прогрессия»:

 

Заполнив столбец фиктивного фактора

X 0 значениями 1, получим:

 

3.2 Проведем предварительную обработку экспериментальных данных:

3.2.1 выборочное среднее в каждом опыте Y j

ции MS Excel:

рассчитаем с помощью функ-

 

å Yji

Y = i = 1

, j =1,..., N; (3)

j n

3.2.2

j

выборочная дисперсия в каждом опыте S2:

å (Y - Y)

n

2

ji j

S 2 = i = 1,

 

j =1,..., N. (4)

j (n- 1)

рассчитывается с помощью функции MS Excel ДИСП.В( Выборочные значе- ния ):

Скопировав формулы для расчёта среднего значения и дисперсии в остальные строки таблицы, получим:

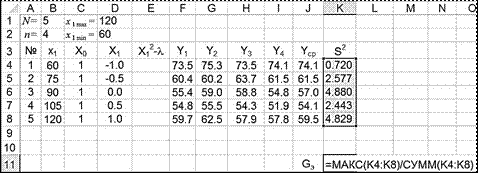
3.2.3. однородность выборочных дисперсий по критерию Кохрена:

- экспериментальное значение критерия Кохрена G _э (см. уравнение Ошибка! Источник ссылки не найден.):

j

max S 2

Gэ = N

j

å S 2

; (5)

j=1

- критическое значение критерия Кохрена

 

G

числ знам

;

f; f; p

при числах степеней

свободы

f числ = n -1 = 4 -1 = 3,

f знам = N = 5

при доверительной вероятности

р = 0,95 выбирается из таблицы приложения 5

Gf числ; f знам; p = Gn -1; N; p = G 3; 5; 0,95 =0,598.

Критическое значение критерия Кохрена можно рассчитать в программе MS Excel с помощью вспомогательной функции бета распределения:

БЕТА.ОБР( Вероятность, Альфа, Бета ),

в которой на место параметров следует подставить следующие значения:

Вероятность = 1 – (1 – p)/ N, Альфа = (n –1)/2, Бета = (N – 1)(n –1)/2.

В рассматриваемом примере расчёт критического значения критерия Кох- рена будет выглядеть следующим образом:

Вывод: выборочные дисперсии однородны, так как

G э = 0,316 < 0,598 = G 3;5; 0,95.

G э < Gn -1; N; p:

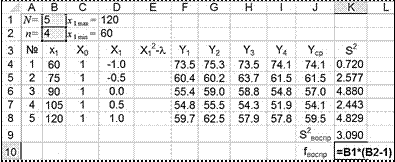
3.2.4.

воспр

Дисперсия воспроизводимости S ² находится, как среднее дисперсий

всех опытов:

å S

N

j

S

=

2

воспр

j = 1

 

N

а её число степеней свободы

f воспр = N (n -1):

 

;

4. Создадим ММ для построения однофакторного ортогонализированного

уравнения регрессии второго порядка на базе РСП с числом опытов

N = 5:

4.1. ММ для построения однофакторного ортогонализированного уравне-

ния регрессии второго порядка

Y = b X + b X + b (X 2 - l)

содержит

0 0 1 1 11 1 1

столбцы

N, X

, X,(X 2

 

- l), Y,

 

X Y, X Y, (X 2

 

- l) Y,

Y p, (Y

- Y p)2:

0 j j

1 j j

0 j j

1 j j

1 j 1 j

j j j

Ортогонализирующий коэффициент l:

N

å X 2

l 1 =

1 j

j = 1

N

= N + 1 3(N -1)

для РСП

(X

1 j

Рассчитаем значения ортогонализированного фактора

2 - l):

 

Обратите внимание, что ссылка на ячейку F1, содержащую l, задана в абсо- лютных координатах $F$1, чтобы при последующем копировании формулы в другие строки адрес ссылки не изменялся:

 

4.2. Рассчитаем коэффициенты

b 0, b 1, b 11

однофакторного ортогонализиро-

1 1

ванного уравнения регрессии второго порядка зультаты расчета внести в таблицу 4).

Y = b 0 X 0 + b 1 X 1+ b 11(X ² - 0,5)

(ре-

Рассчитаем произведения

 

X 0 j Y_j,

X 1 j Y_j, (X ² - l). Для этого в первой ячейке

введём формулу с абсолютной адресацией к столбцу $J, содержащему сомно- житель Y_ср:

После копирования формулы в остальные ячейки получим все необходимые произведения:

Рассчитаем их суммы:

Рассчитаем суммы квадратов столбцов факторов 5

X 2; 5

X 2;

(X ² - 0,5)²,

 

воспользовавшись функцией MS Excel СУММКВ():

å 0 j

j = 1

å 1 j

j = 1

å 1

j = 1

 

 

4.4. Рассчитаем коэффициенты однофакторного ортогонализированного

уравнения регрессии второго порядка b 0, b 1, b 11:

1 j

;

N N N

å X 0 j Y j

å X 1 j Yj

å(X ²

- l1) Yj

=

b

j = 1

å X

0 N

0 j

j = 1

j = 1

=

å X

b

1 N

1 j

j = 1

b 11

j = 1

=

N

1 j

å(X ²

j = 1

 

- l1)²

 

 

;

Скопировав формулу в соседние ячейки, получим:

 

 

 

4.5. Проверим коэффициенты

 

 

b 0, b 1, b 11

.

однофакторного ортогонализиро-

ванного уравнения регрессии второго порядка на значимость по критерию Стьюдента:

- рассчитаем дисперсии значимости коэффициентов регрессии

S ² (b 0), S ² (b 1), S ² (b 11):

 

1 j

S ² (b 0) =

S

воспр;

 

S ² (b 1) =

S

воспр

 

S ² (b 11) =

2

S

(X

воспр

 

n å

N

X

2

0 j

j = 1

N

X

n å

2

1 j

j = 1

N

n å

j = 1

2 -l)2

Обратите внимание на абсолютную адресацию ячеек, которая позволяет нам скопировать формулу для остальных коэффициентов:

 

- доверительные интервалы коэффициентов

b 0, b 1, b 11

Однофакторного орто-

гонализированного уравнения регрессии второго порядка

D b 0, D b 1, D b 11:

D b 0= t f; p × S (b 0);

D b 1= t f; p × S (b 1)

D b 11 = t f; p × S (b 11)

Критическое значение критерия Стьюдента t f; p при числе степеней свободы

fвоспр

и доверительной вероятности

p = 0,95

выбирается из таблицы приложе-

ния 2 или вычисляем с помощью встроенной функции MS Excel:

СТЬЮДЕНТ.ОБР.2Х( Вероятность; Степени свободы )

**

- регрессионные коэффициента

b 0, b 1, b 11 значимы, так как:

D b 0 = 0,838 < 61,23 = b 0;

D b 1= 1,185 < 7,315 = b 1

D b 11 = 2,002 <10,74 = b 11

Вывод: однофакторное ортогонализированное уравнение регрессии вто- рого порядка, в котором все коэффициенты значимы, имеет вид

Y = 61,23 - 7,315× X 1 +10,74 × (X ² - 0,5).

4.6.

Проверим однофакторное ортогонализированное уравнение регрес-

сии второго порядка терию Фишера:

Y = 61,23 - 7,315× X 1 +10,74 × (X ² - 0,5)

на адекватность по кри-

Y

j

- Расчетные значение p в каждом опыте вычислим, как сумму произведе-

ний коэффициентов регрессии на значения соответствующих факторов. Обра- тите внимание на абсолютные адреса ссылок на коэффициенты регрессии:

 

 

-

j

Рассчитаем квадраты отклонений (Yj - Y ^p)²:

 

-

j

Остаточная сумма квадратов j рассчитывается по уравнению:

(

N

j = å Y

j = 1

j - Y ^p)2

 

- Рассчитаем дисперсию адекватности

2 и её число степеней свободы

f ад:

S

S

ад

=

2 n j;

ад N - B

f ад = N - B

;

- Экспериментальное значение критерия Фишера F _э:

max(S ², S ²)

F э =

воспр ад

 

min(S ², S ²)

воспр ад

 

-

числ знам

Критическое значение критерия Фишера Ff; f; p, в котором на первом

месте стоит число степени свободы

f числ= f ад = N - B = 5 - 3 = 2

большей диспер-

сии, а на втором - число степени свободы

f числ = f воспр = N (n -1) = 5× (4 -1) =15

Мень-

шей дисперсии, при доверительной вероятности

p = 0,95

выбирается из таб-

лицы приложения 4 или рассчитывается с помощью встроенной функции MS Excel:

F.ОБР( Вероятность, Степени свободы числителя, Степени свободы знаме- нателя )

числ знам ад воспр

Ff; f; p = Ff; f; p = FN - B; N (n -1); p = F 2; 15; 0,95 =3, 682.

Вывод: однофакторное ортогонализированное уравнение регрессии

второго порядка

Y = 61,23 - 7,315× X 1 +10,74 × (X ² - 0,5)

адекватно по критерию Фи-

шера, так как Fэ = 1,630 < F 2;15; 0,95 = 3,682

 

5. Оптимизация изучаемой технической системы.

5.1. Параметр Y (X 1) имеет минимум, так как b 11 =10.7 > 0:

- Рассчитаем оптимальное значение фактора натах:

X 1 опт

в нормированных коорди-

X 1опт

=- b 1

2 b 11

 

 

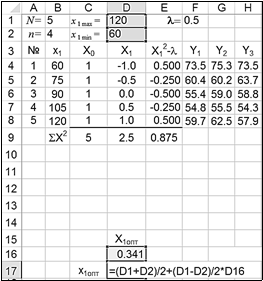
- Оптимальное значение фактора

x 1 опт

в натуральных координатах:

X = x 1 - x 10;

 

 

x = x + X D x

1 D x 1

1 10 1 1

x = x 1max + x 1min; D x = x 1max - x 1min

10 2 1 2

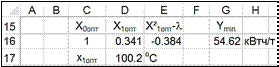
- Для расчёта минимального значение параметра Y _min в уравнение регрессии

необходимо рассчитать сумму произведений

b 0, b 1, b 11 на

X 0, X 1опт, (X 2

-l):

1 опт

 

5.2. Абсолютная погрешность

D Y min

параметра

Y min, значение которого рас-

считывается по однофакторному ортогонализированному уравнению ре- грессии второго порядка Y = 61, 24 - 7,312 × X 1 + 10, 74 × (X ² - 0,5), определим:

D Y (X 1) = tN (n -1), p ×

 

С учетом полученных значений

D b 0,

D b 1,

D b 11

и D Y min

корректно округлим ре-

зультатов расчета

D b 0,

D b 1,

D b 11

и D Y min:

 

 

6.

Окончательный вывод. Однофакторное ортогонализированное уравне- ние регрессии второго порядка со значимыми регрессионными коэффициен-

тами

Y = 61, 2 - 7,3 X 1+ 10, 7 × (X ² - 0,50)

адекватно описывает процесс сушки зерна.

Минимальные энергозатраты при сушке зерна при температуре воздуха

x 1 опт =100 ^oC составляют Y min = (54,6 ±1, 2) кВт× ч/ т.

Ответ: Ортогонализированное однофакторное уравнение регрессии второго порядка

Y = 61, 2 - 7,3 × X 1 + 10, 7 × (X ² - 0,50), кВт× ч/т.

±0,8 ±1,2 ±2,0

S

Дисперсии всех опытов однородны, т.к. Gэ = 0,316 < 0,598 = G 3; 5; 0,95.

S

2

воспр

= 3, 090;

f воспр =15;

2 = 5, 024;

f ад = 2.

ад

Уравнение регрессии второго порядка адекватно, так как

F э = 1,630 < 3,682 = F 2;15; 0,95;

Оптимальные параметры: Y min= (54,6 ±1, 2) кВтч/ т;

X 1 опт = 0,341;

x 1 опт » 100 oC.

Вывод: Однофакторное ортогонализированное уравнение регрессии второго порядка со статистически значимыми регрессионными коэффициентами

Y = 61, 2 - 7,3 X 1 + 10, 7 × (X ² - 0,50) адекватно описывает процесс сушки зерна. Мини-

мальные энергозатраты при сушке зерна будут достигнуты при температуре

воздуха

x 1 опт = 100 oC

и составят Y min = (54,6 ±1, 2) кВт× ч/ т.