Понятие о сложной электрической цепи. Методы расчета сложных электрических цепей: -законы Кирхгофа; -метод контурных токов; -метод узловых потенциалов; -метод наложения.
К сложным электрическим цепям относят цепи, содержащие несколько источников электрической энергии, включенных в разные ветви. Ниже на рис. изображены примеры таких цепей.
Для сложных электрических цепей неприменима методика расчета простых электрических цепей. Упрощение схем невозможно, т.к. нельзя выделить на схеме участок цепи с последовательным или параллельным соединением однотипных элементов. Иногда, преобразование схемы с ее последующим расчетом все-таки возможно, но это скорее исключение из общего правила.
Для полного расчета сложных электрических цепей обычно используют следующее методы:
1.Применение законов Кирхгофа (универсальный метод, сложные расчеты системы линейных уравнений).
Порядок расчета цепей, связанный с использованием законов Кирхгофа следующий:
1) Выбирают положительные направления токов в ветвях электрической цепи.
2) Составляют (k-1) независимых уравнений по первому закону Кирхгофа. Уравнения составленные по первому закону Кирхгофа гораздо проще уравнений, составленных по второму закону Кирхгофа. Поэтому их составляют максимально возможное количество.
3) Выбирают (l-k+1-m) независимых контуров электрической цепи. Контуры необходимо выбирать так, чтобы в них вошли все ветви схемы. Контуры взаимно независимы, если каждый последующий выбираемый контур содержит не менее одной новой ветви.
4) Для каждого из выбранных независимых контуров выбирают направления обхода и составляют уравнение по второму закону Кирхгофа.
5) 
Решают систему из (l-m) линейных уравнений любым удобным способом.
2.Метод контурных токов (универсальный метод)
Расчет сложных электрических цепей методом контурных токов производят в следующей последовательности:
1) Вычерчиваем принципиальную схему и все ее элементы.
2) На схеме выбирают и обозначают контурные токи, таким образом, чтобы по любой ветви проходил хотя бы один выбранный контурный ток (исключая ветви с идеальними источниками тока). Контуры можно выбирать произвольно, лишь бы их число было равно (l-k+1-m), и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие.
3) Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов используют сдвоенные арабские цифры (или римские).
4) Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов ветвей можно использовать одиночные арабские цифры.
5) По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. Уравнения составлят в следующем виде:
6) Решаем любым методом полученную систему относительно контурных токов и определяем их.
7) Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви. При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.
3.Метод узловых напряжений (универсальный метод)
Метод узловы́х потенциалов — метод расчета электрических цепей путём записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях.
Узловыми напряжениями называют напряжения между каждым из (k-1) узлов и одним произвольно выбранным опорным узлом. Потенциал опорного узла принимается равным нулю. На схеме такой узел обычно отображают как заземленный.
Сущность метода заключается в том, что вначале решением системы уравнений определяют потенциалы всех узлов схемы по отношению к опорному узлу. Далее находят токи всех ветвей схемы с помощью закона Ома.
Расчет сложных электрических цепей методом узловых напряжений производят в следующей последовательности:
1) Вычерчиваем принципиальную схему и все ее элементы.
2) На схеме произвольно выбирают и обозначают опорный узел. В качестве опорного желательно выбирать узел, в котором сходится максимальное количество ветвей.
3) Произвольно задаемся направлением токов всех ветвей и обозначаем их на схеме.
4) Для определения потенциалов остальных (k-1) узлов по отношению к опорному узлу составляем следующую систему уравнений:
5) Решаем любым методом полученную систему относительно узловых напряжений и определяем их.
6) Далее для каждой ветви в отдельности применяем закон Ома и находим все токи в электрической цепи.
4.Принцип наложения (универальный метод, несложные расчеты).
Метод наложения — метод расчёта электрических цепей, основанный на предположении, что ток в каждой из ветвей сложной электрической цепи при всех включённых источниках электрической энергии, равен алгебраической сумме токов в этой же ветви, полученных при включении каждого из генераторов по очереди и отключении остальных генераторов.
Ток в любой ветви можно рассчитать как алгебраическую сумму токов, вызываемых в ней каждым источником электрической энергии в отдельности. При этом следует иметь ввиду, что когда ведут расчет токов, вызванных одним из источников электрической энергии, то остальные источники ЭДС в схеме замещают короткозамкнутыми участками, а источники тока разомкнутыми участками.
Данный метод позволяет существенно упростить расчеты сложных электрических цепей, содержащих небольшое количество источников электрической энергии.
Расчет сложных электрических цепей методом наложения производят в следующей последовательности:
1) Вычерчиваем принципиальную схему и все ее элементы.
2) Произвольно задаемся направлением токов всех ветвей и обозначаем их.
3) Определяем количество источников электрической энергии на схеме.
4) Для каждого источника электрической энергии вычерчиваем отдельную дополнительную схему, на которой выбранный источник отображаем без изменений (по сравнению с исходной схемой),а остальные источники замещаем (источники ЭДС на короткозамкнутый участок, источник тока на разомкнутый участок электрической цепи).
5) Для каждой из вновь вычерченной схемы обозначаем токи ветвей таким образом, чтобы не путать их с реальными токами ветвей исходной схемы (например если на исходной схеме ток ветви обозначен как I1, то на дополнительных схемах обозначаем его I1', I1'', I1''' и т.д.).
6) Рассчитываем каждую дополнительную схему в отдельности по методике расчета простых электрических цепей.
7) Определяем токи ветвей исходной схемы путем алгебраического суммирования токов ветвей всех дополнительных схем. Если направление тока на дополнительной схеме совпадает с направлением, указанным на основной схеме, ему присваивают знак "+", в противном случае присваивают знак "-".
5.Метод эквивалентного источника (удобен когда необходимо произвести не полный расчет электрической цепи, а найти ток в одной из ветвей).
Метод эквивалентного источника позволяет произвести частичный анализ электрической цепи. Например, определить ток в какой-либо одной ветви электрической цепи или исследовать поведение этой ветви при изменении ее сопротивления. Применение данного метода может оказаться полезным как при частичном расчете сложных электрических цепей, так и простых.
Метод эквивалентного источника применяют в следующей последовательности:
1) Вычерчиваем принципиальную схему и все ее элементы.
2) Заданную условием задачи схему разбивают на две части: ветвь (или участок электрической цепи) в которой требуется найти значение тока и остальную часть схемы.
3) Производят замену активного двухполюсника на эквивалентный источник напряжения или тока.
4) Находят значение тока в заданной ветви, применив одно из следующих соотношений: 
6.Метод эквивалентного преобразования схемы (применим довольно редко, простые расчеты).
Метод эквивалентного преобразования схемы используют при расчете простых электрических цепей. В отдельных случаях имеется возможность применить его и для расчета сложных электрических цепей.
Суть метода эквивалентного преобразования схемы заключается в упрощении схемы, когда два (или несколько) однотипных элемента электрической цепи замещаются одним эквивалентным элементом того же типа. Под термином "эквивалентный элемент" подразумевается такой элемент, замещение на который не меняет значений токов и напряжений в остальной части электрической цепи.
| Метод контурных токов |
Метод контурных токов используется для расчета резистивных линейных цепей с постоянными токами и для расчета комплексных схем замещения линейных цепей с гармоническими токами. При этом в расчет вводятся контурные токи – это фиктивные токи, которые замыкаются в независимых замкнутых контурах, отличающихся друг от друга наличием хотя бы одной новой ветви.
Методика расчета цепи методом контурных токов
В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.
Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:
1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы.
2 Определяем все независимые контуры.
3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.
4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.
5 Решаем любым методом полученную систему относительно контурных токов и определяем их.
6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).
7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.
При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.
Пример расчёта сложной цепи методом контурных токов
В цепи, изображённой на рисунке 1, рассчитать все токи методом контурных токов. Параметры цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.
Рис. 1. Схема электрической цепи для примера расчета по методу контурных токов
Решение. Для расчета сложной цепи этим методом достаточно составить два уравнения, по числу независимых контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. рисунок 1).
По второму закону Кирхгофа относительно контурных токов составляем уравнения:
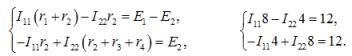Решаем систему и получаем контурные токи I11 = I22 = 3 А.
Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. На рисунке 1 такими токами являются I1, I2, I3. Направление у этих токов одинаковое – вертикально вверх.
Переходим от контурных токов к реальным. В первой ветви протекает только один контурный ток I11. Направление его совпадает с направлением реального тока ветви. В таком случае реальный ток I1 + I11 = 3 А.
Реальный ток второй ветви формируется двумя контурными I11 и I22. Ток I22 совпадает по направлению с реальным, а I11 направлен навстречу реальному. В результате I2 = I22 - I11 = 3 - 3 = 0А.
В третьей ветви протекает только контурный ток I22. Направление этого тока противоположно направлению реального, поэтому для I3 можно записать I3 = -I22 = -3А.
Следует отметить, как положительный факт, что в методе контурных токов по сравнению с решением по законам Кихгофа приходитсярешать систему уравнений меньшего порядка. Однако этот метод не позволяет сразу определять реальные токи ветвей.
|
Метод узловых потенциалов
Метод узловых потенциалов – один из методов анализа электрической цепи, который целесообразно использовать, когда количество узлов в цепи меньше или равно числу независимых контуров. Данный метод основан на составлении уравнений по первому закону Кирхгофа. При этом, потенциал одного из узлов цепи принимается равным нулю, что позволяет сократить число уравнений до n-1.
Рассмотрим пример
1 – Для начала примем узел 4 за базовый и будем считать его потенциал равным нулю.
2 - Составим уравнения по первому закону Кирхгофа для узла 1,2,3 (для узла 4 не составляем, так как это не требуется)
3 – Используя обобщённый закон Ома составим уравнения для нахождения каждого из токов (за ϕi берем потенциал узла из которого ток выходит, а за ϕ потенциал узла в который ток входит) Gi – проводимость i-ой ветви.
4 – Подставим полученные выражения для токов в уравнения из пункта 2, получим
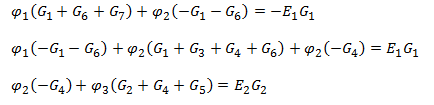
Данная система уравнений записана для цепи состоящей из 4 узлов, а для n узлов справедливо
Проводимости G11,G22 и т.д. – сумма проводимостей сходящихся в узле (собственные проводимости), всегда берутся со знаком плюс. Проводимости G12,G21 и т.д. проводимости ветвей соединяющих узлы (общие проводимости), всегда берутся со знаком минус.
Если источник тока или ЭДС направлен к узлу, то берем со знаком плюс, в противном случае со знаком минус.
5 – Решив систему уравнений из пункта 4 любым доступным способом, найдем неизвестные потенциалы в узлах, а затем определим с помощью них токи.
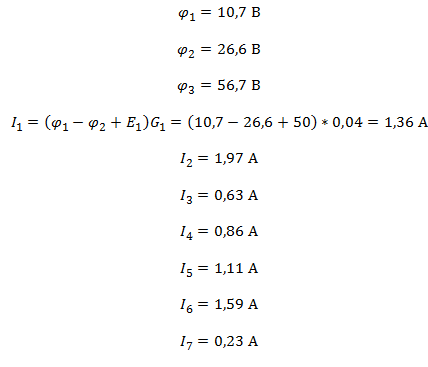
Правильность решения проверим с помощью баланса мощностей
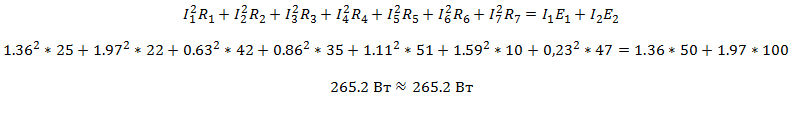
Задача решена верно методом узловых потенциалов.