Центрально-растянутые и центрально-сжатые элементы

Раздел 1. Деревянные конструкции

Задание. Исходные данные

Табл. 1

№ вари анта	№ рис. (схемы)	Тип сече ния	Размеры в мм	Схема закреп ления концов в плоскости	Най ти
ℓ	b	h	d	a	c	х - х	у - у
		а	-						-	-	N
		а						-	Ш-З	Ш-З	N
		б		d/3	-		-	-	Ш-Ш	З-З	N
		а				-		-	-	-	Ϭ; τ; f
		а		-	-	-	-	-	-	-	b; h
		а				-	-	-	-	-	Ϭ; τ; f
		а		-	-	-	-	-	-	-	b; h
		а				-	-	-	-	-	Ϭ; τ; f
		б	-						-	-	N
		б						-	З-О	З-Ш	N
		а				-	-		Ш-З	Ш-З	N
		а		-	-	-		-	-	-	b; h
		а				-	-	-	-	-	Ϭ; τ; f
		а		-	-	-	-	-	-	-	b; h
		а				-	-	-	-	-	Ϭ; τ; f
		а		-	-	-	-	-	-		b; h
		а	-						-	-	N
		а						-	З-З	З-О	N
		б		d/3	-		-	-	Ш-З	О-З	N
		а				-		-	-	-	Ϭ; τ; f
		а		-	-	-	-	-	-	-	b; h
		а				-	-	-	-	-	Ϭ; τ; f
		а		-	-	-	-	-	-	-	b; h
		а							-	-	Ϭ; τ; f
		б	-						-	-	N
		б						-	З-Ш	Ш-Ш	N
		а				-	-		З-О	З-Ш	N
		а		-	-	-		-	-	-	b; h
		а							-	-	Ϭ; τ; f
		а		-	-	-	-	-	-	-	b; h

Примечание: 1. Буквы в графе «Схема закрепления концов в плоскости» означают: Ш - шарнирное; 3 - защемление; О - свободное (без раскреплений).

2. Тип сечения: а – прямоугольное; б – круглое.

ва ри ант	Номер задачи аналога	Усло вия эксплуа тации	Материал	Сорт древе сины	Загружение	примечание
N кН	q кН/м
		А1	лиственница		-	-	элемент связи
		Б2	сосна		-	-	элемент стойки
		БЗ	ель			-	элемент стойки
		В1	береза		-		балка межэт.пер
		В2	пихта			-	консоль
		А2	дуб		-		консоль
		Б1	ясень			-	балка черд.перек
		А1	кедр		-		балка межэт.пер
		Б2	вяз		-	-	элемент связи
		Б3	клен		-	-	элемент стойки
		А1	лиственница			-	элемент стойки
		Б2	сосна		-		прогон
		БЗ	ель			-	консоль
		В1	береза		-		консоль
		В2	пихта			-	балка черд.перек
		А2	дуб		-		балка межэт.пер
		Б1	ясень		-	-	элемент связи
		А1	кедр		-	-	элемент стойки
		Б2	вяз		-	-	элемент стойки
		Б3	клен		-		балка черд.перек
		А1	лиственница			-	консоль
		Б2	сосна		-		консоль
		БЗ	ель			-	балка черд.перек
		В1	береза		-		балка межэт.пер
		В2	пихта		-	-	элемент связи
		А2	дуб		-	-	элемент стойки
		Б1	ясень		-	-	элемент стойки
		А1	кедр		-		балка межэт.пер
		Б2	вяз			--	консоль
		Б3	клен		-		консоль

Табл. 2

 

Примечание

1.Нагрузки заданы расчетные.

РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ

ИЗ ДЕРЕВА ПО СНиП П-25-80 [1]

ЦЕНТРАЛЬНО-РАСТЯНУТЫЕ И ЦЕНТРАЛЬНО-СЖАТЫЕ ЭЛЕМЕНТЫ

Центральное растяжение и сжатие

Основные расчетные формулы для проверки цент­рально-растянутых и сжатых элементов [1, п. 4.1.,4.2.]:

напрочность N/ А_нт≤R _р; N/ А_нт≤R _c;

на устойчивость сжатых элементов N/ А_расч≤φR _c;

где

R_{р, с} - расчетное сопротивление древесины (сосны, ели), принимается по [1, табл. 3].

Расчетные сопротивления, приведенные в табл. 3, следует умножать на коэффициенты условий работы согласно [1,п. 3.2]:

а) для различных условий эксплуатации конструкций – на значения коэффициент m _в, указанные в табл. 5;……..

и) для растянутых элементов с ослаблением в расчетном сечении и изгибаемых элементов из круглых лесоматериалов с подрезкой в расчетном сечении – на коэффициент m _о = 0,8.

А_нт - площадь нетто ослабленного сечения. Ослабления для растянутого элемента считаются совмещенными в одном сечении, если расстояние между ними меньше 200 мм;

А_расч - расчетная площадь сжатого элемента, принимается равной А_бр - без ослаблений или при площади ослаблений А_осл < 25% А _бр;

(4/3)А_нт - при площади ослаблений > 25% А _бр;

А_нт - при симметричных ослаблениях, выходящих на грань сечения;

φ - коэффициент продольного изгиба находится по гибкости элемента λ [1, п. 4.3.].

Для древесины коэффициент φ подсчитывается по формулам:

при λ ≤ 70 φ ═ 1-0,8(λ/100) ²

при λ ≥ 70 φ ═ 3000/ λ²

Для других материалов значения коэффициентов φ можно подсчитать по формулам [1].

Гибкость элемента определяется по формуле [1, п. 4.4.]:

λ ═ ℓ₀ /r ═ μ_оℓ/√J/А

где ℓ₀ _ расчетная длина элемента [1, п. 4.5.; п. 4.21. п. 6.25.];

r - радиус инерции сечения;

μ₀ - коэффициент приведенной длины (для деревянных конструкций) принимается равным:

1 - для шарнирно опертого стержня;

2,2 - для стержня с одним защемленным и другим свободным концами;

0,8 - для стержня с одним защемленным и другим шарнирно опертым концами;

0,65-для защемленного с двух концов стержня.

Для прямоугольного сечения размером bh радиусы инерции можно подсчитывать по формулам:

r_х = 0,289h, r_у = 0,289в.

Для круглого сечения диаметром dрадиусы инерции r_х = r_у = d/4.

Гибкость элементов не должна превышать предельных величин, установленных [1, табл.14].

Примеры решения

Задача 1. Найти несущую способность растянутого элемента. Исходные данные: h = 200мм;b = 150мм; а=120мм; с=300мм; d=16мм; материал - лиственница; сорт древесины 1; условия эксплуатации А1.

 

Рис. 1

Решение. Несущую способность элемента при заданных условиях задачи вычисляем по формуле

N = т₀ т_п т_в R _р A_нт

где т ₀ - коэффициент, учитывающий наличие ослаблений, равен 0,8;

т _п- коэффициент перехода на породу дерева, для лиственницы равен 1,2 [1, табл. 4];

т _в- коэффициент, учитывающий условия эксплуатации (группу конструкций), равен 1,0 [1, табл.5];

R_р - расчетное сопротивление древесины (сосны, ели), принимается по [1, табл. 3 п. 2. а] и равно 10 МПа.

Для вычисления A_нтвыбираем самый опасный участок, где на расстоянии 200 мм имеет место наибольшая площадь ослаблений (не попадающих при перемещении вдоль волокон одно на другое). Такой участок будет на участке с отверстиями 1, 2 и 3.

А_нт= bh - 3db = 20•15 - 3•1,6•15 = 228 см².

Несущая способность растянутого элемента

N = 0,8•1,2•1,0•10•0,0228 = 0,21888 мН = 218,88 кН.

Задача 2. Найти несущую способность центрально-сжатого стержня

Исходные данные: h = 200мм;b = 150мм; а=150мм; ℓ =3000мм; d=55 мм; материал - пихта; сорт древесины 2; условия эксплуатации А3; условия закрепленияконцов стержня в плоскостях х-х и у – у: шарнирное (Ш-Ш).

 

Рис. 2.

 

Решение. Несущая способность центрально-сжатого стержня с учетом его устойчивости подсчитывается по формуле

N =φ т_п т_в R_с A_расч

где т_п = 0,8 [1, т.4]; т_в = 0,9 [1, т.5];

R_с = 13 МПа (для сосны второго сорта) Поскольку сечение ослаблено отверстием d = 55 мм, площадь ослабления равна

А_осл= dh = 5,5•20 = 82,5 см², что составляет 100 %•82,5 / 20•15 = 27,5 % > 25 %.

Расчетная площадь сечения при проверке устойчивости

А_расч = (4/З) А_нт = (4/3)(300-82,5) = 290 см².

Для определения коэффициента φ подсчитаем гибкость элемента:

λ_х = μ_оℓ/0,289 b = 1,0•300/0,289•15 = 69,2

λ_у = μ_оℓ/0,289 h = 1,0•300/0,289•20 = 51,9

Расчет ведем на большую гибкость λ_х = 69,2

Для гибкости λ<70 определяем коэффициент φ

φ ═ 1-0,8(λ/100)² ═ 1-0,8(69,2/100) ²=0,617

Несущая способность стержня

N = 0,617•0,0290•0,8•0,9•13= 0,1692 мН = 169,2кН.

 

Задача 3. Проверить несущую способность центрально-сжатого стержня. Исходные данные: N = 100Кн; h = 225мм;b = 150мм; с=20мм; ℓ =4000мм; материал - сосна; сорт древесины 2; условия эксплуатации А1, условия закрепленияконцов стержня в плоскости х-х: защемление и шарнирное опирание (З-Ш) и в плоскости у – у: шарнирное опирание (Ш-Ш).

 

Рис. 3.

Решение. Проверка несущей способности центрально-сжатого стержня производится по формуле

N =φ т_п т_в R_с A_расч

Для рассматриваемого варианта т_п = 1,0;

т_в = 1,0;

R_с = 13 мПа.

Сечение имеет симметричное ослабление, выходящее на кромку сечения. Для такого стержня

A_расч = А_нт=(15•22,5) - 2•2•15 = 277,5 см²

Гибкость стержня

λ_х = μ_оℓ/0,289 h = 0,8•400/0,289•22,5 = 49,2

λ_у = μ_оℓ/0,289 b = 1,0•400/0,289•15 = 92,3

 

Наибольшая гибкость λ_у = 92,3 > 70, для нее коэффициент продольного изгиба

φ ═ 3000/ λ² ═ 3000/92,3²=0,352

Проверка несущей способности стержня:

N = 100 кН < φ т_п т_в R_с A_расч = 0,352•0,02775•1,0•1,0•13000 = 126,98 кН.

Вывод: несущая способность стержня достаточна.

 

ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ

Основные расчетные проверочные формулы поперечно изогнутых элементов следующие:

Ϭ ═ М/W_нт ≤ R_и;

τ ═ QS/Jb≤ R_ск или 1,5Q/bh - для прямоугольного сечения;

М/W_бр ≤ φ_м R_и; где φ_м ═ 140 k_ф b /h ℓ_р;

f/ℓ ≤ |f/ℓ|

В написанных формулах приняты следующие обозначения:

М - изгибающий момент в проверяемом сечении;

Q - поперечная сила;

J - момент инерции поперечного сечения;

W_нт - момент сопротивления нетто проверяемого сечения;

S- статический момент сдвигаемой части сечения относи­тельно нейтральной оси;

b, h - размеры поперечного сечения;

k_ф - коэффициент, учитывающий форму эпюры изгибающих моментов на участке ℓ_р, принимается по [1, при л. 4, табл.2];

R_и, R_ск - расчетное сопротивление древесины (сосны, ели), принимается по [1, табл. 3 п. 2. а];

Прогиб балки не должен превышает предельной величины, установленной [1, табл.16].

 

Задача 4. Проверить прочность и прогибы балки прогона цельного прямоугольного сечения. Исходные данные: q^н = 10Кн/м; h = 225мм;b = 150мм; а=1000мм; ℓ =4000мм; материал - сосна; сорт древесины 2; условия эксплуатации А1. Рис 4.

Решение. Предварительно находятся величины:

М_пр = q/2(ℓ²/4-а²) = 10/2(4²-1²) = 15кНм;

М_оп = q а²/2 = 10•1²/2 = 5кНм;

Q_пр = qℓ/2= 10•4/2 = 20кН;

Q_оп = qа= 10•1 = 10кН;

Внимание! Здесь приведены формулы определения внутренних усилий на опоре и в пролете: М_пр; М_оп; Q_пр; Q_оп только для расчетной схемы, представленной на рис.4. Для расчетных схем рис.5, 6, 7 и 8.необходимо предварительно построить эпюры М и Q, определить их наибольшие значения.

W_{нт =} bh²/6 = 15•22.5²/6 = 1265,625 см² (ослаблений нет);

S₌ bh²/8 =15•22,5²/8 = 949,22 см²;

J ₌ bh³/12 =15•22,5³/12 = 14238,281 см².

R_и = 14 МПа; R_ск =1,6 МПа.

Проверка прочности:

Ϭ ═ М/W_нт =15•10³/1265,625 = 11,85 МПа < R_и = 14 МПа;

τ ═ QS/Jb =20•10•949,22 /14238,281•15 = 0,89 МПа < R_ск = 1,6 МПа.

Прочность обеспечена.

Полный прогиб

f_о= qа(ℓ³ – 6а²ℓ-3а³)/24ЕJγ_f = 10•1•10 (4³- 6•1²•4 - 3•1³)/24•10⁵•14238,28•1,2 = 0,902 см;

где

Е = 10⁴МПа = 10⁵кгс/см² [1,п. 3.5. – модуль упругости древесины вдоль волокон].

γ_f=1,2 – усредненный коэффициент перехода к расчетам по 2-му предельному состоянию.

f_пр = qℓ²(5/8ℓ² -3а³)/48ЕJγ_f = 10•4² •10⁵(5/8 •4² - 3•1³)/48•10⁵•14238,28•1,2

=1,366 см;

Проверка прогибов: f/ℓ = 1,366/400 = 1/293 < [1/200]

Прогиб балки не превышает предельного [1, табл.16].

Задача 5. Из условия прочности подобрать размеры попе­речного сечения балки. Исходные данные: q^н = 13 кН/м; а=1100мм; ℓ =4500мм; материал - ясень; сорт древесины 2; условия эксплуатации В1. Рис 4.

Сечения принимать согласно сортаменту пиломатериалов.

 

Решение. Предварительно находятся величины:

М_пр = q/2(ℓ²/4-а²) = 13/2(4,5²-1,1²) = 25,04 кНм;

М_оп = q а²/2 = 13•1,1²/2 = 7,865 кНм;

Q_пр = qℓ/2= 13•4,5/2 = кН;

Q_оп = qа= 13•1,1 =14,3кН;

Находится требуемый момент сопротивления:

W_тр═ М/ R_и т_в = 25,04•10⁴/13•1,3•10 = 1481,66 см^3;

где R_и = 13МПа [1, табл. 3 п. 1. а];

т_п = 1,3 для ясеня [1, табл. 4 п. 6].

Задаемся шириной сечения b = 15 см. Тогда требуемая высота сечения

h_тр = √ 6W/ b = √ 6•1481,66/15 = 24,34 см ≈ 25 см.

Принимаем сечение = 15 х 25 см (см. табл.3 приложения 1).

Момент сопротивления принятого сечения

W = bh²/6 = 15•25²/6 = 1562,5 см³.

Проверка прочности:

Ϭ ═ М/W=25,04•10³/1562,5 = 16,03 МПа < R_и т_п = 13•1,3 = 16,9 МПа;

τ ═ QS/Jb = 1,5Q/bh (для прямоугольного сечения),

где Q - максимальная поперечная сила,

τ = 1.5•29,25•10/15•25 = 1,17 МПа < R_ск т_п = 1,6•1,3 = 2,56 МПа;

где R_ск = 1,6МПа [1, табл. 3 п. 5. а];

т_п = 1,3 для ясеня [1, табл. 4 п. 6].

Прочность обеспечена.

 

Приложение 1

Сортамент пиломатериалов (ГОСТ 8486 - 86*Е) табл. 3

Толщина, мм	Ширина, мм
					-	-	-	-	-
						-	-	-	-
								-	-
					17.5	.200
	-
	-	-							-
	-	-	-						-
	-	-	-	-					-
	-	-	-	-	-				-
	-	-	-	-	-	-	-		-

Приложение 2

Формулы для определения максимальных прогибов:

f= Nℓ³/3ЕJ – консольная балка

f= qℓ⁴/8ЕJ - консольная балка

f= Рℓ³/48ЕJ –балка на двух опорах

f= 5qℓ⁴/384ЕJ - балка на двух опорах

Приложение 3

Рис. 4 Рис. 5

Рис. 6 Рис. 7

Рис. 8

 

Приложение 4.

Выдержки из СНиП П-25-80 «Деревянные конструкции» [1]

 

 

3. Расчетные характеристики материалов

3.1. Расчетные сопротивления древесины сосны (кроме веймутовой), ели, лиственницы европейской и японской приведены в табл. 3.

Таблица 3

Напряженное состояние и характеристика элементов	Обозначение	Расчетные сопротивления, , для сортов древесины
1. Изгиб, сжатие и смятие вдоль волокон:
а) элементы прямоугольного сечения (за исключением указанных в подпунктах “б”, “в”) высотой до 50 см	R и, R с, R см	14	13	8,5
б) элементы прямоугольного сечения шириной свыше 11 до 13 см при высоте сечения свыше 11 до 50 см	R и, R с, R см	15 150	14 140	10 100
в) элементы прямоугольного сечения шириной свыше 13 см при высоте сечения свыше 13 до 50 см	R и, R с, R см	16 160	15 150	11 110
г) элементы из круглых лесоматериалов без врезок в расчетном сечении	R и, R с, R см	_	16 160	10 100
2. Растяжение вдоль волокон:
а) неклееные элементы	R р	10 100	7 70	_
б) клееные элементы	R р	12 120	9 90	_
3. Сжатие и смятие по всей площади поперек волокон	R с90, R см90	1,8 18	1,8 18	1,8 18
4. Смятие поперек волокон местное:
а) в опорных частях конструкций, лобовых врубках и узловых примыканиях элементов	R см90	3 30	3 30	3 30
б) под шайбами при углах смятия от 90 до 60°	R см90	4 40	4 40	4 40
5. Скалывание вдоль волокон:
а) при изгибе неклееных элементов	R ск	1,8 18	1,6 16	1,6 16
б) при изгибе клееных элементов	R ск	1,6 16	1,5 15	1,5 15
в) в лобовых врубках для максимального напряжения	R ск	2,4 24	2,1 21	2,1 21
г) местное в клеевых соединениях для максимального напряжения	R ск	2,1 21	2,1 21	2,1 21
6. Скалывание поперек волокон:
а) в соединениях неклееных элементов	R ск90	1 10	0,8 8	0,6 6
б) в соединениях клееных элементов	R ск90	0,7 7	0,7 7	0,6 6
7. Растяжение поперек волокон элементов из клееной древесины	R р90	0,35 3,5	0,3 3	0,25 2,5

Расчетные сопротивления для других пород древесины устанавливаются путем умножения величин, приведенных в табл. 3, на переходные коэффициенты m _п, указанные в табл. 4.

Таблица 4

	Коэффициент m п для расчетных сопротивлений
Древесные породы	растяжению, изгибу, сжатию и смя	сжатию и смятию поперек волокон R с90, R см90	ска­лыванию R ск
тию вдоль волокон R р, R и, R с, R см
Хвойные
1. Лиственница, кроме европейской и японской	1,2	1,2
2. Кедр сибирский, кроме Красноярского края	0,9	0,9	0,9
3. Кедр Красноярского края, сосна веймутова	0,65	0,65	0,65
4. Пихта	0,8	0,8	0,8
Твердые лиственные
5. Дуб	1,3		1,3
6. Ясень, клен, граб	1,3		1,6
7. Акация	1,5	2,2	1,8
8. Береза, бук	1,1	1,6	1,3
9. Вяз, ильм		1,6
Мягкие лиственные
10. Ольха, липа, осина, тополь	0,8		0,8

Примечание. Коэффициенты m _п, указанные в таблице для конструкций опор воздушных линий электропередачи, изготавливаемых из не пропитанной антисептиками лиственницы (при влажности £ 25%), умножаются на коэффициент 0,85.

3.2. Расчетные сопротивления, приведенные в табл. 3, следует умножать на коэффициенты условий работы:

а) для различных условий эксплуатации конструкций – на значения коэффициент m _в, указанные в табл. 5; Таблица 5

Условия эксплуатации (по табл. 1)	Коэффициент m в	Условия эксплуатации (по табл. 1)	Коэффициент m в
А1, А2, Б1, Б2		В2, В3, Г1	0,85
А3, Б3, В1	0,9	Г2, Г3	0,75

……………………………………………………………………………………………………..…

и) для растянутых элементов с ослаблением в расчетном сечении и изгибаемых элементов из круглых лесоматериалов с подрезкой в расчетном сечении – на коэффициент m _о = 0,8;

………………………………………………………………………………………………………..

3.5. Модуль упругости древесины при расчете по предельным состояниям второй группы следует принимать равным: вдоль волокон Е = 10 000 МПа (100 000 кгс/см²); поперек волокон Е ₉₀ = 400 МПа (4000 кгс/см²). Модуль сдвига древесины относительно осей, направленных вдоль и поперек волокон, следует принимать равным G ₉₀ = 500 МПа (5000 кгс/см²). Коэффициент Пуассона древесины поперек волокон при напряжениях, направленных вдоль волокон, следует принимать равным n_90.0 = 0,5, а вдоль волокон при напряжениях, направленных поперек волокон, n_0.90 = 0,02.

………………………………………………………………………………..

4. Расчет элементов деревянных конструкций

А. Расчет элементов деревянных конструкций по предельным состояниям первой группы.

Центрально-растянутые и центрально-сжатые элементы

4.1. Расчет центрально-растянутых элементов следует производить по формуле

, (4)

где N – расчетная продольная сила;

R _p – расчетное сопротивление древесины растяжению вдоль волокон;

F _нт – площадь поперечного сечения элемента нетто.

При определении F _нт ослабления, расположенные на участке длиной до 200 мм, следует принимать совмещенными в одном сечении.

4.2. Расчет центрально-сжатых элементов постоянного цельного сечения следует производить по формулам:

а) на прочность

; (5)

б) на устойчивость

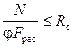, (6)

где R _с – расчетное сопротивление древесины сжатию вдоль волокон;

j – коэффициент продольного изгиба, определяемый согласно п. 4.3;

F _нт – площадь нетто поперечного сечения элемента;

F _рас – расчетная площадь поперечного сечения элемента, принимаемая равной:

при отсутствии ослаблений или ослаблениях в опасных сечениях, не выходящих на кромки (рис. 1, а), если площадь ослаблений не превышает 25% Е _бр, Е _расч = F _бр, где F _бр – площадь сечения брутто; при ослаблениях, не выходящих на кромки, если площадь ослабления превышает 25% F _бр, F _рас = 4/3 F _нт; при симметричных ослаблениях, выходящих на кромки (рис. 1, б), F _рас = F _нт.

 

 

4.3. Коэффициент продольного изгиба j следует определять по формулам (7) и (8);

при гибкости элемента l £ 70

; (7)

при гибкости элемента l > 70

, (8)

где коэффициент а = 0,8 для древесины и а = 1 для фанеры;

коэффициент А = 3000 для древесины и А = 2500 для фанеры.

4.4. Гибкость элементов цельного сечения определяют по формуле

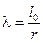, (9)

где l _о – расчетная длина элемента;

r – радиус инерции сечения элемента с максимальными размерами брутто соответственно относительно осей Х и У.

4.5. Расчетную длину элемента l _о следует определять умножением его свободной длины l на коэффициент m₀

l _о = l m₀ (10)

согласно пп. 4.21 и 6.25 ………………..

ми.

Изгибаемые элементы

4.9. Расчет изгибаемых элементов, обеспеченных от потери устойчивости плоской формы деформирования (см. пп. 4.14 и 4.15), на прочность по нормальным напряжениям следует производить по формуле

, (17)

где М – расчетный изгибающий момент;

R _и – расчетное сопротивление изгибу;

W _рас – расчетный момент сопротивления поперечного сечения элемента. Для цельных элементов W _рас = W _нт;…………………………………………………………………………………