Основные характеристики смо

Содержание

Введение. 3

Системы массового обслуживания 4

Понятия о СМО 5

Основные характеристики смо 7

Классификация смо 8

Смо с потерями. 9

Смо с ожиданием. 10

Содержания 14

 

 

ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ

Введение

Теория массового обслуживания является важным разделом системного анализа и исследования операций. Она богата разнообразными приложениями: от задач. связанных с эксплуатацией телефонных сетей, до научной организации производства. Эта теория используется там, где имеются вызовы и клиенты, сигналы и изделия массового производства, а также там, где изделия обслуживаются, обрабатываются, передаются.

Идеи и методы теории массового обслуживания (ТМО) получают всё большее распространение. Многие задачи техники, экономики, военного дела, естествознания могут быть поставлены и решены в терминах ТМО.

Своим возникновением ТМО обязана, в первую очередь, прикладным вопросам телефонии, в которых из-за большого числа независимых или слабо зависимых источников (абонентов телефонных станций) потоки заявок (вызовов) имеют четко выраженный случайный характер. Случайные колебания (флуктуации) около некоторого среднего являются в данном случае не результатом какого-то отклонения от нормы, а закономерностью, свойственной всему процессу. С другой стороны, стабильность работы телефонных станций, возможность получения хороших статистических данных создали предпосылки для выявления основных характеристик, свойственных данному процессу обслуживания.

Впервые на это обратил внимание и провёл исследования датчанин А.К. Эрланг. Основные его работы в данной области относятся к 1908 - 1921 годам. С этого времени, интерес к проблемам, выдвинутым Эрлангом, необычайно возрос. В 1927 - 1928 годах появляются работы Молина и Фрайя, позже в 1930 - 1932 годах - интересные работы Поллачека, А.Н. Колмогорова, А.Я. Хинчина.

Нужно сказать, что первые задачи ТМО были достаточно простыми и допускали получение окончательных аналитических зависимостей. О, развитие шло как по линии увеличения сферы приложения ТМО, так и по линии усложнения стоящих перед ней задач. Оказалось, что задачи типа телефонных, возникают в самых разнообразных направлениях исследований: в естествознании. в технике, на транспорте, в военном деле, в организации производства и т.д.

 

 

Системы массового обслуживания

Во многих областях практической деятельности человека мы сталкиваемся с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях в билетных кассах, в крупных аэропор­тах, при ожидании обслуживающим персоналом самолетов разрешения на взлет или посадку, на телефонных станциях в ожидании освобождения линии абонента, в ремонтных цехах в ожидании ремонта станков и обо­рудования, на складах снабженческо-сбытовых организаций в ожидании разгрузки или погрузки транспортных средств. Во всех перечисленных случаях имеем дело с массовостью и обслуживанием. Изучением таких ситуаций занимается теория массового обслуживания.

Теория массового обслуживания – область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные события повторяются многократно, например, на предприятиях бытового обслуживания; в системах приема, переработки и передачи информации; автоматических линиях производства и др.

Предметом теории массового обслуживания является установление зависимостей между характером потока заявок, числом каналов обслуживания, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами.

 

Понятие смо

В теории систем массового обслуживания (СМО) обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе.

Средства, обслуживающие требования, называются обслуживающими устройствами или каналами обслуживания. Например, к ним относятся каналы телефонной связи, посадочные полосы, мастера-ремонтники, би­летные кассиры, погрузочно-разгрузочные точки на базах и складах.

Совокупность однотипных обслуживающих устройств называется системой массового обслуживания. Такими системами могут быть телефонные стан­ции, аэродромы, билетные кассы, ремонтные мастерские, склады и базы снабженческо-сбытовых организаций и т.д.

Основной задачей теории СМО является изучение режима функциони­рования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслужи­вающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время без­действия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории СМО возникают задачи оптимизации: каким образом достичь оп­ределенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с просто­ем обслуживающих устройств.

Источник. Источник определяется как устройство или множество, из которого требования поступают в систему для обслуживания. Источник называют бесконечным или конечным в зависимости от того, бесконечное или конечное число требований содержится в нем. Будем всегда предполагать, что источник, генерирующий требования, неисчерпаем. Например, хотя абонентов некоторого телефонного узла конечное число, предполагаем, что они образують бесконечный источник.

Входящий поток. Требования, поступающие из источника на обслуживание, образуют входящий поток. Само требование можно рассматривать как запрос на удовлетворение какой-то потребности. Примеров входящих потоков можно привести множество. Это — поток информации, поступающей на обработку в ЭВМ; поток заявок на АТС; поток клиентов, приходящих в ателье, и больных в поликлинику, поток прибывающих в порт судов; налетающие на объект удара самолеты и ракеты противника и т. д.

Обслуживающая система. Под обслуживающей системой понимают множество технических средств или производственного персонала (различного рода установки, приборы, устройства, тоннели, взлетно-посадочные полосы, линии связи, продавцы, бригады рабочих или служащих, кассиры и т. д.), выполняющих функции обслуживания. Все перечисленное выше, как уже говорилось, объединяется одним названием «канал обслуживания» (обслуживающий прибор). Состав системы определяется количеством каналов (приборов, линий). По количеству каналов системы можно подразделить на одноканальные и многоканальные.

Выходящий поток. Выходящий поток — это поток требований, покидающих систему после обслуживания. Сюда могут входить и требования, которые покинули систему, не пройдя обслуживания.

Входящий поток, функционирование обслуживающей системы как результат обслуживания, выходящий поток подлежат количественному описанию. Для того чтобы проводить математические исследование процесса массового обслуживания, необходимо полно определить систему обслуживания. Обычно это означает:

— задание входящего потока. Здесь имеются в виду как средняя интенсивность поступления требований, так и статистическая модель их поступления (т. е. закон распределения моментов поступления требований в систему);

— задание механизма обслуживания. Это означает указание того, когда обслуживание допустимо, сколько требований может обслуживаться одновременно и как долго длится обслуживание. Последнее свойство обычно характеризуют статистическим распределением длительности обслуживания (закон распределения времени обслуживания);

— задание дисциплины обслуживания. Это означает указание способа, по которому происходит отбор одного требования из очереди (если она есть) на обслуживание. В простейшем варианте дисциплина обслуживания заключается в обслуживании требований в порядке их поступления (справедливый принцип), однако существует и много других возможностей.

Задание системы предполагает также известное описание взаимодействия между отдельными ее частями.

Когда система достаточно полно определена, появляется основание для построения математической модели. Если математическая модель более или менее адекватно отображает реальную систему, то она позволяет получить основные характеристики функционирования системы. Разумеется, модель значительно упрощает практическую ситуацию, но это не умаляет математических методов теории массового обслуживания и положение дел не отличается от положения дел в других областях прикладной математики.

 

Рис.23.1. Структурная схема типичной системы массового обслуживания

Основные элементы смо

Основными элементами СМО являются:входящий поток требований, очередь требований, обслуживающие устройства, (каналы) и выходящий поток требований. Потоком называют последовательность событий. Поток, состоящий из требований на обслуживание, называют потоком требований. Поток требований, поступающих в обслуживающую систему, называют входящим потоком. Поток требований, которые обслужены, называют выходящим потоком. Совокупность очередей и приборов (каналов) обслуживания называются системой обслуживания.

Основные характеристики смо

Значение P₀определяет вероятность того, что все каналы обслуживания свободны (находятся в состоянии простоя). Значение P_k определяет вероятность того, что в системе (в очереди и на обслуживании) находятся k заявок. Если k не превышает числа каналов N, то все заявки находятся на обслуживании и очередь отсутствует; в противном случае все каналы заняты и k-N заявок находится в очереди.

Вероятность P_отк отказа в обслуживании определяется ситуацией занятости всех N каналов и всех m мест в очереди и равна P_N+m.

Среднее число занятых каналов N_зан определяется математическим ожиданием дискретной случайной величины

Среднее число свободных каналов

Коэффициент простоя каналов

Коэффициент занятости каналов

Относительная пропускная способность (доля обслуженных заявок в общем числе поступавших в систему) определяется величиной

Абсолютная пропускная способность (среднее число заявок, обслуживаемых в единицу времени) определяется величиной

Средняя длина очереди

Среднее число заявок, находящихся в системе, складывается из средних значений занятости каналов и длины очереди

Среднее время пребывания заявки в очереди равно

Общее время пребывания заявки в очереди будет складываться из Tочер и среднего времени обслуживания

Полученные характеристики дают возможность анализа замкнутых и разомкнутых систем с отказами (m=0), с очередью или с ожиданием (m →∞) при простейшем входном потоке и однотипных параллельных каналах обслуживания с показательным законом длительности обслуживания (в частности, с фиксированной длительностью).

Классификация смо

По времени пребывания требований в очереди до начала обслуживания системы делятся на три группы:

1) с неограниченным временем ожидания (с ожиданием ),

2) с отказами;

3) смешанного типа.

В СМО с неограниченным временем ожидания очередное требование, застав все устройства занятыми, становится в очередь и ожидает обслуживания до тех пор, пока одно из устройств не освободится.

В системах с отказами поступившее требование, застав все уст­ройства занятыми, покидает систему. Классическим примером системы с отказами может служить работа автоматической телефонной станции.

В системах смешанного типа поступившее требование, застав все устройства занятыми, становится в очередь и ожидает обслуживания в течение ограниченного времени. Не дождавшись обслуживания в установ­ленное время, требование покидает систему.

В системах с определеннойдисциплиной обслуживания поступившее требование, застав все устройства занятыми, в зависимости от своего приоритета, либо обслуживается вне очереди, либо становится в оче­редь.

Смо с потерями.

Итак, в систему, состоящую из m линий, поступает про­стейший поток вызовов с интенсивностью , при этом каждый принятый вызов обслуживается с интенсивно­стью . При поступлении очередного вызова могут быть две ситуации:

1. хотя бы одна линия свободна, тогда вызов принимается и обслуживается свободной лини­ей;

2. все линии заняты обслуживанием, тогда вызов получает отказ и покидает систему, то есть теряется (от­сюда и название система с потерями). Таким образом, при отсутствии свободной линии вызов покидает сис­тему (теряется), не оказывая на нее никакого влияния. На рис. 2 приведен граф состояний СМО с потеря­ми.

Рис. 23.2. Граф состояний СМО с потерями

Состояние системы , k = 0, 1, 2,…, m, определяет­ся числом занятых линий k, которое равно числу вызо­вов, обслуживаемых системой. Переход вправо (всегда с интенсивностью при простейшем потоке) означает поступление очередного вызова и увеличение числа за­нятых линий на одну. Переход влево означает заверше­ние обслуживания одной линии и ее освобождение. При этом интенсивность перехода зависит от состояния: переход w_k → w_k-1 происходит с интенсивностью , так как в состоянии обслуживается одновремен­но k вызовов. Это обстоятельство приводит к заверше­нию обслуживания одного из вызовов (с интенсивнос­тью ), при этом одна линия освобождается, то есть число занятых линий уменьшается на 1. Таким обра­зом, в данном случае занятие линии рассматривается как рождение вызова, а освобождение линии (заверше­ние обслуживания вызова) – как гибель вызова.

Рассмотрим сначала однолинейную систему (m = 1). Число состояний такой системы равно двум. Предель­ные вероятности состояний будут

,

где – удобный параметр, равный отношению соответствующих интенсивностей.

Вероятность потерь , или вероятность того, что произвольный вызов, поступивший в систему, будет потерян, то есть получит отказ в обслуживании ввиду отсутствия свободной линии, а также среднее число за­нятых линий находят по формулам

,

Перейдем теперь к многолинейной СМО с потеря­ми. Предельные вероятности состояний

, ,

Эти формулы для предельных вероятностей числа занятых линий носят название формул Эрланга. Вид­но, что предельные вероятности зависят от параметра и числа линий m. Предельная вероятность состояния имеет следующий смысл: – это средняя доля време­ни на интервале бесконечно большой длины, в течение которого занято ровно k линий.

Вероятность потерь и среднее число занятых линий:

,

Таким образом, потери и загруженность линий зависят от параметра р и числа линий m. Интересно отметить, что при возрастании потери растут, а при убывании () потери уменьшаются ().

Смо с ожиданием.

Имеется система с m линиями обслуживания. При по­ступлении очередного вызова в систему с ожиданием могут быть две ситуации в зависимости от состояния системы: 1) хотя бы одна линия свободна, вызов при­нимается и обслуживается свободной линией; 2) все линии заняты, вызов не покидает систему, он становит­ся в очередь и ожидает, пока не освободится какая-ли­бо линия, при освобождении линии она берет вызов из очереди.

Итак, при отсутствии свободной линии вызов по­ступает в очередь. После освобождения линии он об­служивается, а после обслуживания вызов освобождает линию и покидает систему. Таким образом, главная особенность системы с ожиданием состоит в том, что необслуженные вызовы образуют очередь и ждут осво­бождения линий. Очередь образуется из вызовов, ожи­дающих обслуживания в момент, когда все линии заня­ты. При освобождении линии вызов на обслуживание берется из очереди. Длина очереди является случайной и может быть как угодно велика. Отличие данной сис­темы от системы с потерями заключается в том, что по­терь в прежнем виде нет. Обслуживание вызова, по­ставленного в очередь, только задерживается.

Состояние системы удобно обозначать числом вы­зовов, находящихся в системе. На рис. 3 показан граф состояний системы для обслуживания простейшего потока. Множество состояний является счетным (чис­ло возможных состояний бесконечно, так как очередь может быть бесконечной).

Рис. 23.3. Граф состояний СМО с ожиданием

Интенсивности переходов w_k → w_k+1 определя­ются параметром простейшего потока и поэтому не зависят от состояния. Интенсивности переходов w_k → w_k-1 зависят от состояния:

1. при 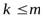очереди нет, все вызовы обслуживаются, поэтому ;

2. при или , , обслуживается m вызовов, а l вызовов () находятся в очереди, поэтому .

Характеристики СМО с ожиданием являются более разнообразными, чем характеристики СМО с потеря­ми. Ограничимся рассмотрением вероятностей состоя­ний, вероятности задержки обслуживания и среднего числа занятых линий.

Для случая однолинейной системы (m = 1) предель­ные вероятности состояний определяются по формуле

,

Вероятность задержки обслуживания и среднее число занятых линий соответственно будут

,

Перейдем к многолинейной СМО с ожиданием, то есть m>1. Состояния системы могут быть двух видов:

1. состояния, в которых очереди нет, ;

2. со­стояния, в которых очередь есть, .

Прежде всего предельная вероятность состояния вычисляется по формуле

Видно, что под знаком второй суммы находится геоме­трический ряд со знаменателем . Найдем сумму этого ряда при условии, что или :

С учетом этого формулы для предельных вероятностей примут вид

,

,

,

Вероятность задержки обслуживания и среднее число занятых линий:

,

Интересно отметить, что при условии или рассмотренный выше геометрический ряд сходится. В противном случае он расходится. Условие сходимос­ти ряда имеет следующий смысл. Число оп­ределяет наибольшую производительность системы. Если , то система справляется с обслуживанием, если же , то система не справляется с обслужи­ванием, при этом длина очереди неограниченно возра­стает, предельные вероятности не существуют.

Из проведенных рассуждений следует, что СМО с потерями может обслужить любой входящий поток, при этом чем больше интенсивность потока, тем боль­ше потери. А система с ожиданием может обслужить поток ограниченной мощности, для которого обяза­тельно должно выполняться условие , так как при очередь бесконечно растет. Система с ожидани­ем является более сложной по сравнению с системой с потерями, так как она требует создания бункера с нео­граниченной емкостью для создания очереди. Наличие такого бункера объясняет независимость среднего чис­ла занятых линий от количества линий в системе.

Пример:

Пусть СМО состоит из трех линий и обслуживает про­стейший поток с интенсивностью 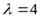1/ч. Интенсив­ность обслуживания 1/ч.

Рассмотрим оба типа СМО: СМО с потерями и СМО с ожиданием.

По условию число линий m = 3;

;

1. Для СМО с потерями получаем следующие ха­рактеристики:

;

;

;

2. Для СМО с ожиданием условие существования установившегося режима выполняется (), то есть система справляется с обслуживанием, поэтому предельные вероятности состояний существу­ют. Характеристики системы:

;

;

;

Сравнение полученных результатов показывает, что вероятность задержки вызова в СМО с ожиданием в два раза превышает вероятность потерь в другой сис­теме, но при этом линии используются более эффек­тивно: в среднем заняты две линии из трех, в то время как в СМО с потерями в среднем занято около полови­ны линий.

 

Список литературы

1. Ивченко Г.И., Каштанов В.А., Коваленко И.Н. Теория массового обслуживания. — Учебное пособие для вузов. — М.: Высшая школа, 1982. — 256 с. — 20 000 экз.

2. Клейнрок Л. Теория массового обслуживания. Пер. с англ. / Пер. И.И. Грушко; ред. В.И. Нейман. — М.: Машиностроение, 1979. — 432 с. — 10 000 экз.

3. Матвеев В.Ф., Ушаков В.Г. Системы массового обслуживания. — М.: МГУ, 1984. — 240 с.

4. Математический энциклопедический словарь / Гл. ред. Прохоров Ю.В.. — М.: Советская энциклопедия, 1988. — 847 с.