Работоспособность деталей, конструкций и узлов машин характеризуется рядом критериев: прочностью, износостойкостью, устойчивостью, жесткостью, теплостойкостью и др. Расчет надежности базируется на сопоставлении расчетного значения заданного критерия с его предельным значением, которое выбирают по нормативным и справочным материалам или устанавливают опытным путем (по результатам специальных испытаний или наблюдений при эксплуатации).
Работоспособность деталей, конструкций или узлов по заданному критерию считают обеспеченной, если расчетное значение критерия Y меньше его предельного значения Y пред. Это условие выполняют, используя коэффициент безопасности n, связывающий упомянутые значения параметров (n = Y пред / Y); соответственно расчетное условие можно выразить неравенством
 .
.
В вероятностных расчетах значения Y и Y пред рассматривают как случайные и независимые величины, распределенные по нормальному закону. В свою очередь их разность также считают случайной величиной, распределенной по тому же закону. Показателем надежности является вероятность безотказной работы Р по заданному критерию. Для обеспечения вероятности Р должно быть выполнено условие
 ,
,
где 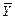 ,
, 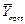 – средние значения величин Y и Y пред;
– средние значения величин Y и Y пред;
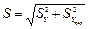 – среднее квадратическое отклонение разности двух случайных величин Y и Y пред;
– среднее квадратическое отклонение разности двух случайных величин Y и Y пред;
SY и SY пред – средние квадратические отклонения величин Y и Y пред;
up – квантиль нормированного нормального распределения.
Вероятность безотказной работы  по заданному критерию определяют по таблицам в зависимости от величины квантили:
по заданному критерию определяют по таблицам в зависимости от величины квантили:
 .
.
Связь между квантилью up и коэффициентом безопасности, рассчитанным по средним значениям  , имеет вид
, имеет вид
 ,
,
где 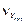 и
и 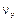 – коэффициенты вариации,
– коэффициенты вариации,
 ;
;
 .
.
Таким образом, зная квантиль или вероятность безотказной работы Р, можно оценить коэффициент безопасности  .
.
В общем случае параметр Y может зависеть от различных факторов и может быть выражен функциональной зависимостью
 ,
,
где xi – случайный фактор.
В свою очередь среднее значение 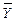 выражают зависимостью
выражают зависимостью
 .
.
Среднее квадратическое отклонение параметра Y определяют из выражения
 ,
,
где  – частная производная функции φ по фактору xi, в которую подставляют среднее значение фактора
– частная производная функции φ по фактору xi, в которую подставляют среднее значение фактора  ;
;
Si – среднее квадратическое отклонение i- го фактора.
На практике широко используются следующие методы оценки способности деталей и конструкций выдерживать нагрузки, основанные на расчетах:
1) по допускаемым напряжениям;
2) по запасам прочности;
3) прочностной надежности по вероятности разрушения или вероятности безотказной работы.
Расчеты на прочность по допускаемым напряжениям и запасам прочности позволяют на стадии проектирования дать приближенную оценку прочности деталей и конструкций, но они не учитывают случайного характера влияния нагружения.
Вероятностные расчеты прочности позволяют учесть фактор случайности и перейти от оценки прочности по коэффициентам прочности к оценке вероятности безотказной работы и прогнозированию ресурса деталей и конструкций.
Необходимо отметить, что использование вероятностных расчетов усложняет этап конструирования и проектирования машин. Поэтому предварительно необходимо определить номенклатуру деталей и конструкций, для которых подобные расчеты целесообразны. При этом нужно учитывать следующие соображения.
Во-первых, одним из факторов, определяющих необходимость использования вероятностных методов расчета прочности, является ограничение проектируемой детали или конструкции по размерам, т. е. отсутствие возможности обеспечения больших запасов прочности. Например, в механических трансмиссиях машин к ним можно отнести зубчатые передачи и подшипники качения. В таких случаях, когда необходимо обеспечить малые запасы прочности, целесообразно производить вероятностные расчеты.
Во-вторых, необходимо учитывать характер нагружения деталей и конструкций машины. При действии случайных нагрузок методы оценки их прочности по коэффициентам запаса прочности дают большую погрешность.
И, наконец, в-третьих, следует учитывать возможность изменения прочностных характеристик материалов при нагружении деталей и конструкций. Случайный характер их изменения также является основанием для вероятностных расчетов.
Таким образом каждый из перечисленных факторов (необходимость обеспечения малых запасов прочности, случайные характеры нагружения и изменения физико-механических характеристик материалов) обусловливает целесообразность проведения вероятностных расчетов.
В расчетах вероятности безотказной работы по критерию прочности обычно рассматривают три вида ресурсных отказов деталей и конструкций, происходящих из-за разрушений:
1) статических, происходящих в результате кратковременного (от одного до нескольких десятков циклов нагружения) приложения больших сил;
2) малоцикловых, которые являются основными для конструкций, работающих в течение 102–105 циклов нагружения;
3) усталостных (многоцикловых), возникающих в деталях при большом числе циклов нагружения (более 105);
В качестве расчетных параметров Y при оценке надежности по критерию прочности выбирают расчетные напряжения или нагрузку. Предельными параметрами Y пред считают пределы прочности, текучести, выносливости или несущую способность.
При расчетах прочности деталей и конструкций машин полагают, что распределения нагрузок F и прочности σ подчиняются нормальному закону распределения с плотностями вероятностей f (F) и f (σ) соответственно. Количественно эти параметры задают их числовыми характеристиками – средними значениями (математическими ожиданиями)  и
и  , средними квадратическими отклонениями SF и S σ или коэффициентами вариации vF и v σ. Если плотности распределения f (F) и f (σ) имеют участок взаимного пересечения (рисунок 5.11), то вероятность отказа будет определяться площадью этого участка.
, средними квадратическими отклонениями SF и S σ или коэффициентами вариации vF и v σ. Если плотности распределения f (F) и f (σ) имеют участок взаимного пересечения (рисунок 5.11), то вероятность отказа будет определяться площадью этого участка.
 Как видно из рисунка 5.11, с увеличением рассеяния нагрузок и механических свойств материала она будет возрастать.
Как видно из рисунка 5.11, с увеличением рассеяния нагрузок и механических свойств материала она будет возрастать.
Функцию надежности можно определить из выражения
 ,
,
где Ф (и) – нормированная нормальная функция распределения, которая, как уже отмечалось, табулирована, и ее значения можно определить по соответствующим таблицам нормального распределения.
В расчетах деталей машин прочность оценивают по соотношению расчетного σр и предельного σпред (по критерию прочности) напряжений, превышение которого вызывает отказ детали. Вероятность безотказной работы определяют как вероятность того, что расчетные напряжения не превышают предельных. Числовое значение этой вероятности определяют по таблицам нормального распределения в зависимости от квантили, если известны средние значения параметров  и
и  , средние квадратические отклонения S σр и S σпред или коэффициенты вариации
, средние квадратические отклонения S σр и S σпред или коэффициенты вариации  и
и 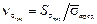 . В этом случае квантиль можно получить из выражения
. В этом случае квантиль можно получить из выражения
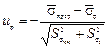 ,
,
которое можно выразить через запас прочности  :
:
 .
.
Изнашивание является сложным процессом, зависящим от многочисленных физико-химических, конструктивных, технологических и эксплуатационных факторов. Как отмечалось, наиболее характерным для дорожных, строительных и других машин является абразивное изнашивание, которое происходит в результате микрорезания или многократного деформирования материала детали под действием абразивных частиц. Этот вид изнашивания является преобладающим для элементов рабочего и ходового оборудования, а также узлов трения машин при попадании абразивных частиц в зону трения.
При оценке надежности по критерию износостойкости в инженерных расчетах ее наиболее информативной характеристикой является линейный износ: чем ниже износ, тем выше износостойкость детали. Оценку надежности можно вести по изменению (уменьшению) линейного размера одной детали при изнашивании, а также по изменению соотношения линейных размеров сопряженных деталей (увеличению зазора в подшипниках, шага зубчатых и цепных передач и др.). Текущую величину износа I можно оценить, используя выражение
 ,
,
где J – интенсивность изнашивания;
v – скорость относительного перемещения трущихся поверхностей;
t – время работы узла трения.
Предельно допустимая величина износа Δ связана с размерами детали (начальным значением L нач и предельно допустимым значением, при износе до которого наступает отказ, L пред) простым соотношением
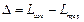 .
.
Если известны параметры L нач и L пред, а также другие характеристики изнашивания, вероятность безотказной работы детали Р можно определить по квантили нормального распределения
 ,
,
где 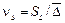 – коэффициент вариации размера детали;
– коэффициент вариации размера детали;
 – для предельно допустимого уменьшения размера;
– для предельно допустимого уменьшения размера;
 – для предельно допустимого увеличения размера (зазора);
– для предельно допустимого увеличения размера (зазора);
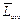 – среднее значение начального размера;
– среднее значение начального размера;
 – среднее квадратическое отклонение начального размера;
– среднее квадратическое отклонение начального размера;
 – условный коэффициент запаса по износу, (отношение средних значений предельно допустимого износа
– условный коэффициент запаса по износу, (отношение средних значений предельно допустимого износа  к действительному);
к действительному);
 – среднее значение интенсивности изнашивания;
– среднее значение интенсивности изнашивания;
 – коэффициент вариации интенсивности изнашивания.
– коэффициент вариации интенсивности изнашивания.
При оценке работоспособности узла трения важной задачей является правильный выбор предельно допустимых величин износа деталей узла, поскольку нормативы на эти величины имеются для ограниченной номенклатуры деталей. Она не имеет общих рекомендаций, поскольку предельное состояние определяют для конкретного типа сопряжений, узлов и машин с учетом последствий отказов. В общем случае следствием достижения предельного состояния изнашивающихся деталей и их сопряжений могут быть функциональные нарушения, увеличение энергетических потерь и снижение КПД, уменьшение прочности и жесткости деталей, возникновение ошибок положений деталей в результате изнашивания сопряженных деталей узла трения.
Важность поиска оптимальной величины предельного износа обусловлена, с одной стороны, неоправданным уменьшением срока службы деталей при ее занижении, а с другой – повышением текущих затрат из-за аварийных ремонтов при ее завышении. В настоящее время имеется несколько критериев оценки величины предельного износа в зависимости от вида узла трения и типа сопряжения: по потере прочности детали, по снижению производительности и увеличению энергоемкости, по нарушению нормального взаимодействия деталей (в зубчатых передачах, в шарнирных соединениях) или по невыполнению заданных функций.
Предельный износ элементов может быть установлен из условия обеспечения их нормальной работы или других ограничений. В качестве примера таких ограничений для рабочих органов можно привести уменьшение зубьев ковша на половину их длины, уменьшение длины ножей отвала бульдозера на величину, определяемую началом изнашивания рамы, и др. Кроме того, установление величин предельного износа имеет существенное значение при выборе такого конструктивного параметра деталей узлов трения и элементов рабочего оборудования как толщина упрочненного (тем или иным методом) слоя на поверхности детали с учетом запаса на износ.
Не менее важное значение имеет оценка скоростей изнашивания деталей узлов трения и элементов рабочего оборудования. В настоящее время имеется большой экспериментальный материал о динамике изнашивания с описанием процесса различными эмпирическими уравнениями. Среднюю скорость изнашивания определяют различными методами, отличающимися подходом к оценке основных параметров трения и их связи со скоростью изнашивания. Один из них связывает скорость изнашивания с мощностью процесса трения и площадью фрикционного контакта. В этом случае среднюю скорость изнашивания элементов рабочего оборудования в абразивной среде можно определить по формуле
 ,
,
где a – коэффициент износа (коэффициент пропорциональности);
 – средняя мощность трения;
– средняя мощность трения;
К абр – коэффициент абразивности среды (К абр = 1…6);
F – площадь трения (площадь контакта трущихся элементов);
εи – относительная износостойкость трущегося элемента (εи = 1,0…2,2)
Среднюю мощность трения находят из выражения
 ,
,
где f – коэффициент трения между рабочим органом и средой;
P – нормальная сила, действующая в зоне трения;
v – скорость относительного движения.
Формулу для определения средней скорости изнашивания элементов рабочего оборудования в абразивной среде можно также использовать для оценки скорости изнашивания трущихся поверхностей в узле трения в случае контактно-абразивного изнашивания. Оно возникает в сопряжениях при наличии в смазочном материале большого количества абразива (более 3 масс. %). При этом износостойкость εи детали в основном определяется твердостью материала Н, из которого она изготовлена,

где Н эт – твердость материала эталонной детали.
При оценке надежности деталей узлов и агрегатов дорожно-строительных, путевых, подъемно-транспортных и других машин наибольший интерес представляют детали и элементы трансмиссий (зубчатые колеса, валы, подшипники и др.).
Надежность зубчатых передач. Значительную часть цилиндрических зубчатых колес используют в приводах упомянутых машин для передачи больших мощностей в условиях воздействия динамических нагрузок. Поэтому оценка их надежной работы и прогнозирование ресурса имеют актуальное значение как на этапе проектирования, так и на этапе их эксплуатации.
Вероятность безотказной работы по критерию контактной прочности определяют как вероятность того, что расчетные контактные напряжения σ Н не превышают предела контактной выносливости σ Н lim. Ее определяют в зависимости от квантили up нормального распределения разности этих напряжений из выражения
 ,
,
где  – дисперсия предела контактной выносливости;
– дисперсия предела контактной выносливости;
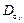 – дисперсия контактного напряжения.
– дисперсия контактного напряжения.
Как уже отмечалось, в инженерной практике нередко более удобно пользоваться оценкой величины квантили через коэффициент запаса прочности (безопасности) n п, связывающий значения предела выносливости σ Н lim и контактных напряжений σ Н l. Если в формулу для определения квантили up подставить его среднее значение 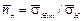 и ввести коэффициенты вариации величин σ Н lim и σ Н (соответственно
и ввести коэффициенты вариации величин σ Н lim и σ Н (соответственно  и
и  ), то она будет выглядеть следующим образом
), то она будет выглядеть следующим образом
 .
.
Как известно, выход из строя зубчатых передач обусловлен усталостными процессами, которые развиваются и накапливаются при циклическом контакте зубьев колеса и шестерни. Поэтому основным расчетом при оценке прочностных параметров зубчатых передач является расчет на контактную прочность.
Величину контактных напряжений в прямозубой цилиндрической зубчатой передаче внешнего зацепления можно рассчитать по формуле
 ,
,
где ZH – коэффициент, учитывающий форму сопряженных поверхностей зубьев (ZH = 1,77);
ZM – коэффициент, учитывающий механические свойства материала сопряженных колес (ZM = 190 МПа–1/2);
Z Σ – коэффициент, учитывающий суммарную длину контактных линий (Z Σ = 0,9);
КН = КН α КН β КНv – коэффициент нагрузки;
КН α – коэффициент, учитывающий распределение нагрузки между зубьями (для прямозубых передач КН α = 1);
КН β – коэффициент, учитывающий неравномерность распределения нагрузки;
КНv – коэффициент, учитывающий динамическую нагрузку;
 – окружная сила, Н;
– окружная сила, Н;
 – крутящий момент на валу шестерни, Н×м;
– крутящий момент на валу шестерни, Н×м;
 – делительный диаметр шестерни, мм;
– делительный диаметр шестерни, мм;
 – рабочая ширина зубчатого венца, мм;
– рабочая ширина зубчатого венца, мм;
 – передаточное число;
– передаточное число;
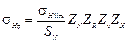 – допускаемое контактное напряжение (меньшее из напряжений для шестерни и колеса), МПа;
– допускаемое контактное напряжение (меньшее из напряжений для шестерни и колеса), МПа;
 – коэффициент безопасности (запаса прочности)
– коэффициент безопасности (запаса прочности)
SN = 1,10…1,25 – для колес без упрочения;
SN = 1,20…1,35 – для колес с упрочнением;
ZN – коэффициент долговечности (ZN = 0,9…1,0 для постоянного режима работы);
ZR – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев (ZR = 0,9…1,0);
Zv – коэффициент, учитывающий окружную скорость;
ZX – коэффициент, учитывающий размер зубчатого колеса (ZX = 1,0 для колес с диаметром менее 700 мм).
Как правило, принимают ZNZRZvZX = 0,9.
Взаимосвязь допускаемого контактного напряжения σ Нр с долговечностью колес зубчатой передачи устанавливают коэффициентом ZN, величина которого зависит от числа циклов напряжения NK в соответствии с заданным сроком службы и базовым числом циклов перемены напряжений NH lim.
При постоянной нагрузке NK, равное суммарному числу циклов перемены напряжений, определяют из выражения
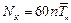 ,
,
где n – частота вращения вала шестерни, мин–1;
 – средний заданный ресурс передачи, ч.
– средний заданный ресурс передачи, ч.
При переменной нагрузке вместо NK используют эквивалентное число циклов перемены напряжений, зависящее от циклограммы нагружения.
При оценке вероятности неразрушения детали зубчатой передачи расчет ведут по величине квантили up с учетом рассеяния действующего контактного напряжения σ Н как функции комплексного коэффициента нагрузки КН (случайной величины) и предела контактной выносливости зубьев σ Н lim как функции твердости зубьев, которая также является случайной величиной. Для этого следует:
1) оценить величину вариации коэффициента нагрузки КН = КН α КН β КНv и определить коэффициент вариации контактного напряжения νσ H;
2) рассчитать коэффициент вариации νσ Hl предела контактной выносливости зубьев;
3) определить величину квантили;
4) оценить вероятность неразрушения детали, исходя из величины квантили, для рассчитанных контактных напряжений и их рассеяния.
Величину вариации ν Н Σ коэффициента КН можно определить как сумму независимых величин вариации коэффициентов КН α, КН β и КНv из выражения
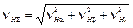 ,
,
где  – коэффициент вариации нагрузки между зубьями, оцениваемой величиной КН α,
– коэффициент вариации нагрузки между зубьями, оцениваемой величиной КН α,
 ;
;
 – коэффициент вариации нагрузки по ширине зубчатого венца, выраженной через КН β,
– коэффициент вариации нагрузки по ширине зубчатого венца, выраженной через КН β,
 ;
;
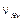 – коэффициент вариации динамической нагрузки в зацеплении, характеризуемой величиной КН ν,
– коэффициент вариации динамической нагрузки в зацеплении, характеризуемой величиной КН ν,
 ,
,
 ,
,  и
и  – соответственно средние значения коэффициентов КН α, КН β и КН ν.
– соответственно средние значения коэффициентов КН α, КН β и КН ν.
Далее следует определить коэффициент вариации  расчетного контактного напряжения σ Н (с учетом величины коэффициента вариации ν Н Σ):
расчетного контактного напряжения σ Н (с учетом величины коэффициента вариации ν Н Σ):
 .
.
При оценке коэффициента вариации νσ Hl предела выносливости следует учитывать величину коэффициента вариации базового предела контактной выносливости  :
:
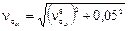 ,
,
где для зубьев без термообработки  ;
;
для упрочненных зубьев  .
.
Далее, имея известные значения  и
и  , а также величину
, а также величину 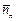 , определяют величину квантили up, после чего оценивают показатель надежности детали, а именно вероятность ее безотказности для данного уровня контактных напряжений и степени их рассеяния.
, определяют величину квантили up, после чего оценивают показатель надежности детали, а именно вероятность ее безотказности для данного уровня контактных напряжений и степени их рассеяния.
Надежность валов. Для большинства валов современных машин решающую роль в обеспечении их долговечности имеет сопротивление усталости. Проверка обеспечения требований к их долговечности по критерию усталости включает составление расчетной схемы, построение эпюр изгибающих и крутящих моментов, а также определение величины этих моментов в опасных сечениях вала.
В процессе нагружения вал подвергается действию взаимосвязанных нормальных и касательных напряжений, которые образуют несколько опасных зон, распределенных по длине вала. Нормальные напряжения, как известно, значительно превосходят касательные.
При длительных нагрузках принимают стационарный характер нагруженности вала, при котором амплитуда напряжений в процессе нагружения мало изменяется.
Основными нагрузками для большинства валов являются силы от зубчатых колес, звездочек, шкивов, а также от муфт из-за несоосности соединяемых муфтами деталей.
При расчетах на выносливость наибольшее значение имеют изгибающие моменты М и a, поэтому опасные сечения находятся в области их действия в сочетании с источником концентрации напряжений.
Для переменного режима действия длительных нагрузок в расчетах используют приведенную (по долговечности) амплитуду нормальных (σ а пр) и касательных (τ а пр) напряжений:
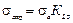 ;
;  ,
,
где σ a = (σmax – σmin)/2, τ a = (τmax – τmin)/2 – амплитуды цикла нормальных и касательных напряжений соответственно;
 ,
,
 – коэффициенты долговечности по нормальным и касательным напряжениям соответственно;
– коэффициенты долговечности по нормальным и касательным напряжениям соответственно;
Ni, N б – соответственно общее число циклов при напряжении σ ai (τ ai) и базовое число циклов (в точке перелома кривой усталости);
m – показатель степени кривой усталости (m = 6…10).
Общий запас прочности по пределу выносливости при совместном действии изгиба и кручения
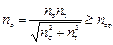 ,
,
где  – запас усталостной прочности по изгибу;
– запас усталостной прочности по изгибу;
 – предел выносливости вала по изгибу в данном сечении;
– предел выносливости вала по изгибу в данном сечении;
σиlim – предел выносливости материала вала по изгибу;
 – коэффициент асимметрии цикла напряжений по изгибу для данного сечения вала;
– коэффициент асимметрии цикла напряжений по изгибу для данного сечения вала;
ψσ – коэффициент асимметрии цикла напряжений по изгибу;
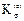 – коэффициент концентрации напряжений по изгибу для данного сечения вала;
– коэффициент концентрации напряжений по изгибу для данного сечения вала;
σ m = (σmax – σmin)/2 – среднее значение напряжения изгиба;
 – запас усталостной прочности по кручению;
– запас усталостной прочности по кручению;
 – предел выносливости материала вала по кручению в данном сечении;
– предел выносливости материала вала по кручению в данном сечении;
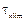 – предел выносливости материала вала по кручению;
– предел выносливости материала вала по кручению;
 – коэффициент асимметрии цикла напряжений по кручению для данного сечения вала;
– коэффициент асимметрии цикла напряжений по кручению для данного сечения вала;
ψτ – коэффициент асимметрии цикла напряжений по кручению;
 – коэффициент концентрации напряжений по кручению для данного сечения вала;
– коэффициент концентрации напряжений по кручению для данного сечения вала;
τ m = (τmax – τmin)/2 – среднее значение напряжения кручения;
n ор – допускаемая величина запаса прочности (n ор = 1,5…3).
Вероятность безотказной работы вала по критерию усталостной выносливости оценивают в зависимости от величины квантили нормального закона распределения нагрузки и предела выносливости вала в заданных ранее сечениях.
При расчетах следует учитывать основные факторы, влияющие на долговечность вала. К ним относятся статические и усталостные характеристики металла, его напряженные состояние, изменение предела выносливости из-за концентрации напряжений и влияния размеров вала, качества обработки поверхностей и метода поверхностного упрочнения.
Расчет вероятности неразрушения вала ведут способом, аналогичным используемому для оценки вероятности неразрушения детали зубчатой передачи.
Как отмечалось, нормальные и касательные напряжения взаимосвязаны, причем нормальные напряжения существенно выше касательных. Поэтому коэффициент вариации нагрузки принимают общим.
Нагрузочный режим оценивают по нормальным напряжениям (при изгибе) через коэффициент вариации нагрузки, который, в свою очередь, зависит от коэффициента концентрации нагрузки и коэффициента асимметрии цикла. Коэффициент концентрации нагрузки принимают  ; коэффициент асимметрии цикла принимают νψσ = 0,12…0,15. Суммарный коэффициент вариации нагрузки вала
; коэффициент асимметрии цикла принимают νψσ = 0,12…0,15. Суммарный коэффициент вариации нагрузки вала  . Тогда коэффициент вариации напряжений при изгибе, определяющих кинетику усталостных процессов, νиσ = 0,5νσΣ.
. Тогда коэффициент вариации напряжений при изгибе, определяющих кинетику усталостных процессов, νиσ = 0,5νσΣ.
Оценку коэффициента вариации предела выносливости вала по изгибу производят по формуле
 ,
,
где  – коэффициент вариации длительного предела выносливости базового образца;
– коэффициент вариации длительного предела выносливости базового образца;
 ,
,  – коэффициенты вариации предела выносливости соответственно детали из металла данной плавки
– коэффициенты вариации предела выносливости соответственно детали из металла данной плавки  и между плавками
и между плавками 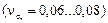 ;
;
 – коэффициент вариации параметра концентрации напряжений;
– коэффициент вариации параметра концентрации напряжений;
ν р – коэффициент вариации размерных параметров при изготовлении кольцевой выточки (или галтели) (ν р = 0,08…0,10).
Запас прочности  определяют по средним напряжениям при изгибе из выражения
определяют по средним напряжениям при изгибе из выражения

где  ;
;
 – предел прочности металла;
– предел прочности металла;
 – средняя амплитуда цикла;
– средняя амплитуда цикла;
 – средний изгибающий момент от переменных нагрузок;
– средний изгибающий момент от переменных нагрузок;
W и – момент сопротивления сечения вала при изгибе ( );
);
 – среднее напряжение цикла;
– среднее напряжение цикла;
 – средний изгибающий момент от постоянных нагрузок.
– средний изгибающий момент от постоянных нагрузок.
Надежность подшипников качения. Для подшипников качения расчеты на долговечность были первыми вероятностными расчетами деталей машин. Для них накоплен обширный материал испытаний, изучена их работоспособность в различных условиях нагружения, на базе чего составлен каталог данных по параметрам нагрузки и долговечности. Однако в этих расчетах учитывалось рассеяние только динамической грузоподъемности подшипников, предполагая детерминированную расчетную нагрузку.
В вероятностных расчетах динамическую эквивалентную нагрузку Р также рассматривают как случайную величину. В этом случае вероятность безотказной работы подшипника качения отождествляют с вероятностью выполнения условия
 ,
,
где L – номинальная долговечность (ресурс);
[ c ] – динамическая грузоподъемность по каталогу;
m – показатель степени (m = 3 для шарикоподшипников, m = 10/3 для роликоподшипников).
Отметим, что паспортная грузоподъемность [ c ] – это постоянная нагрузка, которую подшипник может выдержать в течение 106 оборотов без проявления усталостных разрушений не менее чем у 90 % подшипников, поставленных на испытания. 90 %-ную динамическую грузоподъемность, представленную в каталогах, обозначают С 90.
Ресурс подшипников (в часах) можно определить из выражения
 ,
,
где n – частота вращения, мин–1.
Величину эквивалентной динамической нагрузки определяют в зависимости от типа подшипника по следующим формулам:
для радиальных шариковых и радиально-упорных подшипников –
 ;
;
для радиальных роликоподшипников (двух- и однорядных с короткими цилиндрическими роликами, не обладающими осевой грузоподъемностью) –
 ;
;
для шариковых и роликовых упорных подшипников –
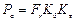 ;
;
для радиально- упорных подшипников –
 ;
;
для упорных сферических подшипников –
 ,
,
где Pr, Pa – соответственно эквивалентные динамические радиальная и осевая нагрузки;
Fr, Fa – соответственно радиальная и осевая нагрузки;
V – коэффициент учета вращения элементов подшипника, V = 1,0 (при вращении внутреннего кольца), V = 1,2 (при вращении наружного кольца);
X, Y – коэффициенты соответственно радиальной и осевой нагрузок, принимаемые по каталогам;
К б – коэффициент безопасности, учитывающий характер нагрузки;
К т – температурный коэффициент.
При оценке надежности подшипников качения предполагают, что динамическая эквивалентная нагрузка и динамическая грузоподъемность распределены по нормальному закону, а при определении вероятности неразрушения подшипников качения исходят из того, что и динамическая эквивалентная нагрузка, и динамическая грузоподъемность являются величинами случайными, рассеяние которых учитывают соответствующими коэффициентами вариации.
Коэффициент вариации ν р динамической эквивалентной нагрузки принимают равным коэффициенту вариации внешней нагрузки, действующей на подшипник (ν р = 0,12).
Коэффициент вариации ν с динамической грузоподъемности принимают равным: ν с = 0,25 – для роликоподшипников, ν с = 0,27 – для шарикоподшипников.
Запас прочности по средним нагрузкам
 ,
,
где  – среднее значение динамической грузоподъемности,
– среднее значение динамической грузоподъемности, 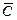 = 1,46 С 90 (для роликоподшипников),
= 1,46 С 90 (для роликоподшипников), 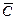 = 1,52 С 90 (для шарикоподшипников);
= 1,52 С 90 (для шарикоподшипников);
 – среднее значение динамической эквивалентной нагрузки, которую вычисляют по приведенным выше зависимостям, в которые подставляют средние значения радиальной и осевой нагрузок, действующих на подшипник.
– среднее значение динамической эквивалентной нагрузки, которую вычисляют по приведенным выше зависимостям, в которые подставляют средние значения радиальной и осевой нагрузок, действующих на подшипник.
Таким образом запас прочности по средним нагрузкам будет иметь следующий вид:
для шарикоподшипников –
 ,
,
для роликоподшипников –
 .
.
Подставляя приведенные значения