Составляющие надежности
Надежность – это свойство машины выполнять заданные функции, сохраняя во времени эксплуатационные показатели в заданных пределах в соответствии с режимом работы и условиями использования, технического обслуживания (ТО), текущего ремонта (ТР), хранения и транспортирования (ГОСТ 24.002–9). Уровень надежности машин оказывает существенное влияние на их эксплуатационные, технологические и технико-экономические показатели. Выбор оптимального уровня надежности машин является важной задачей, поскольку при недостаточной надежности резко возрастают затраты на техническое обслуживание и ремонт, а при избыточной – снижается эффективность их производственного использования и происходит перерасход ресурсов.
Надежность включает следующие свойства: безотказность, долговечность, ремонтопригодность и сохраняемость.
Безотказность – свойство машины непрерывно сохранять работоспособность в течение некоторой наработки (т. е. продолжительности или объема работ). Ее оценивают в единицах времени или в виде числа рабочих циклов.
Свойство безотказности проявляется в зависимости от назначения машины как при ее эксплуатации, так и в режиме ожидания работы.
Долговечность – свойство машины сохранять работоспособность до наступления предельного состояния при установленной системе ТО и ТР.
В отличие от безотказности свойство долговечности характеризует продолжительность работы машины по суммарной наработке, которая прерывается периодами для восстановления ее работоспособности в плановых и внеплановых ремонтах, при техническом обслуживании.
Ремонтопригодность – приспособленность машины к предупреждению и обнаружению причин возникновения ее отказов (повреждений) и устранению их последствий путем ТО и ТР.
|
|
Свойство ремонтопригодности количественно характеризует компоновку машины (ее агрегатов и сборочных единиц), а также их доступность и съемность при сборке и разборке.
Сохраняемость – свойство машины непрерывно сохранять исправное и работоспособное состояние в процессе хранения и транспортирования.
Свойство сохраняемости характеризует способность машины противостоять отрицательному влиянию факторов ее длительного хранения и транспортирования, а также обеспечить после этого ее применение с заданными функциональными параметрами при сохранении показателей безотказности и долговечности.
Для разных машин эти свойства имеют различную значимость. Для машин, отказ которых может повлечь крупные убытки от простоев (краны и другие ПТМ), наиболее важным свойством является их безотказность, а для транспортирующих машин – ремонтопригодность, поскольку непродолжительные отказы существенно не влияют на их производительность.
Наглядное представление о надежности машины дает график ее работы (рисунок 5.1), на котором представлены периоды наработки, ремонта и технического обслуживания, т. е. периоды работоспособного (наработка) и неработоспособного (простои в ремонте) состояния машины.
Эти периоды могут различаться по продолжительности и чередованию, что дает информацию о надежности машины. В частности длина участков t н характеризует ее безотказность: чем они длиннее, тем выше безотказность. Длина участков t р и t то свидетельствует о ремонтопригодности машины (с их уменьшением ремонтопригодность возрастает). И, наконец, с увеличением длины участков t н + t р и t н + t то растет долговечность машины.
|
|
Показатели надежности
Для решения практических задач по определению надежности машины используют многочисленные единичные и комплексные показатели, дающие количественную оценку одной или нескольких характеристик надежности. Из их числа следует выбрать такие показатели, которые в достаточно полной мере могут дать информацию о надежности. Эффективность эксплуатации машины в первую очередь зависит от показателей надежности, которые характеризуют длительность периодов эксплуатации, технического обслуживания и ремонта, а также затрат на поддержание работоспособного состояния при эксплуатации. Поэтому в качестве основных характеристик надежности целесообразно использовать следующие показатели: средний и гамма-процентный ресурсы до капитального ремонта или до списания; вероятность безотказной работы, средняя наработка до отказа или на отказ; интенсивность отказов или параметры потока отказов; среднее время восстановления работоспособного состояния; коэффициент технического использования и коэффициент готовности.
Из перечисленных характеристик к показателям надежности, присущим только восстанавливаемым элементам, следует отнести среднюю наработку на отказ, наработку между отказами, среднее время восстановления.
Ресурсные показатели характеризуют долговечность машин и их элементов. Статистическая оценка среднего ресурса до капитального ремонта (или до списания) при наличии сведений о ресурсах N машин выражается формулой
|
|
,
где Ti – величина ресурса машины.
Гамма-процентным ресурсом Tj считается наработка, в течение которой машина не достигает предельного состояния с заданной вероятностью j процентов (j, %), т. е. j (регламентированная вероятность) – это заданный процент машин, каждая из которых достигает установленного ресурса Tj. Он выражается зависимостью
.
Для j = 50 % ресурс называют медианным.
Следующая группа показателей характеризует безотказность машин. К ним относятся вероятность безотказной работы, наработка на отказ, среднее число отказов.
Вероятность безотказной работы – это вероятность того, что в пределах заданной наработки не произойдет отказа машины. При достаточно большом числе анализируемых машин статистическую вероятность безотказной работы можно оценить с помощью выражения
,
где N – общее число машин, работоспособных в начальный момент времени;
n – число машин, отказавших ко времени t.
Это выражение можно представить в виде
,
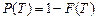где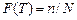 
– статистическая оценка вероятности отказа.
Наработка на отказ – это отношение наработки восстанавливаемой машины к математическому ожиданию (среднему значению) числа ее отказов в период этой наработки. Статистическая наработка на отказ восстанавливаемых машин
,
где 
– суммарная наработка восстанавливаемых машин,
N 0 – суммарное число их отказов.
Параметр потока отказов зависит от периодов работы до отказа и восстановления. Он характеризует среднее число отказов восстанавливаемой машины за заданное время наработки
,
где n (t) – число отказов за промежуток времени 
;
Σ ti – наработка за тот же промежуток времени.
В число показателей безотказности невосстанавливаемых деталей и узлов машин входят вероятность безотказной работы, средняя наработка до отказа и интенсивность отказов.
Средняя наработка до отказа – это математическое ожидание наработки до первого отказа. Эта характеристика невосстанавливаемых элементов соответствует показателю средней наработки на отказ восстанавливаемых элементов. Статистически наработку до отказа определяют из выражения
,
где t 1 i – наработка до первого отказа i- го изделия;
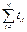– суммарная наработка неремонтируемых элементов до отказа;
N – общее число этих элементов.
Интенсивность отказов λ(t) – это вероятность отказа невосстанавливаемого элемента, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник, т. е. это число отказов Δ n, происшедших в единицу времени Δ t, начиная с момента времени t, отнесенное к числу элементов, работоспособных в этот момент. Статистическая оценка λ(t) может быть выражена в виде
,
где N р – число работоспособных элементов.
Как правило, для многих элементов машин зависимость интенсивности отказов (или опасности отказа) от времени наработки имеет вид, представленный на рисунке 5.2.
Время наработки можно условно разбить на три этапа. На первом этапе, который характеризуется повышенной интенсивностью отказов, происходит приработка и выявление скрытых дефектов, как конструктивных, так и технологических. Часто окончание приработочного этапа связывают с завершением гарантийного обслуживания машин заводом-изготовителем. На втором этапе реализуется режим стабильной работы, для которого характерна постоянная интенсивность отказов, которые носят случайный характер и появляются внезапно от действия случайных факторов. При этом время появления отказов не связано с предыдущей наработкой. И, наконец, на третьем этапе – этапе усиленного старения – происходит увеличение интенсивности отказов вплоть до достижения предельного состояния из-за массового числа отказов вследствие усиленного износа, усталостного разрушения и других причин, связанных с длительной эксплуатацией. Ресурс машины назначают, как правило, в конце второго – начале третьего этапов наработки.
Среднее время восстановления работоспособного состояния (математическое ожидание времени восстановления работоспособности) относится к показателям ремонтопригодности машин и их элементов. Оно характеризует продолжительность вынужденного простоя, необходимого для поиска причины отказа. Статистически среднее время восстановления определяют по формуле
где N – общее число восстанавливаемых машин;
t в i – время восстановления i -й машины.
Помимо указанных единичных показателей, характеризующих одно из свойств надежности, используют комплексные показатели, которые позволяют одновременно оценить несколько характеристик надежности машины. К ним относят коэффициенты технического использования и готовности.
Коэффициент технического использования k ти статистически определяют отношением суммарного времени пребывания машин в работоспособном состоянии к суммарному времени их эксплуатации, включающем периоды пребывания машины в работоспособном состоянии и периоды простоев:
,
где t н – суммарная наработка (пребывание в работоспособном состоянии) всех машин;
t р – суммарное время простоев при проведении плановых и внеплановых ремонтов всех машин;
t то – суммарное время простоев при проведении всех видов технического обслуживания машин;
t в – суммарное время восстановления работоспособности машин.
Коэффициент готовности k г характеризует вероятность того, что машина окажется работоспособной в произвольный момент времени, кроме периодов выполнения планового технического обслуживания. Статистически k г определяют отношением времени безотказной работы к сумме времени безотказной работы и времени простоя (за исключением периодов времени плановых ремонтов и технического обслуживания):
,
где Т о – среднее время безотказной работы (наработка на отказ);
Т в – среднее время восстановления.
Как видно из данного выражения, коэффициент готовности дает информацию о таких единичных показателях как наработка на отказ, характеризующая безотказность, и среднее время восстановления, которое характеризует эксплуатационную технологичность и ремонтопригодность.
Из определений k ти и k г следует, что чем меньше среднее время восстановления и суммарные простои, связанные с техническим обслуживанием и ремонтом, тем выше 
и 
.
Основные распределения случайных величин, используемые при оценке надежности
Основные показатели надежности, а также характеристики режимов нагружения машин и другие параметры являются случайными величинами, которые могут быть непрерывного или дискретного типа. Значения случайных величин могут повторяться с частотой, определяемой функцией распределения F (t) = P (T < t) и плотностью распределения f (t) = F '(t), где t – значение случайной величины Т.
Для решения ряда практических задач достаточно характеризовать распределение случайной величины рядом основных числовых характеристик (рисунок 5.3). К ним относятся математическое ожидание (среднее значение), дисперсия или среднее квадратическое отклонение, коэффициент вариации, мода, медиана и квантиль. Последние характеризуют положение центров группирования случайных величин на числовой прямой. Эти характеристики используют как при статистической обработке результатов, так и в вероятностных расчетах при прогнозировании надежности.
Математическое ожидание (среднее значение) m (t) является основной характеристикой случайной величины. Это постоянное число, к которому устойчиво приближается с ростом числа испытаний арифметическое значение случайной величины, найденное по опытным данным. Значение математического ожидания, определяемое по результатам наблюдений или испытаний (как для дискретных, так и для непрерывных величин), называют статистической оценкой математического ожидания или оценкой среднего арифметического значения
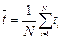
или
,
где N – общее число наблюдений (значений случайной величины);
ti – текущее значение случайной величины;
gi – число одинаковых значений ti.
При достаточно большом числе наблюдений полагают, что 
.
В вероятностных расчетах математическое ожидание определяют в зависимости от плотности распределения f (t) (для непрерывных величин) или вероятности Pi появления значения ti (для дискретных величин) из выражений
и
.
Дисперсией случайной величины называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания. Она характеризует разброс (рассеяние) случайной величины. Оценка дисперсии случайной величины – это среднее значение квадрата разности между текущим значением случайной величины и ее средним значением:
или
.
В вероятностных расчетах дисперсию оценивают по следующим выражениям:
– для дискретных случайных величин –
;
– для непрерывных случайных величин –
.
Поскольку дисперсия имеет размерность квадрата случайной величины, для удобства принято использовать характеристику, совпадающую по размерности со случайной величиной. Ее называют среднеквадратическим отклонением случайной величины. Она представляет собой корень квадратный из дисперсии, т. е.
.
Для оценки разброса случайных величин используют также коэффициент вариации (безразмерный показатель), равный отношению среднеквадратического отклонения к математическому ожиданию случайной величины
.
Модой случайной величины называют ее наиболее вероятное значение или то значение, при котором плотность вероятности максимальна.
Медиана характеризует расположение центра группирования случайной величины. Площадь под кривой f (t) делится медианой пополам (см. рисунок 5.3).
Квантилью называют значение случайной величины, соответствующее заданной вероятности. Квантиль, соответствующую вероятности 0,5, называют медианой.
В теории надежности применяют ряд законов распределения случайных величин. Выбор того или иного закона обусловлен характером изменения надежности машин, особенностями проявления отказов. Для инженерных расчетов наиболее часто используют экспоненциальное, нормальное и распределение Вейбулла.
Экспоненциальное распределение применяют для положительных непрерывных случайных величин. В общем случае его можно представить в виде
,
где P (t) – вероятность того, что случайная величина имеет значение, большее t;
λ – параметр распределения.
Если в качестве переменной t используют время, закон экспоненциального распределения считают основным уравнением надежности, которое характеризует вероятность безотказной работы. P (t) называют также функцией надежности.
Экспоненциальное распределение применяют для описания отказов агрегатов, узлов и машин, эксплуатирующихся в тяжелых условиях, в частности, строительных и дорожных машин. Его широко используют для изучения внезапных отказов, которые вызваны неблагоприятным стечением обстоятельств и поэтому имеют постоянную интенсивность независимо от срока службы машины.
Следует отметить, что решение задач надежности при использовании экспоненциального закона оказывается намного проще, чем при использовании других законов распределения. Это связано с тем, что при экспоненциальном законе вероятность безотказной работы зависит только от длительности периода и не зависит от времени предыдущей работы.
При описании внезапных отказов из закона экспоненциального распределения можно определить вероятность безотказной работы, которая одинакова за любой равный промежуток времени в период нормальной эксплуатации машины.
Для экспоненциального распределения функции вероятности отказа F (t), плотности вероятности отказа f (t) и интенсивности отказов λ(t) имеют следующий вид:
;
;
.
Среднее время до возникновения отказа можно определить из выражения
.
Экспоненциальное распределение является однопараметрическим, определяемое только параметром λ. Для его определения достаточно получить оценку средней наработки до отказа Т 1. На рисунке 5.4 представлены зависимости параметра λ(t), а также P (t) и f (t).
Нормальное распределение (распределение Гаусса) применяют для любых непрерывных случайных величин. Оно является наиболее универсальным и используется для описания постепенных отказов. Для нормального распределения плотность вероятности отказа, вероятность отказа и вероятность безотказной работы (функцию надежности) можно определить по формулам
,
,
.
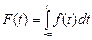Нормальное распределение имеет два независимых параметра: математическое ожидание, или среднюю наработку на отказ, и среднеквадратическое отклонение.
Особенностью нормального распределения является ограниче-ние подавляющего большинства отклонений от математического ожидания интервалом ±3 S.
Распределение Вейбулла также является наиболее распростра-ненным. Его используют для описания наработки деталей по усталостным разрушениям, а также для оценки надежности деталей и узлов дорожно-строительной, подъемно-транспортной и другой техники, в частности времени их безотказной работы, времени наработки до предельного состояния. Это распределение является универсальным, так как при соответствующих значениях параметров превращается в нормальное, экспоненциальное и другие виды распределения.
В основном используют двухпараметрическое распределение, для которого плотность распределения описывается зависимостью
,
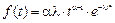где α – параметр формы кривой распределения;
λ – параметр масштаба.
На рисунке 5.6 представлена зависимость плотности распределения при λ = 1.
Функции распределения Вейбулла и вероятности безотказной работы имеют вид
,
.
В этом случае выражение для расчета математического ожидания принимает вид
,
где Г (t) – гамма-функция.
Значения параметров определяют по специальным таблицам в зависимости от оценки коэффициента вариации.
Распределение Вейбулла имеет более широкие возможности и позволяет получить лучшее соответствие расчетных значений экспериментальным или опытным данным по сравнению с экспоненциальным распределением.
При значениях параметра α < 1 это распределение используют для описания надежности детали на этапе приработки. Если α > 1, его можно использовать для описания надежности деталей при быстром старении. При α = 3,3 распределение Вейбулла близко к нормальному.
Следует отметить, что при решении задач по оценке надежности не обязательно знать упомянутые аналитические зависимости этого распределения, а также их коэффициенты вариации, поскольку все необходимые расчетные данные с использованием закона Вейбулла табулированы.