Раздел 2. Тепломассообмен.

Раздел 1. Термодинамика.

Задача № 1.

Объёмный состав горючего газа: r_СО = 11%; r _{Н 2} = 47%; r_СН4 = 30%; r_С2Н4 = 5%; r_СО2 = 4%; r_N2 = 4%.

Определить кажущуюся мольную массу, плотность, удельный объем при нормальных условиях, массовую газовую постоянную R,парциальное давление метана в процентах и массовые доли содер­жания компонентов.

 

Дано: rСО = 11%; rН2 = 47%; rСН4 = 30%; rС2Н4 = 5%; rСО2 = 4%; rN2 = 4%.

Найти: μ_см.; (ρ_см.)_н.; υ_см.; R _см.; p_СН4; g_СО ; g_Н2 ; g _С2Н4 ; g _СН4 ; g _N2; g _СО2 –?

 

Решение:

1) Молекулярная масса смеси

μ_см = ∑ r_іμ_і = r_co μ_СО+ r_co μ _Н2 + r_co μ_СН4 + r_co μ_С2Н4 + r_co μ_СО2 + r_co μ_N2 = 0,11 · 28 + 0,47 · 2 + 0,30 · 16 + 0,05 · 28 + 0,04 · 44 + 0,04 · 28 =

= 3,08 + 0,94 + 4,8 + 1,4 + 1,12 = 11,34 кг/кмоль

 

2) Плотность каждого газа составляет

ρі = μі /22,4

ρ_СО = 28÷22,4=1,25 кг/м³

ρ _Н2 = 2 ÷22,4=0,09 кг/м³

ρ _СН4 = 16÷22,4=0,71 кг/м³

ρ _С2Н4 = 28÷22,4=1,25 кг/м³

ρ _СО2 = 44÷22,4=1,96 кг/м³

ρ _СО2 = 28÷22,4=1,25 кг/м³

(ρ_см.)_н = ∑ ρі · gі

ρ_см. = μ_см /22,4

ρ_см. = 11,34÷ 22,4=0,506 кг/м³

3) Удельный объем при нормальних физических условиях составляет

 

υ_см = 1/ρ_см = 1/0,506 = 1,976 м³/кг

 

4) Газовая постоянная смеси

 

R _см = μ R/ μ_см = 8314 /11,34 = 733,16 Дж/(кг·К)

 

5) Парциальное давление метана в процентах:

p_СН4 = r_СН4p_{см .}= 0,30 р = 30%

 

6) Массовая доля каждого из компонентов:

g_і = r_і (μ_і / μ_см)

g_СО = 0,11(28 / 11,34) = 0,27

g_Н2 = 0,47 (2 / 11,34) = 0,083

g _СН4 = 0,30 (16 / 11,34) = 0,423

g _С2Н4 = 0,05 (28 / 11,34) = 0,123

g _СО2 = 0,04 (44 / 11,34) = 0,155

g _N2 = 0,04 (28 / 11,34) = 0,099

 

Ответ : μ_{см .}= 11,34 г/моль; (ρ_см.)_н. = 0,506 кг/м³; υ_см = 1,976 м³/кг;

R _см = 733,16 Дж/(кг·К) или 0,733 кДж/(кг·К); p_СН4 = 30%; g_СО = 0,27; g_Н2 = 0,083; g _СН4 = 0,423; g _С2Н4 = 0,123; g _СО2 = 0,155; g _N2 = 0,099.

 

 

Задача № 2.

Воздух в количестве 1 кг последовательно меняет свое состояние следу-ющим образом (см. рис.): сначала, имея параметры р₁ = 0,26 МПа и t₁ = 40°С, изобарно расширяется до объема υ₂=2,80 υ_1,затем адиабатно сжимается до состояния при р₃ = 2МПа и, наконец, изотермически расширяется до υ₄=υ_2. Определить недостающие параметры во всех характерных точ­ках процессов, подведенную или отведенную теплоту, изменение внутренней энергии и энтальпии, а также работу расширения (сжа­тия) в каждом процессе. Проверить уравнение первого закона тер­модинамики для совокупности процессов.

Теплоемкости с_ри с_υ считать не зависящими от температуры и для их расчета применить молекулярно-кинетическую теорию.

 

Дано: m = 1 кг. р1 = 0,26 МПа = 2,6 · 106 Па t1 = 40 °С = 313 К р = const υ2 = 2,80 υ1 р3 =2 МПа Т = const υ4 = υ2 .

 

Найти: с_р; с_υ; р_і; Vі; t_і; q; ∆u; ∆h_і; ι_і -?

Решение:

R_{возд .} = 8314 / μ

R_{возд .} = 8314 / 29 = 286,7 Дж/(кг·К)

с_р = (k / k-1) R, где k = 1,4

с_р = (1,4 / 1,4-1) 286,7 = 1003,45 Дж/(кг·К)

с_р = 1 / (k-1) R = 1/(1,4-1) 286,7 = 716,75 Дж/(кг· К)

 

 

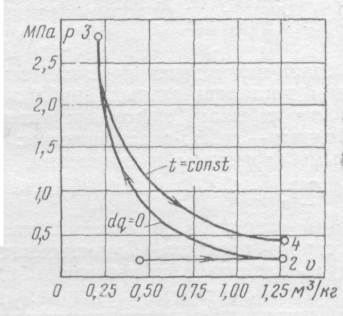
Параметры в точке 1

Из уравнения состояния р₁v₁= RТ₁

уделный объем равен v₁ = RТ₁/ р₁ = 286,7 · 313,15/(2,6· 10⁶) = 0,345 м³/кг

внутреняя энергия u₁= с_υ Т₁ = 716,75 · 313,15 = 224,45 кДж/кг

энтальпия h₁ = с_р Т₁ = 1003,45 · 313,15 = 314,23 кДж/кг

 

Параметры в точке 2

р₁ = р₂ = 0,26 МПа

υ ₂ = 2,80 · 0,345 = 0,97 м³/кг

Т₂ = (р₂υ ₂ ) / R =(0,26 · 10⁶ · 0,97) / 286,7 = 880 К = 605 °С

∆t = t₂ – t₁ = 605 – 40 = 565 °С

u₂ = с_υ Т₂ = 716,75 · 880 = 631 кДж/кг

h₂ = с_р Т₂ = 1003,45 · 880 = 883,036 кДж/кг

∆h = с_р ∆Т = 1003,45 · 565 = 566949,25 = 566,9 кДж/кг

Параметры в точке 3

показатель адиабаты k = с_р / с_υ = 1003,45 / 716,75 = 1,4

Так как Т₂ / Т₃ = (p₃ / p₂)^{(k-1) / k} то: Т₃ = Т₂ (p₂ / p₃)^{(k-1) / k}

Т₃ = 880 / (0,26/2)^{(1,4 -1) / 1,4} = 1895 К = 1620 °С

υ ₃ = (Т₃ R) / p₃ = (1895 · 286,7) / (2 · 10⁶ ) = 0,27 м³/кг

u₃ = с_υ Т₃ = 0,716 · 1895 = 1356,8 кДж/кг

h₃ = с_р Т₃ = 1003,45 · 1895 = 1901,44 кДж/кг

Параметры в точке 4

υ₄ = υ₂ = 0,97 м³/кг

Так как Т = const, тогда k = 1

p₃ / p₄ = υ ₄ / υ ₃

p₄ = (υ ₃ / υ ₄) p₃ = (0,27 / 0,97) · 2 = 0,5567 МПа

Т₄ = (p₄ υ ₄) / R = 1895 К = 1620 °С

u₄ = u₃ = 1356,8 кДж/кг

h₄ = h₃ = 1901,44 кДж/кг

Процесс 1 – 2:

Изменение внутренней энергии ∆ u_1-2 = u₂ – u₁ = 631 – 224,45 = 406,55 кДж/кг

подведенная теплота q_1-2 = ∆ h_1-2 + ι_техн. , где ι_техн = 0

q_1-2 = ∆ h_1-2 = 883,036 – 314,23 = 568,8 кДж/кг

работа изменения объема ι_1-2 = ∫ рdυ = р (υ ₂ – υ ₁) = 0,26 (0,97 – 0,345) = 162,5 кДж/кг

 

Процесс 2 – 3:

∆ u_2-3 = u₃ – u₂ = 1356,8 – 631 = 725,8 кДж/кг

∆ h = с_р ∆Т = 1003,45 (1620 – 605) = 1018501,7 Дж/кг = 1018,5 кДж/кг

q_2-3 = 0, тогда ι _{техн. 2-3} = – (h₃ – h₂)

техническая работа ι _{техн. 2-3} = 883,036 – 1901,44 = –1018,4 кДж/кг

работа изменения объема ι = ι _техн / k = –1018,4 / 1,4 = –727,4 кДж/кг

Процесс 3 – 4:

подведенная теплота q_3-4 = ι _техн.

q = ι = RТln (p₃/ p₄) = 286,7 · 1895 ln (2/0,5567) = 1951846 Дж/кг = 1951,8 кДж/к г

∆ u_3-4 = с_υ ∆Т = 0

∆ h_3-4 = с_р ∆Т = 0

Ответ:

Точки	р, МПа	υ, м3/кг	t, 0С	Т, К
	0,26	0,345		313,15
	0,26	0,97
		0,27
	0,5567	0,97
Процесс	q, кДж/кг	∆и, кДж/кг	∆h, кДж/кг	ι, кДж/кг
1-2 2-3 3-4	568,8 1951,8	406,55 725,8	566,9 1018,5	162,5 -727,4 1940,5
	2520,6	1132,35	1585,4	1375,6

Задача № 3.

Начальное состояние водяного пара задано температурой t₁ = 180 °С и степенью сухости х₁ = 0,76. Процесс подвода теплоты 1 – 2 происходит при p = const до температуры t₂ = 430 °С. В дальнейшем расширение происходит при t₂ = t₃ = 430 °С = const до тех пор, пока удельный объём не увеличивается до ν₃ = 0,6 м³/кг. Заключительный процесс 3 – 4 является изоэнтропным и пар расширяется до температуры в точке 4, равной t₄ = 30 °С.

Найти все недостающие параметры в каждой из характерных точек Т1, Т2, Т3, Т 4 (t _н; р; r; ν; ν'; ν"; ρ"; h; h'; h"; s; s'; s").

Представить процессы в hs - и Ts- диаграммах.

 

Дано: t1 = 180 °С - начальное состояние водяного пара х1 = 0,76 - степень сухости t2 = 430 °С - температура пара t2 = t3 = 430 °С t4 = 30 °С

 

Найти: точки Т1, Т2, Т3, Т 4 (р; r; ν; ν'; ν"; ρ"; h; h'; h"; s; s'; s").

 

Решение:

На hs-диаграмме для водяного пара находим точку Т1:

 

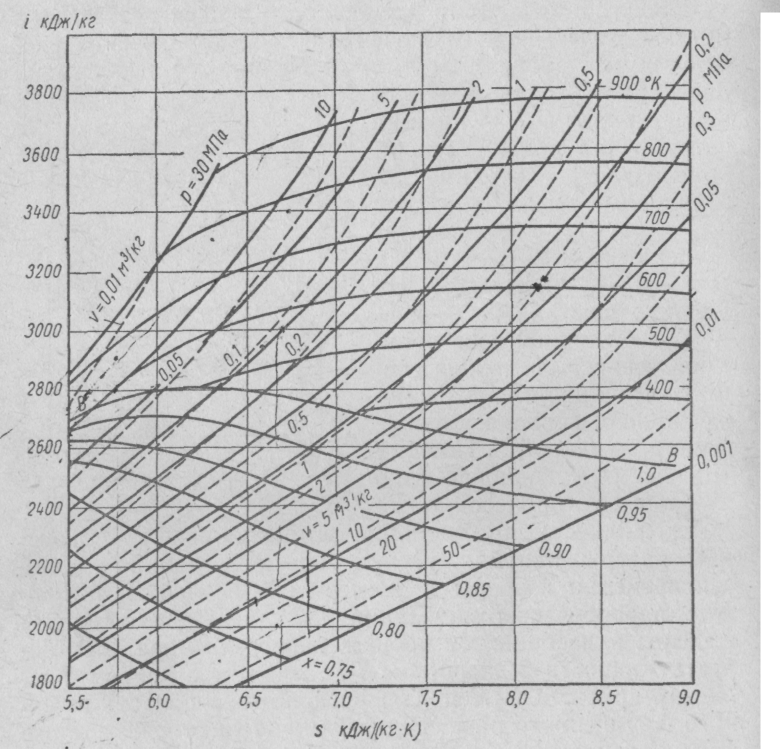
Остальные параметры находим по таблицам для насыщенного водяного пара по температуре и давлению (табл. XIII, XIV, стр.324-330, О.М. Рабинович, Сборник задач по технической термодинамике, 1973г.)

h = 3320 кДж/кг - энтальпия перегретого пара

h' = 763,1 кДж/кг - энтальпия насыщенной жидкости

h" = 2778 кДж/кг - энтальпия сухого насыщенного пара

s = 5,5 кДж/(кг·К) - энтропия пара

s' = 2,1395 кДж/(кг·К) - энтропия насыщенной жидкости (кипящей воды)

s" = 6,5858 кДж/(кг·К) - энтропия сухого насыщенного пара

р = 10 бар или 1 МПа - давление перегретого пара

ν = 0,18 м³/кг - удельный объём перегретого пара

ν' = 0,0011275 м³/кг - удельный объём кипящей воды

ν" = 0,1939 м³/кг - удельный объём сухого насыщенного пара

r = 2015 кДж/кг - скрытая теплота парообразования

ρ" = 5,157 кг/м³ - плотность жидкости

 

На hs -диаграмме для водяного пара находим точку Т2:

 

Остальные параметры также, как и для точки Т1, находим по таблицам для насыщенного водяного пара по температуре и давлению (табл. XIII, XIV, стр.324-330, О.М. Рабинович, Сборник задач по технической термодинамике, 1973г.)

h = 3330 кДж/кг - энтальпия перегретого пара

h' = 763,1 кДж/кг - энтальпия насыщенной жидкости

h" = 2778 кДж/кг - энтальпия сухого насыщенного пара

s = 7,55 кДж/(кг·К) - энтропия пара

s' = 2,1395 кДж/(кг·К) - энтропия насыщенной жидкости (кипящей воды)

s" = 6,5858 кДж/(кг·К) - энтропия сухого насыщенного пара

р = 10 бар или 1 МПа - давление перегретого пара

ν = 0,35 м³/кг - удельный объём перегретого пара

ν' = 0,0011275 м³/кг - удельный объём кипящей воды

ν" = 0,1939 м³/кг - удельный объём сухого насыщенного пара

r = 2015 кДж/кг - скрытая теплота парообразования

ρ" = 5,157 кг/м³ - плотность жидкости

 

 

На hs -диаграмме для водяного пара находим точку Т3:

 

По таблицам для насыщенного водяного пара находим остальные параметры для Т3:

 

h = 3320 кДж/кг - энтальпия перегретого пара

h' = 640,1 кДж/кг - энтальпия насыщенной жидкости

h" = 2749 кДж/кг - энтальпия сухого насыщенного пара

s = 7,88 кДж/(кг·К) - энтропия пара

s' = 1,860 кДж/(кг·К) - энтропия насыщенной жидкости (кипящей воды)

s" = 6,822 кДж/(кг·К) - энтропия сухого насыщенного пара

р = 5 бар или 0,5 МПа - давление перегретого пара

ν = 0,8 м³/кг - удельный объём перегретого пара

ν' = 0,0010927 м³/кг - удельный объём кипящей воды

ν" = 0,3747 м³/кг - удельный объём сухого насыщенного пара

r = 2109 кДж/кг - скрытая теплота парообразования

ρ" = 2,669 кг/м³ - плотность жидкости

 

На hs -диаграмме для водяного пара находим точку Т4:

 

По таблицам для насыщенного водяного пара находим остальные параметры для Т4:

 

h = 2340 кДж/кг - энтальпия перегретого пара

h' = 101,04 кДж/кг - энтальпия насыщенной жидкости

h" = 2545 кДж/кг - энтальпия сухого насыщенного пара

s = 7,9 кДж/(кг·К) - энтропия пара

s' = 0,3546 кДж/(кг·К) - энтропия насыщенной жидкости (кипящей воды)

s" = 8,576 кДж/(кг·К) - энтропия сухого насыщенного пара

р = 0,03 бар или 0,003 МПа - давление перегретого пара

ν = 35 м³/кг - удельный объём перегретого пара

ν' = 0,0010028 м³/кг - удельный объём кипящей воды

ν" = 45,66 м³/кг - удельный объём сухого насыщенного пара

r = 2444 кДж/кг - скрытая теплота парообразования

ρ" = 0,02190 кг/м³ - плотность жидкости.

 

 

Задача № 4.

Температура сухого термометра равна t = 20 °С. А влагосодержание сухого воздуха d = 10 г/кг. Найти: t_м - температуру мокрого термометра; t_р - температуру точки росы; φ - относительную влажность; Р_п - парциальное давление водяных паров в воздухе; h - энтальпию влажного воздуха.

 

Дано: t с. в. = 20 °С d с. в. = 10 г/кг

 

Найти: t_м - температуру мокрого термометра;

t_р - температуру точки росы;

φ - относительную влажность;

Р_п - парциальное давление водяных паров в воздухе;

h - энтальпию влажного воздуха.

Решение:

Используя h, d -диаграмму влажного воздуха (,,Сборник задач по технической термодинамике,, Т.Н. Андрианова, рисунок 10.1., стр. 95), по известным нам данным найдем неизвестные параметры.

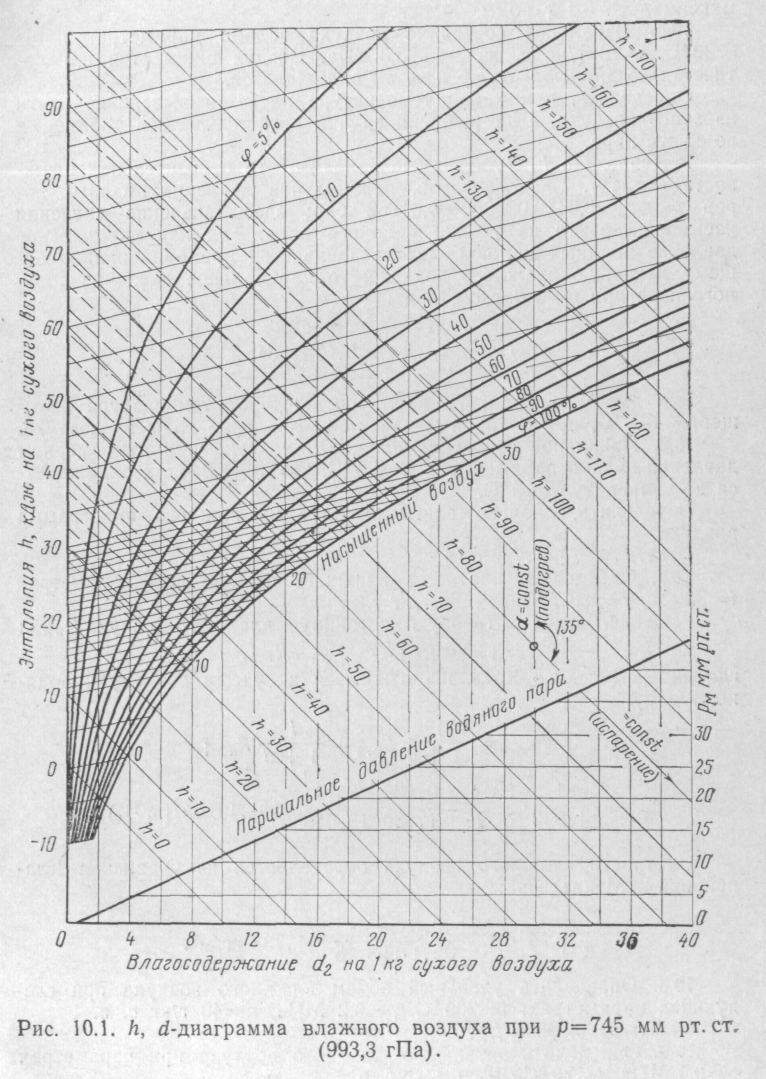
t_м = 16,5 °С - температура мокрого термометра;

t_р = 14 °С - температура точки росы;

φ = 73% - относительная влажность;

Р_п = 1,55 кПа или ≈ 12 мм. рт. ст. - парциальное давление водяных паров в воздухе;

h = 45 кДж/кг - энтальпия влажного воздуха.

 

 

Задача № 5.

В сушильной установке производится подсушка топлива с помощью воздуха при атмосферном давлении. От начального со­стояния с температурой t=22°С и относительной влажностью φ₁=50% воздух предварительно подогревается до температуры 70 °С и далее направляется в сушильную камеру, где в процессе высу­шивания топлива воздух охлаждается до 30 °С.

Рассчитать необходимое количество теплоты qдля нагревания 1 кг воздуха, параметры воздуха на выходе из сушильной камеры и количество воды, которое отбирает каждый килограмм воздуха от топлива. Считать, что тепловые потери отсутствуют. Определить также, какое максимальное количество воды мог бы унести с собой 1 кг воздуха, если бы он направлялся в сушильную камеру без предварительного подогрева.

 

Дано: t1 = 22 °С φ1 = 50% t2 = 70 °С t3 = 30 °С

 

Найти: q кДж/кг с. в.;

m г/кг с. в.;

m_{б. п.} г/кг с. в.;

φ %;

d г/кг с. в.

h кДж/кг с. в.

 

Решение:

Находим начальное состояние воздуха по h,d -диаграмме на пересечении изотермы t₁ = 22 °С с φ₁ = 50% (точка 1), для которой d₁ = 8 г/кг с. в., h₁= 43 кДж/кг.

Состояние воздуха после подогрева определится точкой 2 на пересечении d₁ = const и t₂ = 70 °С. Из этой точки проводим линию h₁= const до пересечения с t₃ = 30°С, где определяем точку 3, характеризующую состояние воздуха после сушильной камеры. Для этой точки d₃ = 24 г/кг с. в., h ₃ = h₂ = 92 кДж/кг с. в.; φ ₃ = 90 %.

Таким образом, на один килограмм сухого воздуха испаряется влаги

∆ d = d₃ – d₁ = 24 – 8 = 16 г/кг; а расход теплоты в калорифере на один килограмм сухого воздуха q = h ₂ – h₁= 92 – 43 = 49 кДж/кг.

Без подогрева процесс идет по 1 – 4, влагосодержание воздуха после сушильной камеры без прохождения им предварительного подогрева d₄ = 11 г/кг.

 

Тогда на один килограмм сухого воздуха испарится ∆ d = d₄ – d₁ = 11 – 8 = 3 г. воды.

 

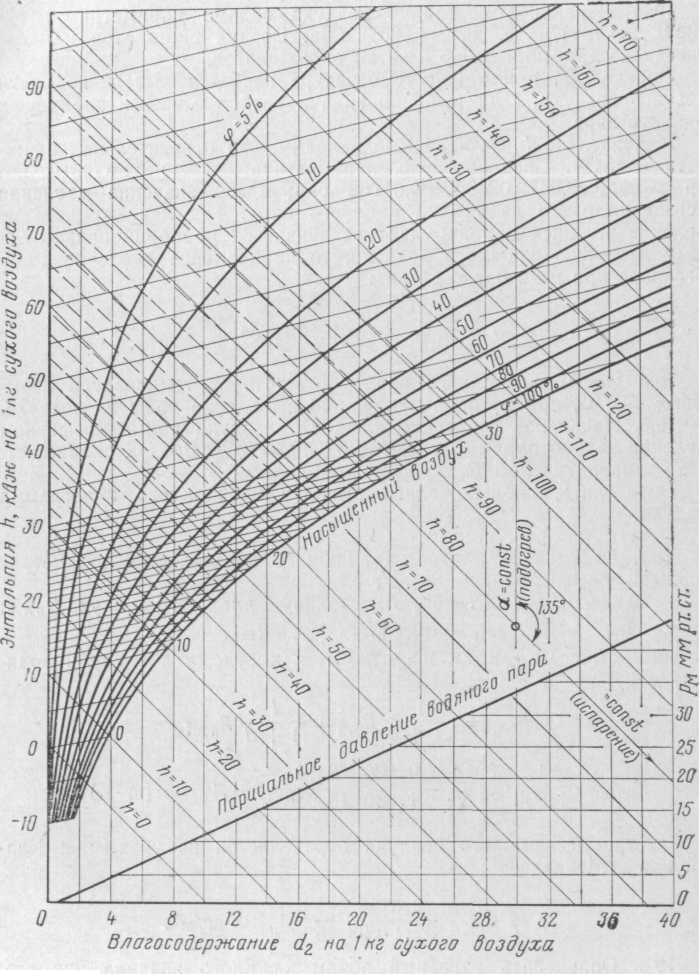
Ответ: q = 49 кДж/кг с. в.. С каждым килограммом сухого воздуха уходит 16,0 г. воды. На выходе из сушильной камеры параметры воздуха следующие: d = 24 г/кг с. в., φ = 90 %, h = 92 кДж/кг с. в.; если бы воздух не нагревался, то при прохождении через сушильную камеру каждый килограмм воздуха мог бы воспринять максимально 3 г. воды.

 

 

Раздел 2. Тепломассообмен.

 

Задача № 6.

 

Воздух при давлении р₁= 16 бар и при температуре t₁ =300°С движется в трубе внутренним диаметром d= 24 мм в количестве V_н = 80 м³ н/мин. При температуре t₁ кинематическая вязкость, теплопроводность и температуропроводность воздуха составляет v= 48,3∙10^-6 м²/с, λ= 4,6∙10^-2 Вт/(м∙К), а= 71,6∙10^-6 м²/с. Свнутренней стенки металлическая трубка покрыта накипью толщиной δ_н= 2 мм и теплопроводностью λ_н= 0,7 Вт/(м∙К). Толщина стенки металлической трубки δм= 20 мм, коэффициент её теплопроводности λ_м= 40 Вт/(м∙К). С наружной стороны трубка покрыта сажей толщиной δ_с= 1,5 мм и теплопроводностью λ_с= 0,1 Вт/(м∙К). Теплота передается в окружающий газ с температурой t₂= 20° С. Коэффициент теплоотдачи от поверхности сажи к окружающему газу а₂= 10 Вт/(м∙К). Стенку считать плоской.

Определить плотность теплового потока q через трехслойную стенку, температуру на поверхностях стенки t_ст1 и t_ст2, а также температуру слоев t_сл1, t_сл2.

 

Решение:

Дано: р₁= 16 бар Найти: q -?

t₁ =300°С t_ст1 -?

d = 24 мм t_ст2 -?

V_н = 80 м³ н/мин t_сл1 -?

v = 48,3∙10^-6 м²/с t_сл2 -?

λ = 4,6∙10^-2 Вт/(м∙К)

а = 71,6∙10^-6 м²/с

δ_н = 2 мм

λ_н = 0,7 Вт/(м∙К)

δ_м = 20 мм

λ_м = 40 Вт/(м∙К)

δ_м = 1,5 мм

λ_м = 0,1 Вт/(м∙К)

t₂ = 20° С

а₂ = 10 Вт/(м∙К)

1. Плотность азота найдем по формуле

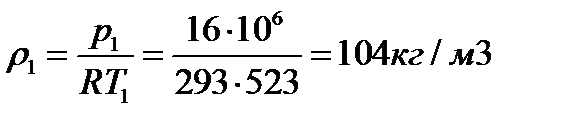, где R = 8314 /μ = 8314/ 28 = 293 Дж/кг∙К

 

2. Скорость определяем по формуле

m = ρ₁w₁F => w₁ = m / ρ₁F, где F – площадь трубки F = πd²/ 4, m = ρ_н V_{н ,}

где ρ_н для азота: ρ_н = μ/ 22,4 = 28 / 22,4 = 1,25 кг/м³

w₁ = m/ρ₁F = (1,25∙80)/(60∙104∙0,785∙0,024²) = 35,5 м/с

 

3. Число Рейнольдса

 

Re = wd / v = (35,5∙0,024∙10⁶) / 48,3 = 17639 > Re_{критич.} = 2300

 

4. Число Прандтля

 

Pr = v / а = 48,3 / 71,6 = 0,67

 

5. Критерий Нуссельта

 

Nu = 0,021 Re ^0,8 Pr ^0,43 = 0,021∙17639^0,8 ∙ 0,67^0,43 = 44

 

6. Коэффициент теплоотдачи

 

α₁ = Nu(λ/d) = 44(4,6 / 0,024) = 8433 Вт /(м² ∙K)

7. Коэффициент теплопередачи:

 

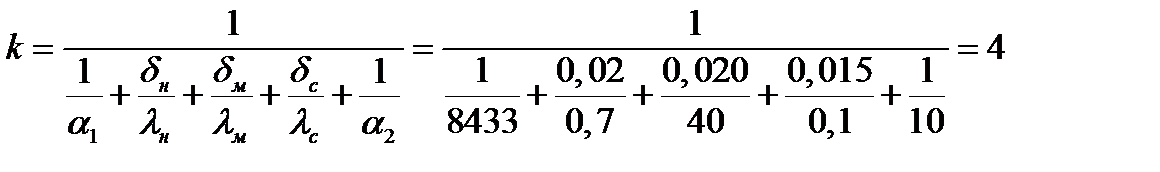Вт /(м² ∙K)

 

k = 4 Вт/(м² ∙K) < α₁ = 10 Вт /(м² ∙K)

 

8. Тепловой поток

 

q = k (t₁ – t₂) = 4(300 – 20) = 1120 Вт/м²

 

9. Из формулы

 

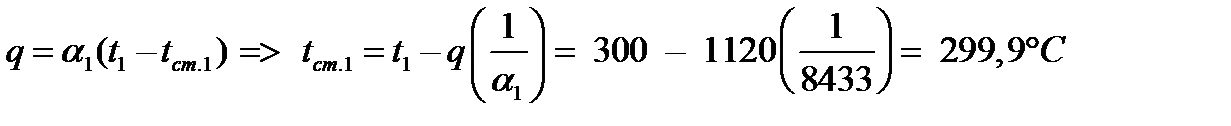
10.

 

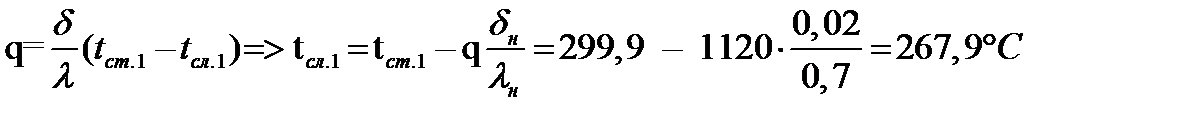
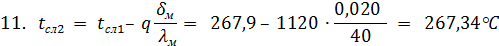
12. Из формулы q = 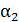(t_ст.2 – t₂) => t_ст.2 = t₂ + q 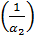= 20 + 1120 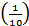= 132 °С

 

Ответ: q = 1120 Вт/м²; t_ст.1 = 299,9 °С; t_ст.2 = 132 °С; t_сл.1 = 267,9 °С;

t_сл.2 = 267,34 °С.

 

 

 

Задача № 7.

Вода при температуре насыщения t₁ =150° С движется в стальной трубке внутренним диаметром d= 30 мм. Расход воды составляет 0,15 м³/мин. При температуре t₁ кинематическая вязкость, теплопроводность и температуро-проводность воды составляет v= 6,89∙10^-6 м²/с, λ= 2,79∙10^{- 2} Вт/(м∙К), а= 6,13∙10^-6 м/с. С внутренней стенки металлическая трубка покрыта накипью толщиной δн= 2,3 мм и теплопроводностью λ_н= 0,75 Вт/(м∙К). Толщина стенки металлической трубки δ_м= 15 мм, коэффициент её теплопроводности λм= 50 Вт/(м∙К). С наружной стороны трубка покрыта сажей толщиной δ_с= 1,4 мм и теплопроводностью λ_с= 0,15 Вт/(м∙К). Теплота передается в окружающий газ с температурой t₂= 20° С. Коэффициент теплоотдачи от поверхности сажи к окружающему газу a₂= 10 Вт/(м²∙К). Стенку считать плоской.

Определить плотность теплового потока q через трехслойную стенку, температуру на поверхностях стенки t_ст1 и t_ст2, а также температуру слоев t_сл1, t_сл2.

 

Решение:

Дано:Найти:

t₁ =150°С t_ст1 -?

d = 30 мм t_ст2 -?

V_ж = 2,15 м³ н/мин t_сл1 -?

v = 6,89∙10^-6 м²/с t_сл2 -?

λ = 2,75∙10^-2 Вт/(м∙К) q -?

а = 6,13∙10^-6 м²/с

δ_н = 2,3 мм

λ_н = 0,75 Вт/(м∙К)

δ_м = 15 мм

λ_м = 50 Вт/(м∙К)

δ_с = 1,4 мм

λ_с = 0,15 Вт/(м∙К)

t₂ = 20° С

а₂ = 10 Вт/(м∙К)

1. Плотность воды составляет

ρ₁ = 1000 кг/м³

 

2. Скорость определяем по формуле

m = ρ₁w₁F = > w₁ = m / ρ₁ F, где F – площадь трубки F = πd² / 4, а m = ρ_н V_ж

где ρ_н для воды: ρ_н = μ/ 22,4 = 18 / 22,4 = 0,8 кг/м³

w₁ = (0,8∙2,15) / (60∙1000∙0,785∙0,030²) = 0,040 м/с

 

3. Число Рейнольдса

 

Re = wd / v = (0,040∙0,030∙10⁶) / 6,89 = 174

 

4. Число Прандтля

 

Pr = v / а = 6,89 / 6,13 = 1,12

 

5. Критерий Нуссельта

 

Nu = 0,021 Re^0,8 Pr^0,43 = 0,021∙174^0,8 ∙ 1,12^0,43 = 1,37

 

6. Коэффициент теплоотдачи

 

α₁ = Nu(λ/d) = 1,37(2,75 / 0,030) = 125 Вт /(м² K)

 

7. Коэффициент теплопередачи

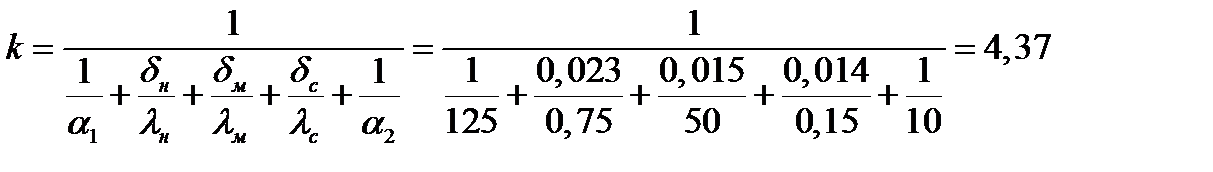Вт/(м² K)

 

k = 4,37 Вт/(м² ∙K) < α₁ = 10 Вт /(м² ∙ K)

 

8. Тепловой поток

 

q = k (t₁ – t₂) = 4,37(150 – 20) = 568,1 Вт/м²

 

9. Из формулы

 

q = α₁ (t₁ – t_ст.1) => t_ст.1 = t₁– q∙(1/α₁) = 150 – 568,1(1/125) = 145,4 °С

 

 

 

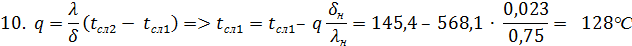
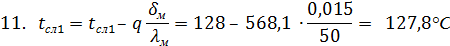
12. Из формулы q = α₂ (t_ст.2 – t₂) => t_ст.2 = t₂ + q∙(1/α₂) = 20 + 568,1 ∙ (1/10) = 37 °С

 

Ответ: q= 568,1 Вт/м²; t_ст.1 = 145,4 °С; t_ст.2 = 37 °С; t_сл.1 = 128 °С; t_сл.2 = 127,8 °С.

 

 

Задача № 8.

По трубе диаметром d = 35 мм протекает вода со ско­ростью w = 6 м/с. Температура внутренней поверхности трубы под­держивается t_c = 40 °С, и движущаяся по трубе вода нагревается от температуры на входе t_ж1 =14 °С до t_ж1 =22 °С.

Определить коэффициент теплоотдачи от стенки к воде и длину трубы.

 

Решение:

 

Определяем режим движения воды:

t_ж = 0,5 (t_ж1 + t_ж2) = 0,5(14+22) = 18 °С; при t_ж = 18 °С для воды ν_ж = 1,2∙10^-6 м²/с и

Rе_ж = (6∙35∙10^-3)/(1,2∙10^-6) =1,75∙10⁵ >10⁵

Режим турбулентный; для расчета коэффициента теплоотдачи используем формулу:

 

 

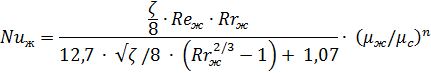
При t_ж = 18 °С Рr_ж = 7,0; μ_ж = 1004∙10^-6 Па∙с; λ _ж = 0,590 Вт/(м∙K);

ρ_ж = 998 кг/м³; с_рж = 4183 Дж/(кг∙K).

При t_c = 40 °С μ_с = 653∙10^-6 Па∙с.

ζ = (1,82 lg Rе_ж— 1,64)^-2 = [1,82 1g (1,75∙10⁵)—1,64]^-2 = 0,0160;

где при нагревании n =0,11; следовательно,

 

 

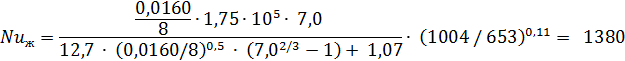
и коэффициент теплоотдачи

 

α = Nu _ж∙ (λ _ж / d) = 1380∙ (0,590 / 35∙10^-3 ) = 23263 Вт/(м² ∙K).

 

Длину трубы определяем из уравнения теплового баланса

 

Q = α(t_c— t_ж)πdl = G c_{р ж} (t_ж2 — t_ж1)

 

Расход воды и количество тепла, воспринимаемое водой,

G = ρ_ж∙ w (πd² / 4) = 998∙6∙(3,14∙ (35∙10^-3)² / 4)= 6,0 кг/с.

 

Q = G c_{р ж} (t_ж2 — t_ж1) = 6,0 ∙ 4183 ∙ 8 = 201 кВт.

 

Тогда

l = Q / (α(t_c— t_ж)πd) = 2,01∙10⁵ / (2,32∙10⁴ ∙(40 — 18) ∙3,14∙35∙10^-3) = 3,58 м.

 

Ответ: α =23263 Вт/(м²∙K); l = 3,58 м.

Задача № 9.

Паропровод наружным диаметром d =150 мм расположен в большом помещении с температурой воздуха t_ж =29 °С. Темпера­тура поверхности паропровода t_c1 = 390 °С. Определить тепловые потери с единицы длины паропровода за счет излучения и кон­векции.

Степень черноты поверхности паропровода ε = 0,8. Температуру стен помещения можно принять равной температуре воздуха, т. е. t_c2 = 28 °С.

Найти также соответствующие величины потерь при температуре паропровода 190 °С.

 

Решение:

Тепловые потери излучением

 

q_l^изл. = εС₀πd [(T_c1 / 100)⁴ — (T_c2 / 100)⁴]

 

При t_c1 = 390 °С

 

q_l^изл. = 0,8∙5,67∙3,14∙0,15 (6,73⁴ — 3,03⁴) = 5,5∙10³ Вт/м.

 

При t_c1 = 190 °С

 

q_l^{изл .} = 2,85(4,73⁴ — 3,03⁴) = 1,185∙10³ Вт/м.

 

Для определения коэффициента теплоотдачи конвекцией восполь­зуемся формулой Nu_ж = 0,50 (GrPr) _ж^1/4 для случая горизонтальной трубы.

 

В первом случае

 

 

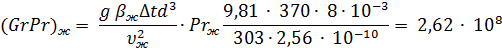
Во втором случае

 

(GrPr) _ж = 2,62∙ 10⁸(120 /360) = 0,9∙ 10⁸

 

Числа Нуссельта и коэффициенты теплоотдачи

Nu_ж = 0,50(2,62∙ 10⁸) ^1/4 = 63,5

Nu_ж2 = 0,50(0,9∙ 10⁸) ^1/4 = 49

α₁ = Nu_ж1 (λ_ж / d) = 63,5(2,59 ∙ 10^-2 / 1,15) = 10,9 Вт /(м²∙K)

α₂ = 8,46 Вт /(м²∙K)

 

Тепловые потери конвекцией: при t_c1 = 390 °С

q_l^конв. = α₁π (t_c—t_ж) = 10,9∙3,14∙0,15∙360 = 1848 Вт/м;

при t_c1 = 190 °С

q_l^конв. = 8,46∙3,14∙0,15∙120 = 478 Вт/м;

 

Ответ:

При t_c1 = 390 °С q_l^изл. = 5500 Вт/м q_l^конв. = 1848 Вт/м q_l^изл. / q_l^конв. = 2,98;

При t_c1 = 190 °С q_l^изл. = 1185 Вт/м q_l^конв. = 978 Вт/м q_l^изл. / q_l^конв. = 2,4.

Задача № 10.

Определить площадь поверхности нагрева и длину отдель­ных секций (змеевиков) змеевикового экономайзера парового котла, предназначенного для подогрева питательной воды в количестве

G₂ =240 т/ч от t'_ж2 =200 °С до t"_ж2 = 340 °С (см. рис.).

Вода движется снизу вверх по стальным трубам [λ_с = 22Вт/(м∙K)] диаметром

d₁/ d₂ =45/53 мм со средней скоростью ω = 0, 7м/с.

Дымовые газы (15% С0₂, 12% Н₂О) движутся сверху вниз в межтрубном пространстве со средней скоростью в узком сечении трубного пучка w₁ = 15 м/с. Расход газов G₁ = 510 т/ч. Температура газов на входе в экономайзер t'_ж1 = 750 °С. Трубы расположены в шахматном порядке с шагом поперек потока газов s₁ = 2,2 d и вдоль потока s₂ = 2,1 d.

 

Решение:

Среднеарифметическая температура воды

t_ж2 = 0,5 (t'_ж2 + t"_ж2) = 0,5 (200 +340) = 270 °С

 

При этой температуре физические свойства воды равны соот­ветственно:

ρ_ж2 = 767,9 кг/м³; с_{р ж2} = 5,07 кДж/(кг∙K); λ_ж2 = 0,590 Вт/(м∙K);

_ж2 = 0,133∙ 10^–6 м²/с; Рr_ж2 = 0,88.

 

Количество передаваемой теплоты:

Q = G ₂ с_рж2 (t"_ж2 – t'_ж2) = ((270∙10³) / 3600) ∙ 4,68 ∙ (340–200) = 4,0∙10⁴ кВт.

 

Число Рейнольдса для потока воды

Rе _ж2 = (w₂ ∙ d₁) / υ_ж2 = (0,7 ∙ 4,5 ∙ 10^–2) / (0,133 ∙ 10^–6) = 2,3 ∙ 10⁵

Опреде­ляем число Нуссельта и коэффициент теплоотдачи для воды, учитывая, что коэффициент теп­лоотдачи со стороны воды намного больше коэффициента теплоот­дачи со стороны газов и, следовательно, температура стенки трубы близка к температуре воды, полагаем (Рr_ж2 /Рr_с2)^0,25 ≈ 1:

Nu_ж2 = 0,021 Rе_ж2^0,8Рr_ж2^0,43 = 0,021(2,3∙10⁵)^0,8 (0,88)^0,43 = 315;

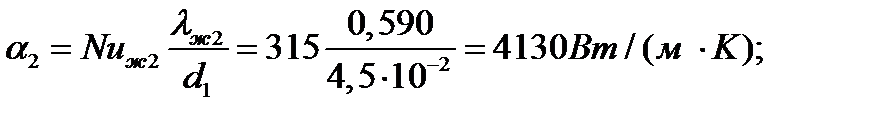
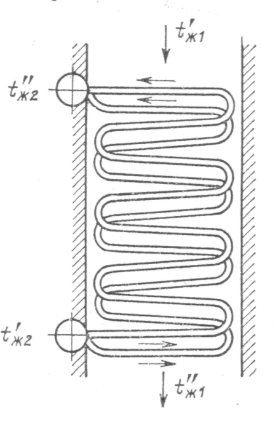Рис. 5. к задаче 15.

Для определения температуры газов на выходе из экономайзера примем в первом приближении теплоемкость газа с_рж1 ≈ 1,3 кДж /(кг ∙K).

Тогда:

 

t"_ж1 = t'_ж1 – (Q / (G ₁∙ с_рж1)) = 750 –((4,9∙10⁴) / (510 ∙10³∙1,3)) = 749,9 °С

и

t_ж1 = 0,5 (t'_ж1 + t"_ж1) = 0,5 (750 + 749,9) = 750 °С.

 

При этой температуре с_рж1 = 1,240 кДж/(кг∙K) и в результате второго приближения: t"_ж1 =750 °С и t_ж1 = 750 °С.

 

При температуре t_ж1 = 750 °С физические свойства дымовых га­зов данного состава равны соответственно:

 

Ρ_ж1 = 0,333 кг/м³; λ_ж1 = 0,0850 Вт/(м ∙K); _ж1 = 115∙ 10^–6 м²/с; Рr_ж1 = 0,61.

 

Число Рейнольдса для потока газов:

 

Rе _ж1 = (w₁ ∙ d₂) / _ж1 = (15 ∙ 5,3 ∙ 10^–2) / (115 ∙ 10^–6) = 6913

 

Найдем число Нуссельта и коэффициент теплоотдачи конвек­цией от газов к стенкам труб.

В связи с тем, что число рядов труб вдоль потока неизвестно, расчет ведем для третьего ряда труб. При шахматном расположе­нии для чистых труб по формуле:

 

Nu_ж1 =0,41 Rе_ж1^0,6Рr_ж1^0,33 ε_s = 0,41(6913)^0,6(0,61)^0,33 = 65,5.

 

где, так как s₁/s₂ =1,05, ε_s ≈ 1;

α'₁ = Nu_ж1 / (λ_ж1 ÷ d₂) = 65,5 / ((8,08 ∙ 10^–2) ÷ (5,3∙ 10^–2)) = 104 Вт/(м ∙K).

 

В промышленных условиях вследствие загрязнения котельных поверхностей нагрева интенсивность теплообмена снижается. Для учета этого полагаем:

 

α₁ = 0,8 α'₁ = 0,8∙104 = 83,2 Вт/(м ∙K).

 

Определяем коэффициент теплоотдачи излучением от потока га­зов к стенкам труб. Средняя длина пути луча:

 

l= 1,08 d ₂ ((s₁ ∙ s₂ ) / d₂²) – 0,785) = 1,08 ∙ 0,053 (2,2 ∙ 2,1– 0,785) = 0,219 м.

 

Произведение среднего пути луча на парциальное давление дву­окиси углерода и водяных паров:

 

р_СО2 ∙ l = 0,15 ∙ 0,219 = 0,0328 м ∙ кгс/см²;

р_Н2О ∙ l = 0,12 ∙ 0,219 = 0,0263 м ∙ кгс/см².

 

Находим степень черноты дымовых газов при средней температуре газов (t_{ж 1} = 750 °С):

 

ε_г = ε_СО2 + βε_Н2О = 0,078 + 1,08 ∙ 0,049 = 0,130.

 

Учитывая, что α₁ ‹‹ α₂, принимаем t_с1 ≈ t_ж2 + 20 ≈ 250 ⁰С. При этой температуре с помощью тех же графиков находим поглощательную способность газов при температуре поверхности труб:

 

А_г = ε_СО2 (Тж₁ / Тс₁)^0,65 + βε_Н2О = 0,064((750 + 273) / (250 + 273))^0,65 + 1,08 ∙ 0,07 = 0,18

 

Эффективная степень черноты оболочки:

 

ε'_с1 =0,5 (ε_с1 + 1) = 0,5 (0,8 + 1) = 0,9

 

Плотность теплового потока, обусловленная излучением,

 

q _л = ε'_с1 ∙ С₀ [ε_г (Т_ж1 /100)⁴ – А_г (Т_с1 /100)⁴] =

= 0,9 ∙5,7∙ [0,130 ∙ ((750+273)/100)⁴ – 0,18 ∙ ((250 + 273) /100)⁴] = 6613 Вт /м².

 

Коэффициент теплоотдачи, обусловленный излучением,

 

α_л =q_л / (t_ж1 – t_с1) = 6613 / (750 – 250) = 13,2 Вт/(м² ∙K).

 

Суммарный коэффициент теплоотдачи от дымовых газов к стен­кам труб:

 

α₀ = α₁ + α_л = 83,2 + 13,2 = 96,4 Вт/(м² ∙K).

 

Коэффициент теплопередачи

 

k = 1/((1/ α₀) + (δ_с/λ_с) + (1/ α₂)) =1/((1/ 96,4)+ (3,5∙ 10^–3 /22) + (1/ 4130)) = 59 Вт/(м² ∙K)

 

Находим средний температурный напор, приближенно принимая схему движений теплоносителей за противоточную:

 

(t'_ж1 – t"_ж2) / (t"_ж1 – t'_ж2) = (750 – 340) /(750 – 200) = 1,44 < 1,5

 

При этом

 

∆t_л ≈ ∆t_a = t_ж1 – t_ж2 = 750 — 270 = 480 °С.

 

Площадь поверхности нагрева экономайзера

 

F = Q / (k∆t_л) =((4,9 ∙ 10⁴) / (59 ∙ 480)) ∙ 10³ = 1730 м²

 

Число параллельно включенных змеевиков:

 

n = 4 G₂ / (ρ_ж2πd₁² w₂ 3600) = (4∙240 ∙10³) / (767,9 ∙3,14(4,5 ∙10^–2)² ∙ 0,7∙3600) = 78

 

Длина отдельной секции (змеевика)

 

l ₁ = F / (πd₂ n) = 1730 / (3,14 ∙ 5,3 ∙10^–2∙ 78) = 133 м.

 

Ответ: Площадь поверхности нагрева F = 1730 м²; число змеевиков n = 86;

длина змеевиков l ₁ = 133 м.

 

Задача № 11.

Вода с температурой t_ж1 = 25 °С поступает в трубу диаметром d = 10 мм и длиной l =2,0 м.

Определить температуру воды на выходе из трубы, если изве­стно, что расход воды G = 0,080 кг/с и температура внутренней по­верхности трубы t_c = 50 °С.

 

Решение:

 

Для расчета теплоотдачи необходимо знать среднюю по длине трубы температуру жидкости. Так как температура воды на выходе из трубы неизвестна, то задачу решаем методом последовательных приближений.

Задаемся температурой воды на выходе из трубы t_ж2 =35 °С.

Тогда t_ж =0,5 (t_ж