Раздел 3. Теплообменные аппараты.

 

Задача № 12.

 

По трубам вертикального теплообменника снизу вверх течет вода. Внутренний диаметр труб d =14 мм; их длина l= 1,1 м. Расход воды через одну трубу G = 56 кг/ч. Температура воды на входе в теплообменник t_ж1 = 40 °С.

Определить количество тепла, передаваемого от стенки одной трубы к воде, и температуру воды на выходе, если температура стенок труб поддерживается равной 70 °С.

 

Решение:

 

Секундный расход воды: G = 56/3600 = 1,55∙10^-2 кг/с

 

При t_ж1 = 40 °С вязкость μ_ж1 = 653∙10^-6 Па∙с

 

и Re_ж1 = 4 G / (πd μ_ж1) = (4 ∙ 1,55 ∙ 10^-2) / (3,14∙14∙10^-3∙653∙10^-6) = 2159 < 2300.

 

Режим течения ламинарный.

 

Далее необходимо вычислить произведение (GrPr)_г. Так как нам неизвестно значение температуры воды на выходе, t_ж2 и, следовательно, нельзя найти её среднюю температуру, t_ж, то задачу решаем методом последовательных приближений.

 

Задаемся t_ж2 = 60 °С.

 

Тогда

 

t_ж = 0,5 (t_ж1+ t_ж2) = 0,5(40+60) =50 °С и t_г = 0,5 (t_с+ t_ж) = 0,5(70+50) = 60 °С.

 

При этой температуре

 

β_г = 5,11 ∙ 10^-4 К^-1; ν_г = 0,478 ∙ 10^-6 м²/с; Рr_г = 2,98;

 

 

 

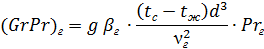
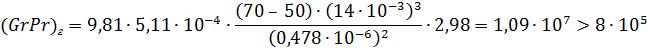
Режим течения вязкостно-гравитационный.

При вязкостно-гравитационном режиме течения в вертикальных трубах и совпадении направлений вынужденной и свободной кон­векции у стенки (охлаждение жидкости и течение сверху вниз или нагревание и течение снизу вверх) для расчета средней теплоотдачи можно воспользоваться следующей формулой:

 

Nu_c = 0,35 (Pe_г(d/l)^0,3) [(GrPr) _г∙(d/l)]^0,18

где коэффициент теплоотдачи отнесен к начальной разности темпе­ратур t_с - t_ж;

 

Индексы «с » и «г » означают, что соответствующие физические свойства выбираются по температуре стенки t_с и t_г= 0,5 (t_с + t_ж ).

 

Формула Nu_c = 0,35 (Pe_г(d/l)^0,3) [(GrPr)_г∙(d/l)]^0,18 справедлива при Re_ж < 2300;

(Pe_г(d/l))_ас ≤ Pe_г(d/l) ≤ 110; 20 ≤ l/d ≤ 130; 8∙10⁵ ≤ (GrPr)_г ≤ 4∙10⁸

 

Здесь асимптотическое значение числа Пекле:

 

(Pe_г (d/l)) _ас ≈ 1,5(GrPr (d/l)) _г^0,25

В рассматриваемом случае:

при t_г = 60 °С; а_г= 1,6∙10^-7 м²/с; при t_с = 70 °С; λ_с = 0,668 Вт/(м∙K);

при t_ж = 50 °С ρ_ж = 988 кг/м³.

 

Средняя скорость течения воды

 

w = 4 G / (πd² ρ_ж) = 4 ∙ 1,55∙ 10^-2 / (3,14 ∙(14∙ 10^-2)² ∙ 988) = 0,101 м/с

 

 

 

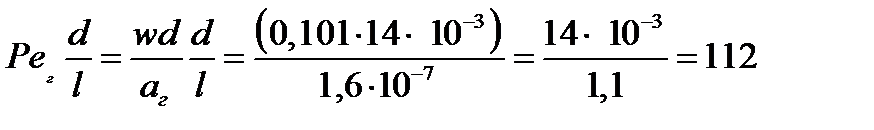
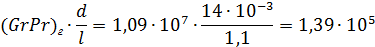
(Pe_г(d/l))_ас ≈ 1,5(1,39∙10⁵)^0,25 = 29,17

 

Так как все критерии находятся в указанных выше пределах, то формула Nu_c = 0,35(Pe_г(d/l)^0,3) [(GrPr) _г∙(d/l)]^0,18 применима.

Nu_c = 0,35(112)^0,3(1,39∙10⁵)^0,18 = 12,15.

 

Коэффициент теплоотдачи

 

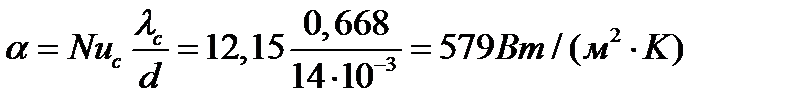
Количество передаваемого тепла

 

Q = α (t_с—t_ж)πdl = 579(70—50) π 14∙10^-3 ∙ 1,1 = 559 Вт.

 

Проверка принятого значения температуры воды на выходе из трубы:

 

t_ж2 = t_ж1 + (Q/Gc_pж) = 40 +(559/(1,55∙10^-2 ∙4174)) = 40 + 8,64 = 48,64 °С

где теплоемкость воды выбрана при t_ж = 50 °С; с_рж = 4174 Дж/(кгK).

 

Таким образом, в результате первого приближения t_ж2 = 48,64 °С.

 

Задавшись для второго приближения t_ж2 = 50 °С, получим t_ж = 0,5 (t_ж1 + t_ж2) =45 °С и t_г =0,5 (t_с+ t_ж)= 57,5 °С. Совпадение достаточно хорошее и дальнейших пересчетов делать не нужно.

 

Ответ: Q = 559 Вт; t_ж2 ≈ 49 °С.

 

 

Задача № 13.

По трубе внутренним диаметром d = 44 мм движется воз­дух с высокой скоростью. Расход воздуха G = 0,25 кг/с.

Термодинамическая температура воздуха на входе в трубу t₁ =1100 °С. Температура стенки трубы t_c = 300 °С. Давление воздуха на входе p₁ = 700 мм рт. ст. и на выходе р₂ = 500 мм рт. ст.

Какой длины должна быть труба, для того чтобы термодина­мическая температура на выходе t₂ равнялась 700 °С Определить также значения числа Маха на входе в трубу и на выходе из нее.

 

Решение:

Давление воздуха на входе и выходе из трубы

p₁ = 700∙13,6∙9,81 = 93391 Па;

р₂ = 500∙13,6∙9,81 = 66708 Па.

 

Плотность воздуха на входе в трубу

ρ₁ = p₁ / RT₁ = 93391 / 287,4(1100 + 273) = 0,237 кг/м³

на выходе

ρ₂ = p₂ / RT₂ = 66708 / 287,4(700 + 273) = 0,238 кг/м³

где для воздуха R = 287,4 Дж/(кг∙K).

Скорость воздуха на входе

 

 

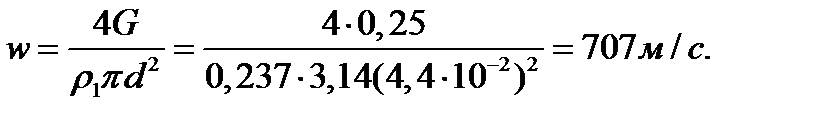
на выходе

 

w₂ = w₁∙ (ρ₁ / ρ₂) = 707 ∙ (0,237/0,238) = 704 м/с.

Скорость звука и значения числа Маха:

 

α₁ = √kRT₁ = 20,1 √T₁ = 20,1 √ 1373 = 745 м/с.

M₁= w₁/ α₁ = 707 / 745 = 0,95;

α₂ = 20,1 √T₂ = 20,1 √ 973 = 627 м/с.

M₂= w₂/ α₂ = 704 / 627 = 1,12;

 

Температура торможения

 

υ₁= T₁ + (w₁² / 2 c_p1) = 1373 + (707² / 2∙1197) = 1373 + 209 = 1582 K,

 

где при t₁ =1100 °С с _p1 =1,197 кДж/(кг∙K)

 

υ₂= T₂ + (w₂² / 2 c_p2) = 973 + (704² / 2∙1135) = 973 + 218 = 1191 K,

 

где при t₂ =700 °С с_р2=1,135 кДж/(кг∙K).

 

Среднелогарифмическая разность температур торможения

 

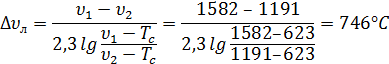
Среднеарифметическая температура воздуха

 

Т =0,5 (Т₁ + Т₂) = 0,5 (1373+973) = 1173 К

или t = 1173—273 = 900 °С.

 

Коэффициент теплоотдачи в рассматриваемых условиях может быть приближенно рассчитан по формуле Nu = Nu_ж (1,27– 0,27Θ), где в качестве определяющей температуры принимается t, а коэффициент теплоот­дачи отнесен к разности температур Δυ_л. При t=900 °С λ_ж = 7,63∙10^-2 Вт/(м∙K); μ_ж = 46,7∙10^-6 Па∙с; c _{p ж} =1,172 кДж/(кг∙K); Рr_ж = 0,717.

Re _ж = 4 G / (πd μ_ж) = (4∙0,25) / (3,14∙4,4∙10^-2∙46,7∙10^-6) = 1,5 ∙ 10⁵

 

Предполагая, что отношение l / d > 50, найдем:

Nu _ж = 0,021 Re^0,8_жPr^0,43_ж = 0,021∙(1,5∙10⁵)^0,8∙(0,717)^0,43 = 251.

 

Поправка на температурный фактор по нижеследующей формуле при охлаждении газа:

Nu = Nu_ж (1,27— 0,27Θ), где Θ = T_c / T = 623 / 1173 = 0,5

 

Таким образом,

Nu = 251 (1,27— 0,27 ∙ 0,5) = 285;

α = Nu(λ_ж / d) = 285(7,63∙10^-2 / 4,4∙10^-2) = 494 Вт/(м² ∙K);

 

Плотность теплового потока

q = α Δ 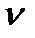_л = 494 ∙ 746 = 3,68∙10⁵ Вт/м².

 

Количество передаваемого тепла

Q = G c_{p ж} (υ₁— υ ₂) = 0,25∙1172(1582—1191) = 1,14∙10⁵ Вт.

 

Поверхность теплообмена

F = Q / q = (1,14∙10⁵) / (3,68∙10⁵) = 0,309 м².

 

Искомая длина трубы

l = F / πd = 0,309 / (3,14 ∙ 4,4∙10^-2) = 2,2 м.

 

Ответ: l = 2,2 м; М₁ = 0,95; М₂ = 1,12.

 

Задача № 14.

Определить коэффициент теплоотдачи излучением от по­тока газа к поверхности труб пароперегревателя парового котла, если температура газа на входе t_г1 = 1050 °С и на выходе из паро­перегревателя t_г2 = 750 °С. Принять среднюю температуру всей по­верхности теплообмена постоянной и равной t_с =450 °С и степень черноты поверхности ε_с = 0,8. Трубы расположены вшахматном порядке (рис. 3) с шагами по фронту s₁ = 2 d и глубине s₂ = 2 d; внешний диаметр труб d = 36 мм. Газ содержит 11% С0₂ и 3% H₂О. Общее давление газа p = 98,0 кПа.

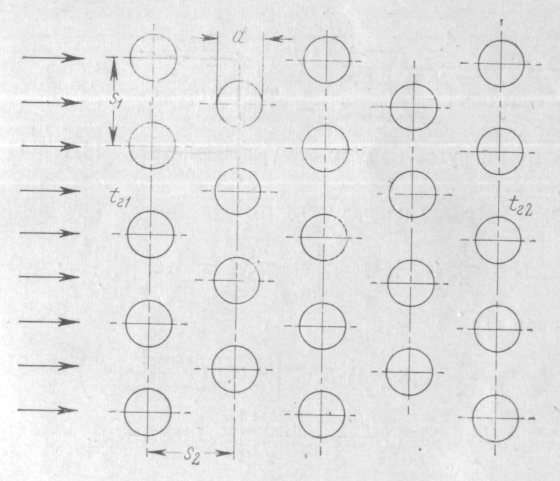Рис. 3. к задаче 13.

Решение:

 

Средняя длина пути луча в межтрубном пространстве определяется по формуле:

l = 1,08 d((s₁s₂ / d²) – 0,785) = 1,08∙0,036(2∙2–0,785) = 0,125 м.

 

Произведения парциального давления углекислого газа и водяных паров на среднюю длину пути луча равны:

Р_СО2 l = 0,11∙ 9,80∙ 10⁴∙ 0,125 = 0,135∙ 10⁴ м ∙Па

Р_Н2О l = 0,03 ∙ 9,80∙ 10⁴∙ 0,125 = 0,0367∙ 10⁴ м ∙Па

 

Средняя температура газов

t_г = 0,5 ∙ (t_г1 + t_г2) = 0,5(1050 + 750) = 900 °С.

 

При средней температуре газов по графикам находим степени черноты СО₂ и Н₂О:

ε _СО2 = 0,045;

ε_Н2О = 0,017.

 

По графику находим поправку β и вычисляем сте­пень черноты газов при средней температуре газов

ε _г = ε _СО2 + β ε_Н2О = 0,045 + 1,05 ∙ 0,017 = 0,063

 

Поглощательная способность газов при температуре поверхно­сти труб

А_г = ε _СО2 (Т_г / Т_с)^0,65 + β ε_Н2О = 0,045((900+273)/(450+273))^0,65 + 1,05∙0,032 = 0,0946,

где ε _СО2 и ε_Н2О берутся по тем же графикам при температуре стенки.

 

Тепловая нагрузка поверхности труб за счет излучения

q_л = 0,5(ε _с +1) С₀ [ ε _г (Т_г / 100)⁴ — А_г (Т_с /100)⁴ ]

 

В данном случае

q_л = 0,5(0,8+1)∙5,67[ 0,063(900+273 / 100)⁴ — 0,0946(450+273 /100)⁴ ] = 4767 Вт/м².

 

Коэффициент теплоотдачи излучением

α_л = q_л /(t_г— t_с) = 4767/(900— 450)=10,6 Вт/(м²∙K).

 

Ответ: α_л = 10,6 Вт/(м²∙K).

Задача № 15.

Определить поверхность нагрева и число секций водоводяного теплообменника типа «труба в трубе» (рис. 4). Грею­щая вода движется по внутренней стальной трубе [λ_с = 40 Вт/(м∙K)] диаметром d₂/d₁ = 34/31 мм и имеет температуру на входе t'_ж1 = 90 °С. Расход греющей воды G₁ = 2120 кг/ч.

Нагреваемая вода движется противотоком по кольцевому каналу между трубами и нагревается от t'_ж2 = 13 °С до t''_ж2 = 45 °С. Внут­ренний диаметр внешней трубы D =46 мм. Расход нагреваемой воды G₂ = 3100 кг/ч. Длина одной секции теплообменника l = 1,5 м.

Потерями тепла через внешнюю поверхность теплообменника пренебречь.

 

Решение:

Теплоемкость воды с_р =4,19 кДж/(кг ∙K).

 

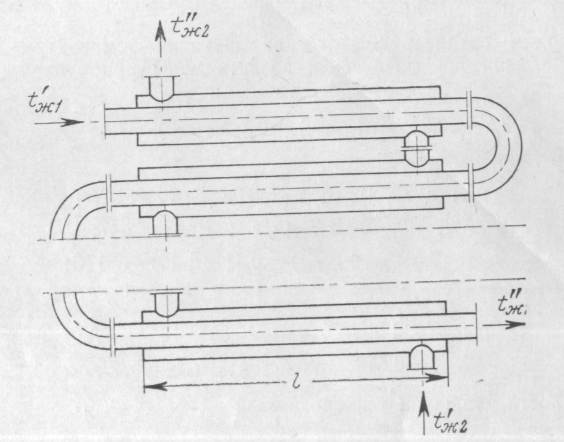Рис. 4. к задаче 14.

Количество передаваемого тепла

Q =G₂ с_р2(t''_ж2 — t'_ж2 ) = (3100/3600)∙4,19∙(42—13) = 105 кВт.

 

Температура греющей воды на выходе

t''_ж1= t'_ж1—(Q / G₁ с_р1) = 90—((105 ∙ 3600) / (2120 ∙ 4,19)) = 47 °С

 

Находим среднеарифметические значения температур теплоно­сителей и значения физических свойств воды при этих температу­рах:

t_ж1 = 0,5(t'_ж1+ t''_ж1) = 0,5 (90+47) =68,5 °С;

 

при этой температуре

 

ρ_ж1 = 977 кг/м³; 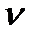_ж1 = 0,415∙10^-6 м²/с; λ _ж1 = 0,670 Вт/(м∙°С); Рr_ж1 = 2,55;

 

t_ж2 = 0,5(t'_ж2+ t''_ж2) = 0,5(13+42) =27,5 °С;

 

при этой температуре

 

ρ_ж2 = 995 кг/м ³; 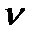_ж2 = 0,805∙10^-6 м²/с; λ _ж2 = 0,618 Вт/(м∙K); Рr_ж2 = 5,42.

 

Скорости движения теплоносителей

 

 

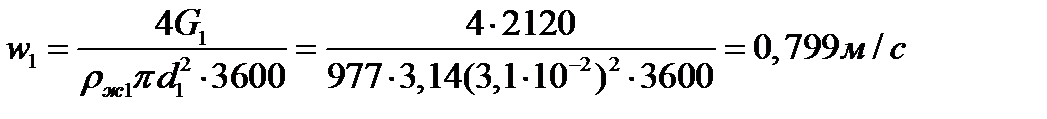
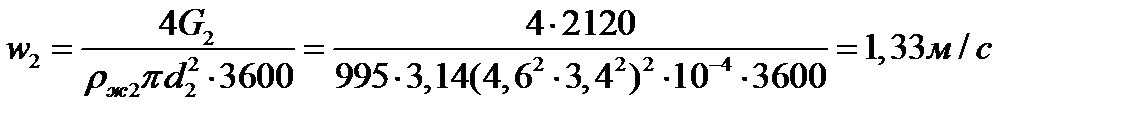
Число Рейнольдса для потока греющей воды

 

 

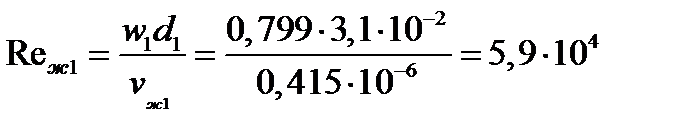
Режим течения греющей воды турбулентный и расчет числа Нуссельта и коэффициента теплоотдачи ведем по следующей формуле:

 

Число Нуссельта

 

Nu _ж1 = 0,021 Re^0,8_ж1 Pr^0,43_ж1(Pr_ж1/ Pr_с1)^0,25

Так как температура стенки неизвестна, то в первом приближе­нии задаемся значением

 

t_c1 ≈ 0,5(t_ж1+ t_ж2) = 0,5(68,5+27,5) =48 °С.

 

При этой температуре Рr_c1 = 3,5; тогда

 

Nu _ж1 = 0,021(5,9∙10⁴)^0,8 ∙ (2,55)^0,43 ∙(2,55/ 3,5)^0,25 = 189

 

Коэффициент теплоотдачи от греющей воды к стенке трубы

α₁ = Nu _ж1(λ _ж1/d₁) = 189(0,668 / 3,1∙10^-2) = 4073 Вт/(м²∙ K).

 

Число Рейнольдса для потока нагреваемой воды

Re _ж2 = (w₂d_э / 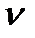_ж2) = (1,33∙1,2∙10^-2)/(0,805∙10^-6) = 1,98∙10⁴

 

где эквивалентный диаметр для кольцевого канала

d_э = D—d₂ = 46—34 = 12 мм.

 

Режим течения нагреваемой воды турбулентный и расчет числа Нуссельта и коэффициента теплоотдачи ведем по формуле для теплоотдачи при турбулентном течении в каналах кольцевого сечения:

Nu _ж2 = 0,017 Re^0,8_ж2 Pr^0,43_ж2(Pr_ж2/ Pr_с2)^0,25∙(D/d₂)^0,18

 

Приняв в первом приближении t_c2 ≈ t_c1 и, следовательно, Рr_c2 ≈ Рr_c1 ≈ 3,5, получим:

Nu _ж2 = 0,017(1,98∙10⁴)^0,8 ∙(5,42)^0,43∙(5,42/ 3,5)^0,25∙(46/34)^0,18 = 107

 

Коэффициент теплоотдачи от стенки трубы к нагреваемой воде

 

α₂ = Nu _ж2(λ _ж2/d_э) = 107(0,618 / 1,2∙10^-2) = 5510 Вт/(м²∙K).

 

Коэффициент теплопередачи

 

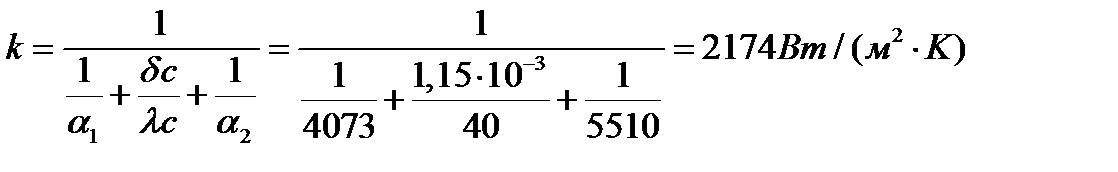
Так как в рассматриваемая случае 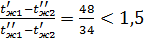то с достаточной точ-

ностью можно вести расчет по среднеарифметиче­ской разности температур:

Δ t_а = t_ж1− t_ж2 = 68,5− 27,5 = 41,0 °С.

Плотность теплового потока

q = k∙Δt_a = 2174 ∙ 41,0 = 8,91∙ 10⁴ Вт/м².

 

Поверхность нагрева

F = Q/q = 105/89,1 = 1,18 м²

Число секций

n = F / (πd₁l) = 1,18 / (3,14∙ 3,1∙ 10^-2 ∙ 1,5) = 8

 

Температура поверхностей стенок трубы

t_c1 = t_ж1 − (q/α₁) = 68,5 − (89100/4073) = 46,6 °С.

t_c2 = t_ж2 − (q/α₂) = 27,5 − (89100/5510) = 43,67 °С.

 

При этих температурах Рr_c1 = 3,82 и Рr_c2 = 4,02 и поправки на изменение физических свойств жидкости по сечению потока имеют следующие значения:

(Pr_ж1/ Pr_с1)^0,25 = (2,55 / 3,82)^0,25 = 0,904 (в расчете было принято 0,91);

(Pr_ж2/ Pr_с2)^0,25 = (5,42 / 4,02)^0,25 = 1,077 (в расчете было принято 1,1).

 

Совпадение достаточно точное; можно принять, что F =1,18 м² и n = 8.

Ответ: F =1,18 м²; n = 8.