ИНДИВУДУАЛЬНОЕ ЗАДАНИЕ №1
По заданию образец с исходной площадью поперечного сечения 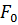 подвергается деформации. В первом случае испытание производится при атмосферном давлении
подвергается деформации. В первом случае испытание производится при атмосферном давлении 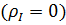 , в двух других - под воздействием всестороннего давления жидкости, соответственно,
, в двух других - под воздействием всестороннего давления жидкости, соответственно, 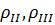 . Разрушение образцов происходит в момент, когда напряжение достигает заданной величины
. Разрушение образцов происходит в момент, когда напряжение достигает заданной величины 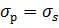 , при этом площадь поперечного сечения составляет, соответственно,
, при этом площадь поперечного сечения составляет, соответственно,  . Необходимо определить значения показателей напряженного состояния
. Необходимо определить значения показателей напряженного состояния 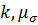 в момент разрушения и построить диаграмму пластичности
в момент разрушения и построить диаграмму пластичности 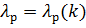 . Исходные данные представлены в таблице 4.
. Исходные данные представлены в таблице 4.
Таблица 4 – Исходные данные
| Вид деформации | 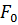 , мм2 , мм2
|  , мм2 , мм2
| 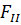 , мм2 , мм2
| 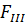 , мм2 , мм2
| 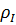 , МПа , МПа
| 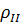 , МПа , МПа
| 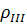 , МПа , МПа
| 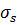 , МПа , МПа
|
| Растяжение |
Теоретическая часть
Пластичностью называют способность металла деформироваться при тех или иных значениях термомеханических параметров без разрушения в виде макроскопического нарушения сплошности [1-8].
Термомеханическими параметрами называют величины, определяющие термические и механические условия протекания пластической деформации. К числу таких параметров относят, в частности, температуру, составляющие тензоров напряжения и скорости деформации.
Мерой пластичности служит степень деформации сдвига, накопленная металлом к моменту разрушения ( ). Величина является индивидуальной для каждого материала.
). Величина является индивидуальной для каждого материала.
Предельная деформация сдвига определяется по формуле:
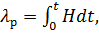 (1)
(1)
где 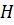 – интенсивность скорости деформации сдвига:
– интенсивность скорости деформации сдвига:
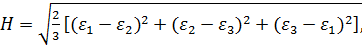 (2)
(2)
По закону сохранения объема, 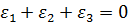 , причем
, причем 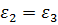 (растяжение одноосное).
(растяжение одноосное).
Таким образом, 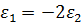 .
.
Истинная деформация определяется по формуле:
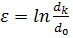 , (3)
, (3)
где  – первоначальный диаметр заготовки;
– первоначальный диаметр заготовки;
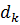 – диаметр заготовки после пластической деформации.
– диаметр заготовки после пластической деформации.
Из формул (1-3) следует, что предельная деформация сдвига в данном случае равна:
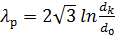 , (4)
, (4)
Остальные общеизвестные и широко применяемые на практике показатели пластичности, такие, как относительное удлинение и относительное сужение, можно пересчитать в показатель 
Кроме понятия «пластичность», в теории обработки металлов давлением (ОМД) используется понятие «деформируемость», т.е. способность тела в целом изменять свою форму без макроскопического разрушения.
Основными факторами, влияющими на пластичность металлов при обработке давлением, являются: состав и структура деформируемого металла; реализуемая схема напряженного состояния; неравномерность деформации; температура деформации; скорость деформации; степень деформации; режим термической обработки.
В общем случае под схемой напряженного состояния понимают графическое представление о наличии и знаке главных нормальных напряжений, составляющих тензор напряжения.
Показателями напряженного состояния называют составленные из инвариантов тензора напряжений безразмерные величины, от которых существенно зависит пластичность металлов.
Правило знаков: растягивающие напряжения считаются положительными, а сжимающие – отрицательными.
В теории ОМД обычно используют два основных показателя напряженного состояния: показатель формы девиатора напряжений или коэффициент Лоде (в данной работе не рассматривается) и показатель схемы напряженного состояния:
 , (5)
, (5)
где σ – среднее нормальное напряжение;
T – интенсивность касательных напряжений.
 (6)
(6)
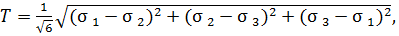 (7)
(7)
Установлено, что при обработке давлением не существует металлов и сплавов, обладающих неизменными пластическими свойствами, а есть хрупкое и пластичное состояния, определяемые условиями нагружения при деформировании. При этом, чем в большей степени выражены в схеме напряженного состояния сжимающие напряжения, тем выше пластичность обрабатываемого металла.
Наиболее благоприятной для проявления металлом пластических свойств является схема всестороннего неравномерного сжатия. Появление в схеме растягивающих напряжений снижает пластичность, и самой низкой пластичностью характеризуется схема всестороннего растяжения, которая в реальных процессах обработки давлением практически не встречается.
В нашем случае схема напряженного состояния представляет собой одноосное сжатие (рис. 1).
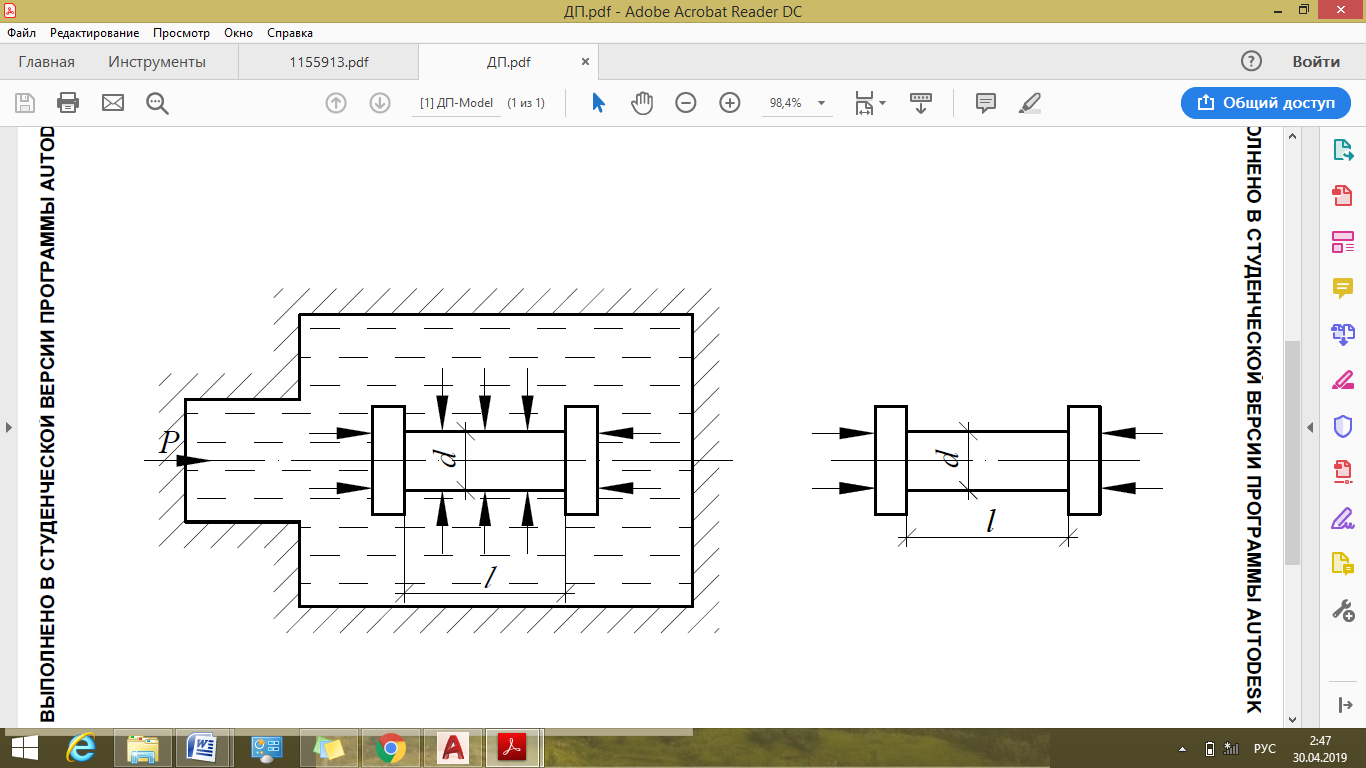
| 
|
| а | б |
Рисунок 1 – Схема испытания для определения пластических свойств металла: а - при атмосферном давлении; б - под воздействием всестороннего давления жидкости
Таким образом, уравнения для определения напряжений выглядят следующим образом:
1) при атмосферном давлении:
 (8)
(8)
2) при давлении жидкости 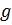 , в одинаковой мере изменяющей главные нормальные напряжения:
, в одинаковой мере изменяющей главные нормальные напряжения:
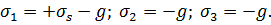 (9)
(9)
Решение
1. По формуле (4) определим предельную деформацию сдвига.
 Площадь круга определяется по формуле
Площадь круга определяется по формуле 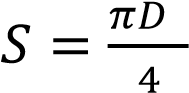 , откуда
, откуда 
а) 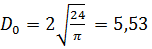 (мм);
(мм);
б)  (мм);
(мм);
в) 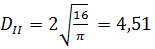 (мм);
(мм);
г) 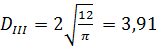 (мм);
(мм);
Таким образом, 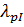 =2
=2 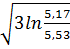 =0,066
=0,066
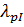 =2
=2 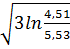 =0,3049
=0,3049
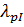 =2
=2 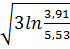 =4,899
=4,899
2. Используя формулы (5-7), определим коэффициент пластичности 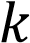 :
:
а) для испытания при атмосферном давлении:
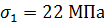 ;
; 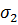 =0;
=0; 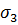 =0;
=0;
 (22+0+0)
(22+0+0)
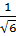
 =
=
б) для испытания при воздействии всестороннего давления жидкости 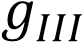 :
:
 =22 – 30 = -8 (МПа)
=22 – 30 = -8 (МПа) 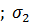 = - 30 (МПа)
= - 30 (МПа)  = - 30 (МПа);
= - 30 (МПа);
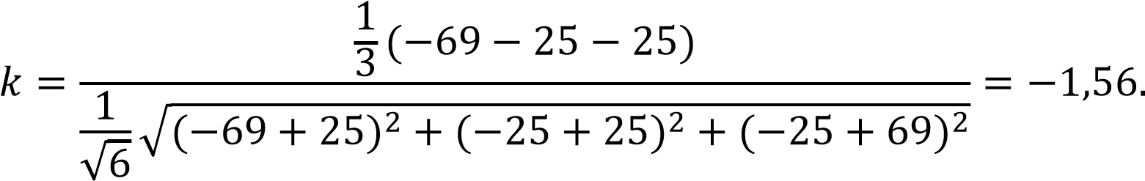
в) для испытания при воздействии всестороннего давления жидкости  :
:
 =-22 – 30 = -50 (МПа)
=-22 – 30 = -50 (МПа)  = - 30 (МПа)
= - 30 (МПа)  = - 50 (МПа);
= - 50 (МПа);

Полученные значения представим в виде таблицы 2.
Таблица 2 – Расчётные значения
| 
| |
| 0,65 | -0,58 | |
| 1,14 | -1,94 | |
| 1,52 | -7,17 |
Построим график, используя значения из таблицы 5, рисунок 1.
Рисунок 2 – Диаграмма пластичности 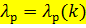
В случае сжатия график 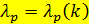 располагается во II четверти. Зависимость
располагается во II четверти. Зависимость 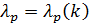 убывающая. Она показывает, что рост сжимающих напряжений всегда повышает пластичность металла при прочих равных условиях.
убывающая. Она показывает, что рост сжимающих напряжений всегда повышает пластичность металла при прочих равных условиях.