Необходимо:
1) построить в масштабе геометрию очага деформации при волочении широкой полосы через клиновую волоку;
2) построить в масштабе годографы скоростей 
мм/сек;
3) определить безразмерные напряжения волочения.
Таблица 9 – Исходные данные задания №3
 , мм
|  , мм
|  , град.
| 
|
| 0,30 |
Теоретическая часть
Рассматривается процесс волочения широкой полосы из неупрочняемого металла. Деформация осуществляется в условиях близких к плоскому деформированному состоянию.
Определим напряжение протягивания 
через коническую волоку с полууголом при вершине конуса .
Начальная толщина полосы - , конечная - . Скорость движения полосы на входе - 
, на выходе - 
.
Течение металла происходит так, как показано на рис.7.
Рисунок 7 – Схема течения металла в конической волоке
В полосе выделим три характерные области: I, II и III, в которых течение плоско-параллельное без деформации.
В очаге деформации строится простейшее кинематически возможное поле скоростей, называемое годографом скоростей.
Найдем скорость движения полосы на выходе:
(20)
Выбранное поле скоростей содержит неизвестную варьируемую величину 
. Угол можно определить вариационным методом, суть которого является в отыскании таких функций напряжений и деформаций, при которых энергия минимальна.
Таким образом, из всех кинематически возможных полей скоростей действительным будет то, при котором мощность силы волочения минимальна.
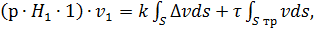(21)
где 
- характеристика материала, 
- скачок скорости на поверхности разрыва, 
- трение.
Трение на контакте полосы и волоки примем заданным по Зибелю:
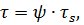(22)
где ψ – коэффициент трения.
(23)
С учетом вышесказанного функция примет вид:
(24)
;
;
.
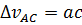Таким образом,
(25)
Решение
Рисунок 8 – Годограф скоростей (вариация №1)
Рисунок 9 – Годограф скоростей (вариация №2)
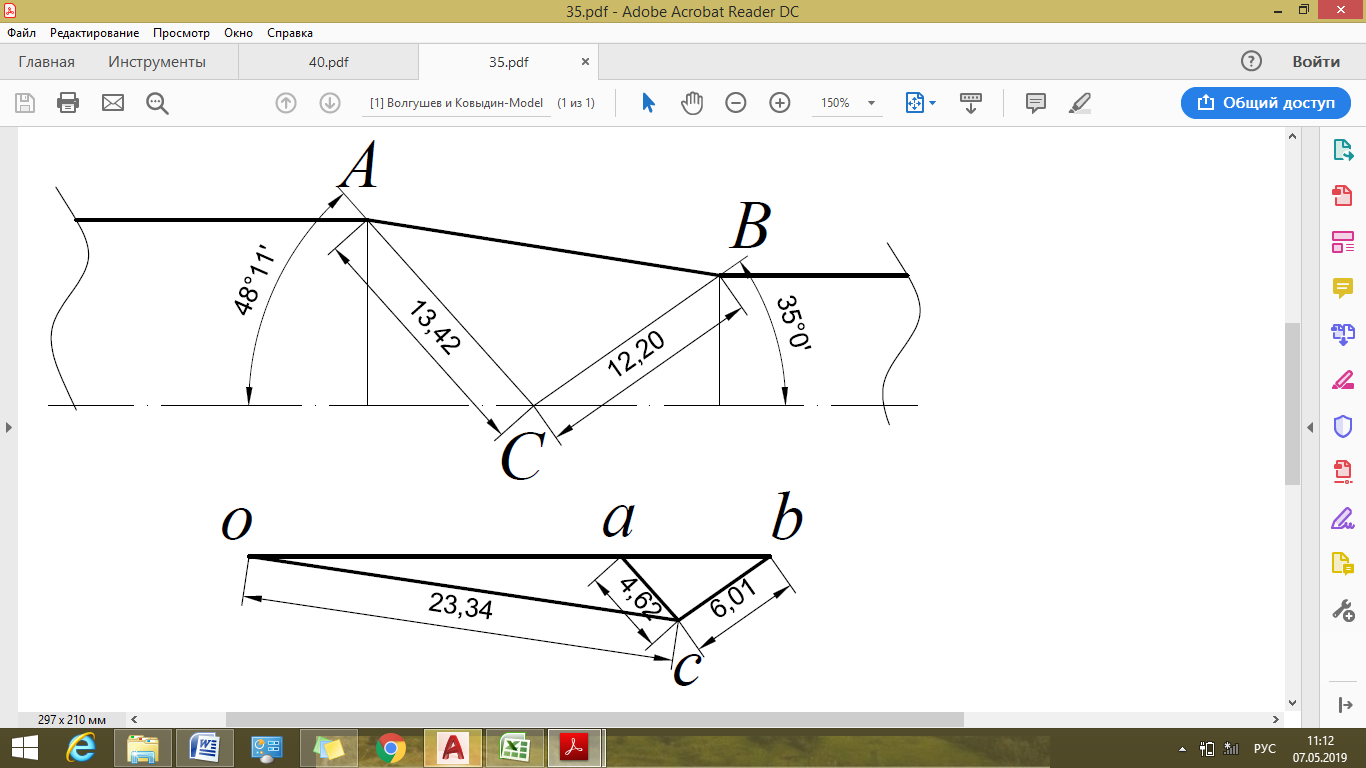
Рисунок 10 – Годограф скоростей (вариация №3)
Рисунок 11 – Годограф скоростей (вариация №4)
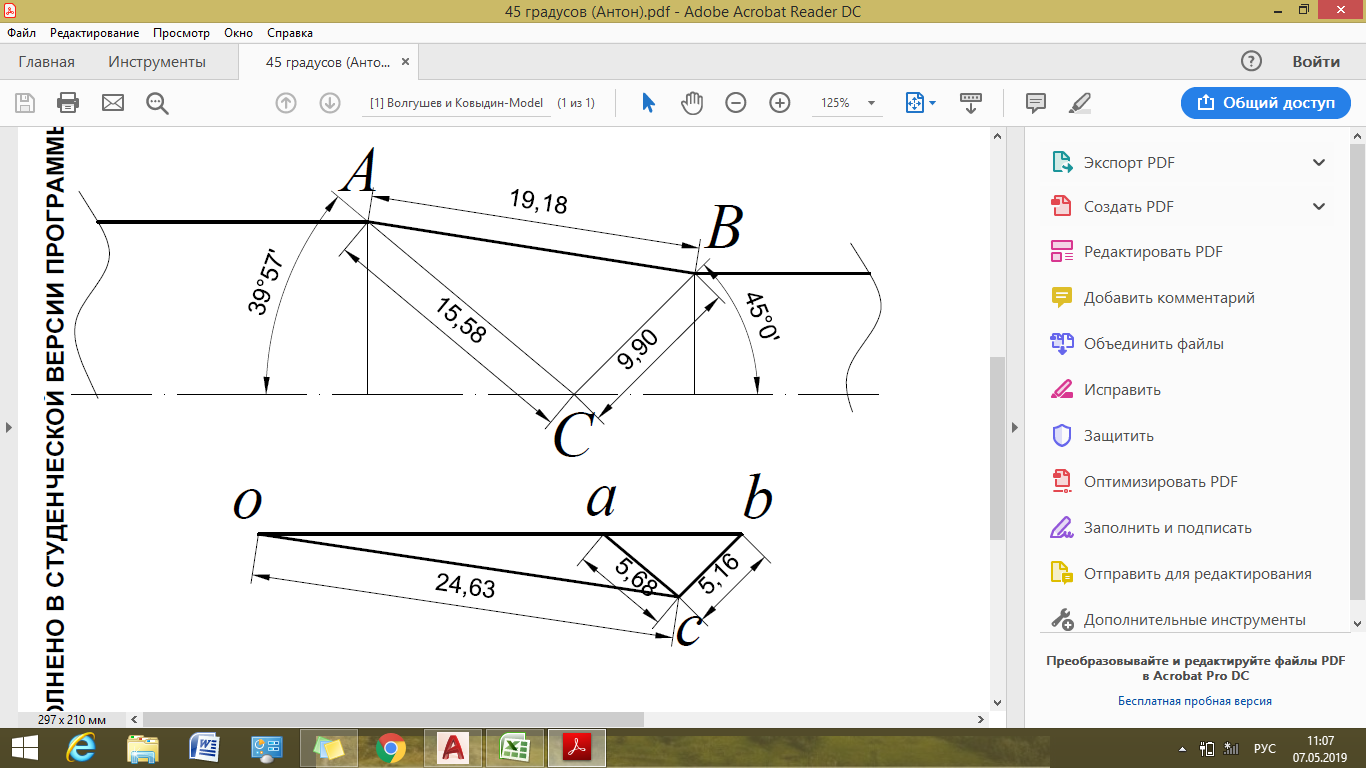
Рисунок 12 – Годограф скоростей (вариация №5)
Варьируя значения угла 
и измеряя стороны годографа, определим оптимальное значение угла , при котором достигается минимальное значение 
.
В таблице 10 предоставлены экспериментальные значения 
.
Таблица 10– Экспериментальные значения
| ,
| ,˚
| АС, мм | аc, мм | BC, мм | bc, мм | AB, мм | оc, мм | 
|
| 68,33 | 10,74 | 3,39 | 16,56 | 7,46 | 19,18 | 21,47 | 0,723175 | |
| 55,43 | 12,1 | 4,01 | 6,63 | 19,18 | 22,5 | 0,690832 | ||
| 48,11 | 13,42 | 4,62 | 12,2 | 6,01 | 19,18 | 23,34 | 0,687808 | |
| 43,2 | 14,57 | 5,18 | 10,89 | 5,63 | 19,18 | 24,03 | 0,701663 | |
| 39,57 | 15,58 | 5,68 | 9,9 | 5,16 | 19,18 | 24,63 | 0,717601 |
Построим график с зависимостью 
от , рисунок 12.
Рисунок 13 – Зависимость от
Из всех кинематических возможных полей скоростей действительным будет то, при которой мощность силы волочения минимальна. Минимальное значение 0,687 принимается при равной 48 
. Следовательно угол 
является оптимальным.
ЗАКЛЮЧЕНИЕ
В ходе работы оценен показатель схемы напряженного состояния при сжатии цилиндрических образцов при атмосферном давлении и под воздействием всестороннего давления жидкости. В случае сжатия график 
располагается во II четверти. Зависимость убывающая. Она показывает, что рост сжимающих напряжений всегда повышает пластичность металла при прочих равных условиях.
Произведен расчет фестонообразования при вытяжке заготовки. Профиль изделия характеризуется наличием 4-х фестонов под углом 45° к направлению прокатки. При проектировании технологических режимов прокатки необходимо вначале, исходя из видов последующих операций формообразования листов и лент, определить эффективные значения показателей анизотропии, а затем обеспечить их формирование в процессе прокатки. При прокатке необходимо сформировать в листах и лентах такой состав текстуры, который обеспечит равные значения показателей анизотропии в различных направлениях плоскости листа, а следовательно, минимальное фестонообразование.
Построена геометрия очага деформации при волочении широкой полосы через клиновую волоку. При помощи вариационного метода для заданных условий определено минимальное напряжение волочения 
и угол, при котором оно достигается 
.