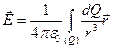,
где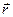 
- радиус-вектор, проведенный в рассматриваемую точку поля из точки нахождения малого заряда dQ.
Электростатическое поле – потенциально. Работа силы этого поля на любой замкнутой траектории равна нулю
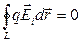или 
.
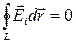Этот интеграл называется циркуляцией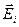 
вдоль замкнутого контура L.
Так как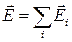 
, то 
.
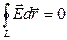Потенциальная энергия системы зарядов определяется формулой
.
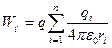Для непрерывно распределенных зарядов
.
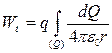Энергетической характеристикой поля служит потенциал.
Потенциалом электростатического поля называется физическая величина, равная отношению потенциальной энергии пробного точечного заряда, помещенного в рассматриваемую точку поля, к величине этого заряда
.
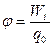Потенциал поля, создаваемого точечным зарядом
.
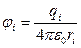Для системы из n зарядов
.
,
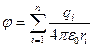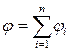т.е. при наложении электростатических полей их потенциалы складываются алгебраически.
Если заряды распределены непрерывно
.
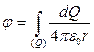Работа, совершаемая силами электростатического поля при перемещении точечного заряда q из точки 1 в точку 2
,
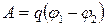где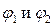 
- потенциалы поля, в точках 1 и 2 соответственно.
Если j 2 = 0, то
.
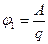Потенциал в какой-либо точке электростатического поля равен работе, совершаемой силами поля по перемещению заряда из этой точки поля в ту точку, где потенциал поля равен нулю.
Найдем связь между напряженностью и потенциалом электростатического поля.
,
,
,
.
.
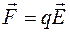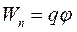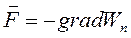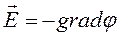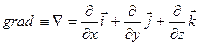Эквипотенциальная поверхность – геометрическое место точек электростатического поля, в которых значения потенциала одинаковы.
Существует два способа графического изображения электростатических полей – с помощью линий напряженности и с помощью эквипотенциальных поверхностей.
|
|
Эквипотенциальные линии представляют собой концентрические окружности, эквипотенциальные поверхности – концентрические сферы. Линии напряженности перпендикулярны эквипотенциальным поверхностям.
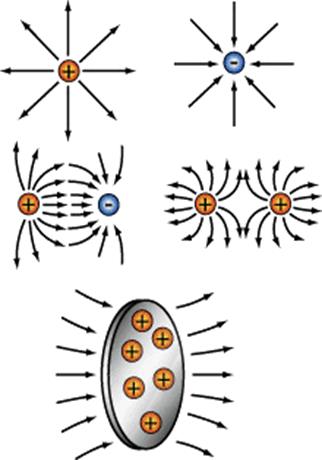
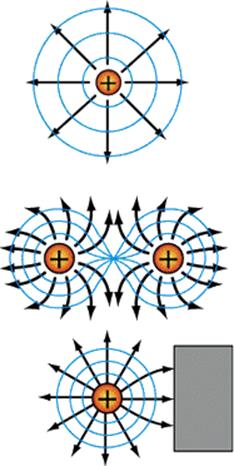
а) б)
Рис. Силовые линии (а) и эквипотенциальные поверхности (б) электростатического поля.
Демонстрация силовых линий поля
Электрический диполь – система, состоящая из двух точечных зарядов + q и
– q, расстояние между которыми мало по сравнению с расстоянием r до рассматриваемых точек ее поля.
 |
Рис. Электрический диполь.
Электрический дипольный момент – произведение +q на плечо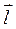 
.
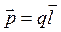Плечом диполя называется вектор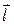 
, направленный по оси диполя от -q к +q и по модулю равный расстоянию между ними.
Если диполь поместить в однородное электрическое поле напряженностью
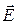, то на каждый из его зарядов будет действовать сила
,
.
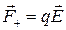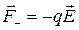Эти силы равны по модулю, но противоположны по направлению. Они создают момент пары сил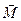 
.
 |
Рис. Диполь во внешнем поле.
,
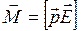M = q E l sina,
где a - угол между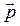 
и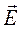 
.
В однородном поле момент пары сил стремится повернуть диполь так, чтобы 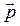и 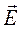были параллельны.
Определим 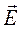в точке, лежащей посередине на оси диполя.
 |
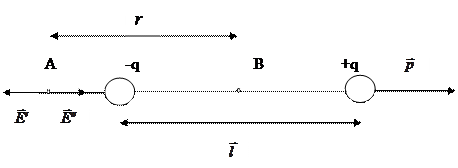На оси диполя между зарядами -q и +q векторы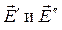 
направлены в одну сторону, поэтому результирующая напряженность по модулю равна их сумме.
Если находить напряженность в т.А, лежащей на продолжении оси диполя, то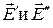 
направлены в разные стороны и результирующая напряженность
|
|
,
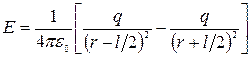где r – расстояние между средней точкой диполя и точкой, где определяется 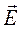. Пренебрегая (l /2)2, т.к. r >> l, получаем
,
.
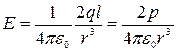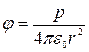Вычислим напряженность в т. С (рис.), лежащей на перпендикуляре, восстановленном из средней точки диполя. Так как r1 = r2, то
.
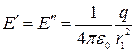Вектор результирующей напряженности в т.С равен
.
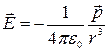j = 0.
 |
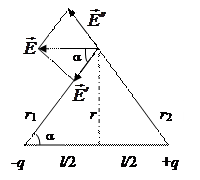Рис.
В произвольной точке (рис.)
,
.
 |
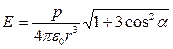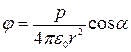Рис.
Число силовых линий, пронизывающих площадку dS, определяет поток вектора напряженности электрического поля.
 |
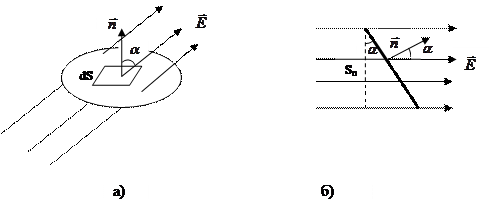Рис. Поток вектора напряженности электрического поля:
а) сквозь произвольную поверхность,
б) в случае плоской поверхности.
1. В общем случае поток вектора напряженности сквозь поверхность S равен (рис. а)
.
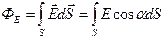2. Для однородного поля и плоской поверхности поток вектора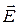 
равен
.
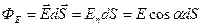Теорема Остроградского-Гаусса позволяет определить поток вектора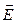 
, создаваемого системой зарядов.
Рассмотрим частный случай. Определим поток вектора 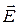сквозь сферическую поверхность радиуса r, в центре которой расположен точечный заряд + q.
.
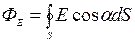Линии напряженности перпендикулярны поверхности сферы, значит cos a = 1.
 |
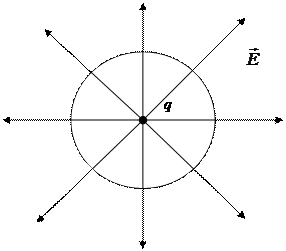Рис. Электрическое поле точечного заряда.
.
.
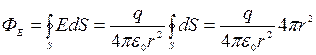
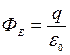