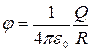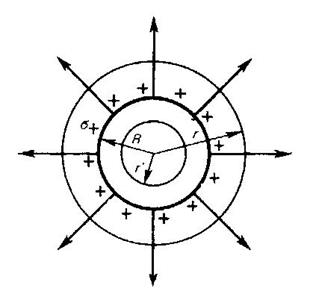
.
Рис.
2. Поле равномерно заряженного бесконечного цилиндра (нити).
Бесконечный цилиндр радиуса R заряжен равномерно с линейной плотностью t. Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности построим коаксиальный цилиндр радиуса r и высоты l. Поток вектора напряженности электрического поля сквозь торцы коаксиального цилиндра равен нулю, а сквозь боковую поверхность равен 2 prlE. По теореме Остроградского-Гаусса при r > R
.
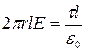Откуда
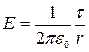, при r ³ R.
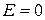, при r < R.
Разность потенциалов между двумя точками, лежащими на расстояниях r 1 и r 2 от оси заряженного цилиндра (r1 > R, r2 > R, r2 > r1), равна
.
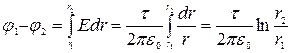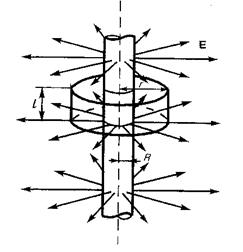
Рис.
3. Поле равномерно заряженной бесконечной плоскости.
Бесконечная плоскость (рис.) заряжена с постоянной поверхностной плотностью +s. Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cosa = 0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основании Еn совпадает с Е), т. е. равен 2 ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен s S. Согласно теореме Остроградского-Гаусса, 2 ES= s S/e0, откуда
.
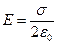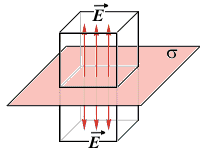
Рис.
Из этой формулы вытекает, что Е не зависит от длины цилиндра, т.е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.
Разность потенциалов между точками, лежащими на расстояниях x 1 и x 2 от плоскости, равна
.
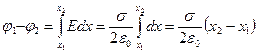4. Поле двух бесконечных параллельных равномерно заряженных плоскостей (рис.). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями + s и - s. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние - от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поли Е = 0.В области между плоскостями Е = Е+ + Е-_ (Е+ и Е- определяются по формуле (), поэтому результирующая напряженность
.
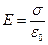Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой (), а вне объема, ограниченного плоскостями, равна нулю.
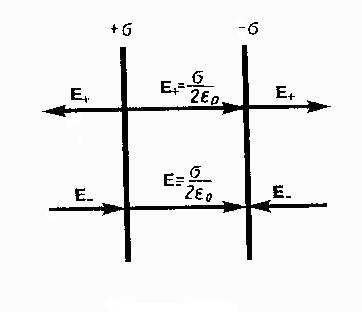
Рис.
Разность потенциалов между плоскостями, расстояние между которыми равно d, равна
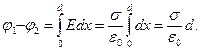
Выводы:
1. Напряженность электростатического поля в вакууме изменяется скачком при переходе через заряженную поверхность.
2. При переходе через границу области объемного заряда напряженность поля в вакууме изменяется непрерывно.
3. Потенциал поля всегда является непрерывной функцией координат.