Использование механических аналогов в расчётных моделях для определения нагрузок
В практике расчётов нагрузок широко используются механические аналоги, имитирующие динамическое поведение различных подсистем, элементов и агрегатов. Использование простых механических аналогов, описывающих автономные динамические свойства подсистем, позволяет существенно упростить расчётные схемы для определения нагрузок изделий в целом.
С этой целью в данном разделе построены механические аналоги типа осцилляторов, имитирующие продольные колебания стержневых подсистем, а также оболочек и осесимметричных упругих тел.
Отметим, что механические аналоги нашли широкое применение при анализе колебаний ёмкостей с жидким наполнителем (по динамике ёмкостей с жидкостью имеется большое количество исследований).
Остановимся на некоторых общих принципах построения механических аналогов для отдельных подсистем:
– в качестве аналогов выбираются простые механические системы, которые воспроизводят ту же совокупность кинематических и силовых факторов в сечениях связи, что и заменяемая подсистема, т.е. размерность и структура силового и кинематического подвекторов в сечениях соединения для механического аналога и заменяемой подсистемы должны быть идентичны;
– для построения механического аналога необходимо решить задачу о кинематическом возбуждении заменяемой подсистемы;
– динамическая часть решения задается в виде разложения в ряд по собственным формам колебаний закреплённой подсистемы (в кинематически возбуждаемых сечениях). Затем в результате использования обобщенного метода Галеркина получаются уравнения для обобщенных координат, на основе которых строятся механические аналоги;
– из условия равенства коэффициентов уравнения движения предлагаемого аналога и коэффициентов уравнения для обобщенных координат с использованием соответствующей нормировки форм колебаний подсистемы определяются параметры аналога. Отметим, что у построенных таким образом механических аналогов все инерционные характеристики совпадают с инерционными характеристиками заменяемой подсистемы, и они воспроизводят то же силовое воздействие на основную систему, что и заменяемая подсистема.
Механические аналоги, моделирующие продольные колебания стержней
Рассмотрим продольное кинематическое возбуждение стержня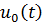 
через сечение 
. Верхнее сечение стержня свободное. На стержень могут действовать внешние распределённые и сосредоточенные силы 
.
| f (x,t) |
| e 1u0(t) |
| x |
| y |
Рисунок 9.1
Уравнение продольных колебаний стержня
| (9.1) |
где 
– погонная масса, 
– продольная жесткость.
Граничные условия
| (9.2) |
где 
– единичный вектор в направлении возбуждения (оси 
).
Будем искать решение в виде
 .
| (9.3) |
Уравнение для вновь введённой функции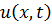 
примет вид
| (9.4) |
c граничным условием консольного стержня
| (9.5) |
Для удобства обобщения излагаемого подхода на пространственные системы величины, входящие в (9.1)-(9.4) 
будем считать одномерными векторами.
Отыскивая решение (9.4) в виде разложения по собственным формам колебаний консольного стержня 
| (9.6) |
с использованием процедуры Галеркина приходим к следующим уравнениям для обобщённых координат
  ,
| (9.7) |
где
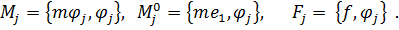
| (9.8) |
Отметим, что по структуре уравнения (9.7) аналогичны уравнению кинематически возбуждаемого осциллятора (рисунок9.2).
|
|
|
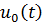
Рисунок 9.2
или
 .
| (9.9) |
Здесь 
и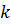 
– масса и жесткость осциллятора,
– растяжение пружины осциллятора,
– внешняя сила.
Для полной адекватности уравнений (9.7) и (9.9) необходимо обеспечить равенство всех коэффициентов уравнений и внешних сил.
С учётом (9.8) получаем
| (9.10) |
Из первого и третьего равенств (9.10) следует
| (9.11) |
Воспользуемся тем фактом, что формы колебаний определяются с точностью до константы в виде множителя и введём новые формы колебаний
| (9.12) |
Тогда из равенства (9.11) определим нормирующий множитель
| (9.13) |
С учётом введённых нормированных форм колебаний 
(9.12) и (9.13) параметры осциллятора (9.10), моделирующего колебания стержня по j -ому тону, примут вид
| (9.14) |
В случае использования нормированных по единичной массе форм колебаний 
формулы (9.14) для параметров осциллятора упрощаются
  .
| (9.15) |
Покажем, что сумма масс осцилляторов стремится к физической массе стержня.
Разложим единичный вектор по ортонормированным формам колебаний
| (9.16) |
Умножаем левую и правую части (9.16) на погонную массу стержня
| (9.17) |
Перемножаем скалярно левые и правые части равенств (9.16) и (9.17)
| (9.18) |
С учётом ортогональности собственных форм колебаний и определения обобщенного скалярного произведения для стержня будем иметь
| (9.19) |
То есть, суммарная масса осцилляторов равна в пределе физической массе стержня (равенство Парсеваля-Бесселя для коэффициентов Фурье-разложения).
Чтобы судить о характере сходимости приведённых параметров (9.14), (9.15), рассмотрим однородный стержень при продольных колебаниях. Формы колебаний в случае консольно закреплённого стержня имеют вид
  ,
| (9.20) |
где l – длина стержня.
Выполняя интегрирование в формуле (9.14) с учётом равенства (9.20), получим
| (9.21) |
Из выражения (9.21) видно, что первый член ряда (9.19) составляет 81% от физической массы стержня 
.