Приложение 2
Образец решения
Индивидуального задания
Вариант 1
Задание 1. Вычислить:
1)  ; 2)
; 2) 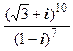 ; 3)
; 3) 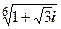 .
.
Решение. 1) Вычислим значение выражения по действиям:
I. (2-4 i)3=[применяем формулу куба разности]=
=23-3×22×4 i +3×2×(4 i)2-(4 i)3=8-12 i -96+64 i =-88+52 i.
II. (2- i)3=[аналогично предыдущему]=
=23-3×22× i +3×2× i 2- i 3=8-12 i -6+ i =2-11 i.
III. (2-4 i)3+(2- i)3=(-88+52 i)+(2-11 i)=(-88+2)+(52-11) i =-86+41 i.
IV. (3+2 i)3=[по формуле квадрата суммы]=
=32+2×3×2 i +(2 i)2=9+12 i -4=5+12 i.
V.  =
=  =
= 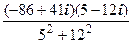 =
=
= 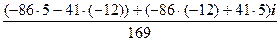 =
= 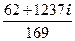 =
= 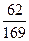 +
+ 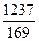 i.
i.
2) Вычислим и числитель, и знаменатель отдельно, применяя формулу Муавра. Для этого каждое из чисел 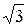 + i и 1- i приведём к тригонометрической форме. Имеем
+ i и 1- i приведём к тригонометрической форме. Имеем
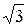 + i =2(cos
+ i =2(cos 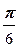 + i sin
+ i sin 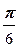 ),
),
Так как
| 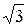 + i |=
+ i |= 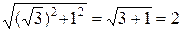 и
и 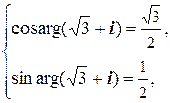
то есть 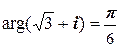 . Поэтому, по формуле Муавра,
. Поэтому, по формуле Муавра,
(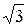 + i)10=(2(cos
+ i)10=(2(cos 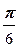 + i sin
+ i sin 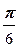 ))10=210(cos
))10=210(cos  + i sin
+ i sin  )=
)=
=210(cos 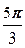 + i sin
+ i sin 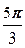 )=210(
)=210( -
- 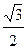 i)=29(1-
i)=29(1- 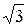 i).
i).
Аналогично
1- i = 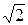 (cos
(cos  + i sin
+ i sin  ),
),
так как
|1- i |= 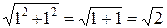 и
и 
то есть  . Тогда
. Тогда
(1- i)7= 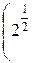 (cos
(cos 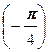 + i sin
+ i sin 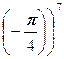 =
= 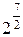 (cos
(cos 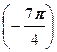 + i sin
+ i sin  =
=
= 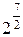 (cos
(cos  - i sin
- i sin 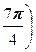 =
= 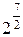
 +
+ 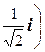 =
= 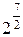 ×
×  (1+ i)=23(1+ i).
(1+ i)=23(1+ i).
Поэтому
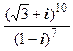 =
= 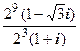 =26×
=26×  =26×
=26× 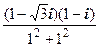 =25×(1-
=25×(1- 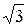 i)(1- i)=
i)(1- i)=
=25×((1- 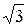 )+(-1-
)+(-1- 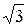 ) i)=25×((1-
) i)=25×((1- 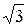 )-(1+
)-(1+ 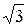 ) i)=32(1-
) i)=32(1- 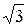 )-32(1+
)-32(1+ 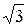 ) i.
) i.
3) Всего комплексных чисел 6-й степени из комплексного числа существует в точности 6. Их ищем в виде
w k = 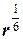 (cos
(cos 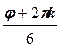 + i sin
+ i sin 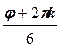 ), k =0, 1, 2, 3, 4, 5.
), k =0, 1, 2, 3, 4, 5.
Здесь r =  - модуль числа 1+
- модуль числа 1+ 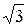 i, j =
i, j = 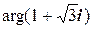 - аргумент этого числа, который находим из соотношения
- аргумент этого числа, который находим из соотношения
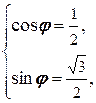
Поэтому j = 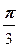 . Таким образом, корни -
. Таким образом, корни -
w k = 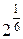 (cos
(cos 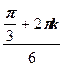 + i sin
+ i sin 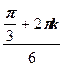 )=
)= 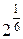 (cos
(cos 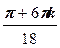 + i sin
+ i sin 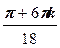 ), k =0, 1, 2, 3, 4, 5.
), k =0, 1, 2, 3, 4, 5.
Найдём их при каждом значении k:
w 0= 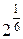 (cos
(cos 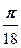 + i sin
+ i sin 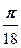 ), w 1=
), w 1= 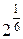 (cos
(cos 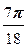 + i sin
+ i sin 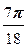 ), w 2=
), w 2= 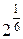 (cos
(cos 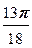 + i sin
+ i sin 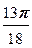 ),
),
w 3= 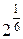 (cos
(cos 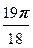 + i sin
+ i sin 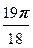 ), w 4=
), w 4= 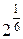 (cos
(cos 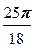 + i sin
+ i sin 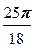 ), w 2=
), w 2= 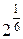 (cos
(cos 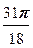 + i sin
+ i sin 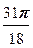 ).
).
(Значения косинусов и синусов - не табличные. Поэтому их значения не вычисляем, и корни не приводим к алгебраической форме).
Ответ: 1) 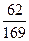 +
+ 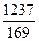 i; 2) 32(1-
i; 2) 32(1- 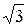 )-32(1+
)-32(1+ 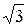 ) i;
) i;
2) w 0= 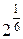 (cos
(cos 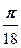 + i sin
+ i sin 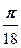 ), w 1=
), w 1= 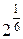 (cos
(cos 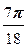 + i sin
+ i sin 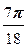 ),
),
w 2= 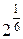 (cos
(cos 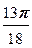 + i sin
+ i sin 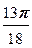 ), w 3=
), w 3= 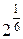 (cos
(cos 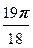 + i sin
+ i sin 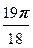 ),
),
w 4= 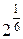 (cos
(cos 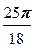 + i sin
+ i sin 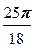 ), w 2=
), w 2= 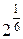 (cos
(cos 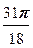 + i sin
+ i sin 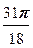 ).
).
Задание 2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) | z +1+2 i |³1; 2) | z -2+ i |<3.
Решение. 1) Пусть z = x + yi, где x =Re z и y =Im z. Тогда z +1+2 i =(x +1)+(y +2) i и | z +1+2 i |=  . Поэтому | z +1+2 i |³1 Û
. Поэтому | z +1+2 i |³1 Û  ³1 Û
³1 Û 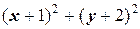 ³1. Получили множество точек, лежащих вне круга с центром (-1; -2) и радиусом R =1.
³1. Получили множество точек, лежащих вне круга с центром (-1; -2) и радиусом R =1.
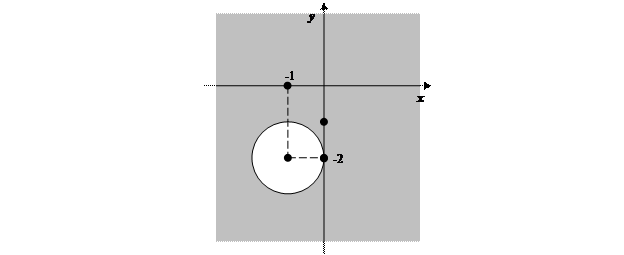
2) Аналогично предыдущему, если z = x + yi, то | z -2+ i |= 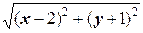 и | z -2+ i |<3 Û
и | z -2+ i |<3 Û 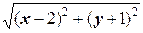 <3 Û
<3 Û 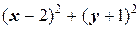 <9 ¾ внутренность круга с центром (2; -1) радиуса 3.
<9 ¾ внутренность круга с центром (2; -1) радиуса 3.
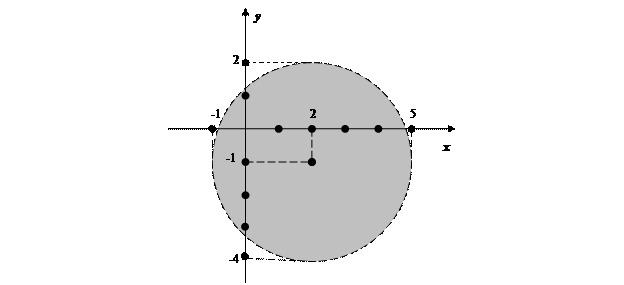
Задание 3. Разделить многочлен f (x) = x 5-2 x 3+ x 2+4 x +1 на многочлен g (x) = x 3-3 x 2+ x -2 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
Решение. Делим многочлен на многочлен с остатком:
| _x 5 -2 x 3+ x 2+4 x +1 | x 3-3 x 2+ x -2 | ||||||
| x 5-3 x 4+ x 3-2 x 2 | x 2+3 x +6 | ||||||
| _ 3 x 4-3 x 3+3 x 2+4 x +1 | |||||||
| 3 x 4-9 x 3+3 x 2-6 x | |||||||
| _ 6 x 3 +10 x +1 | |||||||
| 6 x 3-18 x 2+6 x -12 | |||||||
| 18 x 2+4 x +13 | |||||||
Таким образом, x 2+3 x +6 - неполное частное, 18 x 2+4 x +13 - остаток от деления x 5-2 x 3+ x 2+4 x +1 на x 3-3 x 2+ x -2.
Ответ: x 5-2 x 3+ x 2+4 x +1=(x 3-3 x 2+ x -2)(x 2+3 x +6)+(18 x 2+4 x +13), где x 2+3 x +6 - неполное частное, 18 x 2+4 x +13 - остаток
Задание 4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
 .
.
Решение. По правилу разложения дроби в сумму простейших имеем
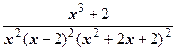 =
= 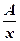 +
+ 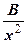 +
+ 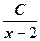 +
+  +
+ 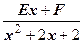 +
+ 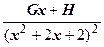
(так как дискриминант квадратного трёхчлена х 2+2 х +2 меньше нуля (D =22-4×1×2=-4<0), то дроби 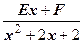 и
и 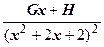 - простейшие).
- простейшие).
Приведём полученную сумму к общему знаменателю:

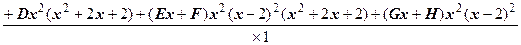 .
.
Отдельно приведём числитель к стандартному виду. Так как
(х 2+2 х +2)2= х 4+4 х 2+4+4 х 3+4 х 2+8 х = х 4+4 х 3+8 х 2+8 х +4
то имеем
x (x -2)2(х 2+2 х +2)2=(х 3-4 х 2+4 х)(х 4+4 х 3+8 х 2+8 х +4)=
= х 7+(4-4) х 6+(8-16+4) х 5+(8-32+16) х 4+(4-32+32) х 3+(-16+32) х 2+16 х =
= х 7-4 х 5-8 х 4+4 х 3+16 х 2+16 х,
(x -2)2(х 2+2 х +2)2= х 6-4 х 4-8 х 3+4 х 2+16 х +16
(это произведение отличается от предыдущего только на множитель х)
x 2(x -2)(х 2+2 х +2)2=(х 3-2 х 2)(х 4+4 х 3+8 х 2+8 х +4)=
= х 7+(4-2) х 6+(8-8) х 5+(8-16) х 4+(4-16) х 3-8 х 2=
= х 7+2 х 6-8 х 4-12 х 3-8 х 2,
x 2(х 2+2 х +2)2= х 6+4 х 5+8 х 4+8 х 3+4 х 2,
(Ex + F) x 2(x -2)2(х 2+2 х +2)=(Ex + F)(х 6-2 х 5-2 х 4+8 х 2)=
= Eх 7+(-2 E + F) х 6-(2 E +2 F) х 5-2 Fх 4+8 Eх 3,
(Gx + H) x 2(x -2)2=(Gx + H)(х 4-4 х 3+4 х 2)= Gх 5+(-4 G + H) х 4+(4 G -4 H) х 3.
Отсюда
Ax (x -2)2(х 2+2 х +2)2+ B (x -2)2(х 2+2 х +2)2+ Cx 2(x -2)(х 2+2 х +2)2+
+ Dx 2(х 2+2 х +2)2+(Ex + F) x 2(x -2)2(х 2+2 х +2)+(Gx + H) x 2(x -2)2=
= Aх 7-4 Aх 5-8 Aх 4+4 Aх 3+16 Aх 2+16 Aх + Bх 6-4 Bх 4-8 Bх 3+4 Bх 2+16 Bх +16 B +
+ Cх 7+2 Cх 6-8 Cх 4-12 Cх 3-8 Cх 2+ Dх 6+4 Dх 5+8 Dх 4+8 Dх 3+4 Dх 2+
+ Eх 7+(-2 E + F) х 6-(2 E +2 F) х 5-2 Fх 4+8 Eх 3+ Gх 5+(-4 G + H) х 4+(4 G -4 H) х 3=
=(A + C + E) х 7+(B +2 C + D -2 E + F) x 6+(-4 A +4 D -2 E -2 F + G) х 5+
+(-8 A -4 B -8 C +8 D -2 F -4 G + H) х 4+(4 A -8 B -12 C +8 D +8 E +4 G -4 H) х 3+
+(16 A +4 B -8 C +4 D) х 2+(16 A +16 B) х +16 B.
Поэтому
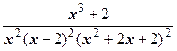 =
=

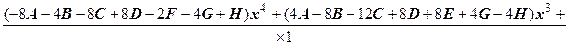
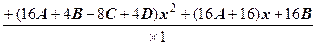
Дроби с одинаковыми знаменателями равны тогда и только тогда, когда совпадают их числители:
x 3+2º(A + C + E) х 7+(B +2 C + D -2 E + F) x 6+(-4 A +4 D -2 E -2 F + G) х 5+
+(-8 A -4 B -8 C +8 D -2 F -4 G + H) х 4+(4 A -8 B -12 C +8 D +8 E +4 G -4 H) х 3+
+(16 A +4 B -8 C +4 D) х 2+(16 A +16 B) х +16 B.
Два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной. Поэтому, приравнивая коэффициенты при одинаковых степенях переменной х, приходим к системе
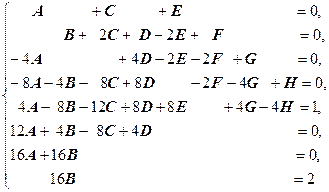 (*)
(*)
решая которую (например, методом Гаусса) определяем коэффициенты A, B, C, D, E, F, G, H.
Ответ: 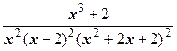 =
=
=  +
+ 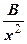 +
+ 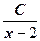 +
+  +
+  +
+ 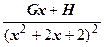 ;
;
требуемая система (*) приведена выше.
Задание 5. Представить дробь в виде суммы многочлена и простейших дробей:
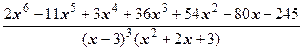 .
.
Решение. Степень знаменателя 5 меньше степени числителя (шести). Поэтому дробь является неправильной, и её можно представить в виде суммы многочлена и простейших дробей. Для этого сначала разделим числитель на знаменатель (с остатком), предварительно произведя умножения в знаменателе:
(x -3)3(х 2+2 х +3)=(х 3-9 х 2+27 х -27)(х 2+2 х +3)=
= х 5+(2-9) х 4+(3-18+27) х 3+(-27+54-27) х 2+(81-54) х -81=
= х 5-7 х 4+12 х 3+27 х -81,
| _ 2 x 6-11 x 5+ 3 x 4+36 x 3+54 x 2- 80 x -245 | x 5-7 x 4+12 x 3+27 x -81 | |||||
| 2 x 6-14 x 5+24 x 4+ +54 x 2-162 x | 2 x +3 | |||||
| _ 3 x 5-21 x 4+36 x 3 +82 x -245 | ||||||
| 3 x 5-21 x 4+36 x 3 +81 x -243 | ||||||
| x -2 | ||||||
Таким образом,
2 x 6-11 x 5+3 x 4+36 x 3+54 x 2-80 x -245=(2 x +3)(x 5-7 x 4+12 x 3+27 x -81)+(x -2),
откуда
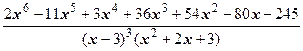 =
=
= 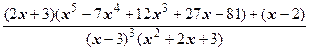 =
=
=  =(2 x +3)+
=(2 x +3)+ 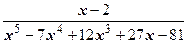 =
=
=(2 x +3)+  ,
,
то есть 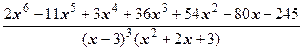 =(2 x +3)+
=(2 x +3)+  , и исходная дробь представлена в виде суммы многочлена и правильной дроби. Осталось представить слагаемое-дробь
, и исходная дробь представлена в виде суммы многочлена и правильной дроби. Осталось представить слагаемое-дробь 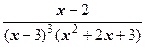 в виде суммы простейших.
в виде суммы простейших.
По правилу разложения дроби в сумму простейших имеем
 =
= 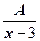 +
+  +
+ 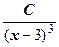 +
+  (*)
(*)
(так как дискриминант квадратного трёхчлена х 2+2 х +3 меньше нуля (D =22-4×1×3=-8<0), то дробь  - простейшая).
- простейшая).
Приведём полученную сумму к общему знаменателю:
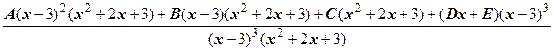 .
.
Отдельно приведём числитель к стандартному виду.
A (x -3)2(х 2+2 х +3)+ B (x -3)(х 2+2 х +3)+ C (х 2+2 х +3)+(Dx + E)(x -3)3=
= A (х 4- х 3+27)+ B (х 3- х 2-3 х -9)+ C (х 2+2 х +3)+(Dx + E)(x 3-9 х 227 х -27)=
=(A + D) х 4+(- A + B -9 D - E) х 3+(- B + C +27 D -9 E) х 2+
+(-3 B +2 C -27 D +27 E) х +(27 A -9 B +3 C -27 D).
Поэтому
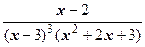 =
=

Дроби с одинаковыми знаменателями равны тогда и только тогда, когда совпадают их числители:
x -2º(A + D) х 4+(- A + B -9 D - E) х 3+(- B + C +27 D -9 E) х 2+
+(-3 B +2 C -27 D +27 E) х +(27 A -9 B +3 C -27 D).
Два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной. Поэтому, приравнивая коэффициенты при одинаковых степенях переменной х, приходим к системе

Решая эту систему определяем коэффициенты A, B, C, D, E. Сначала применим метод Гаусса для исключения неизвестных A, B, C из последних двух уравнений:
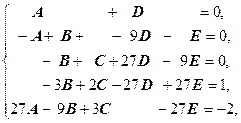 Û
Û 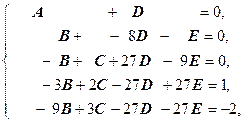 Û
Û
Û 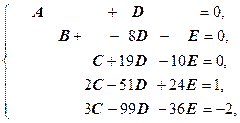 Û
Û 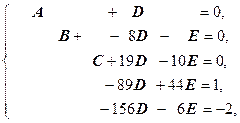
Далее, рассматривая последние два уравнения как систему от двух неизвестных D и E, находим их по правилу Крамера:
D= 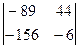 =(-89)×(-6)-(-156)×44=7398,
=(-89)×(-6)-(-156)×44=7398,
D1=  =1×(-6)-(-2)×44=82,
=1×(-6)-(-2)×44=82,
D2= 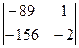 =(-89)×(-2)-(-156)×1=334,
=(-89)×(-2)-(-156)×1=334,
D = 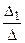 =
= 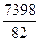 =
= 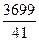 , E =
, E = 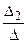 =
= 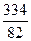 =
=  .
.
Теперь из третьего уравнения системы находим С:
C =-19 D +10 E =-19× 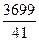 +10×
+10×  =
= 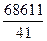 .
.
Из второго находим B:
B =8 D + E =8× 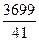 +
+  =
= 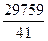 .
.
Наконец, из первого находим A:
A =- D =- 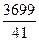 .
.
Таким образом, A =- 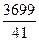 , B =
, B = 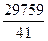 , C =
, C = 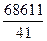 , D =
, D = 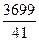 , E =
, E = 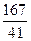 , подставляя которые в (*), получаем разложение дроби
, подставляя которые в (*), получаем разложение дроби 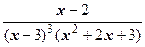 в сумму простейших:
в сумму простейших:
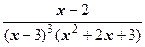 =
=  +
+ 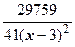 +
+ 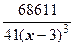 +
+ 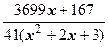 ,
,
а вместе с ним и искомое представление дроби в виде суммы многочлена и простейших.
Ответ: 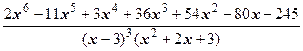 =
=
=(2 x +3)  +
+ 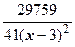 +
+ 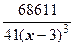 +
+ 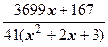 .
.
Приложение 3
Множество и способы его задания
Понятие множества является неопределяемым, то есть оно относится к основным понятиям, таким, как точка, прямая, плоскость. Это понятие можно пояснить, например, как совокупность объектов, обладающих определенным свойством. Так, можно рассматривать множество людей, живущих на Земле, множество студентов данного учебного заведения, множество точек на отрезке, множество дисциплин, по которым сдаются экзамены в данную сессию и т.д. Объекты, из которых состоит множество, называются элементами этого множества.
Множество может не содержать ни одного элемента (например, множество круглых квадратов). Такое множество называется пустым и обозначается через Æ. Кроме пустого множества рассматривается так называемое универсальное множество U, которое содержит в качестве подмножеств все множества данного контекста. Например, если рассматриваются числовые множества, то в качестве U можно рассматривать такое числовое множество, которое содержит все эти множества. Так, если рассматриваются числовые множества, состоящие из действительных чисел (например, числовые интервалы), то в качестве U можно взять множество R всех действительных чисел.
Множества принято обозначать через заглавные буквы латинского алфавита (возможно, снабжённые индексами): A, B, C, …, X, Y, Z, …, A 1, A 2, …. Элементы множества обозначаются через строчные (также, возможно, с индексами): a, b, c, …, а 1, а 2, …. Тот факт, что a является элементом множества A обозначается через a Î A. Если а не является элементом множества А, то это обозначается через a Ï A.
Если из a Î A следует a Î B, то A называется подмножеством множества B. Тот факт, что A является подмножеством множества B, обозначается через A Í B.
Пустое множество считается подмножеством любого множества.
Если одновременно выполняются условия A Í B и B Í A, то множества A и B называются равными. Тот факт, что множества A и B равны, обозначается через A = B.
Если A Í B, но A ¹ B, то А называется собственным подмножеством множестваВ, и обозначается через A Ì B.
Множество можно задать перечислением его элементов, заключая весь список элементов в фигурные скобки, или с помощью так называемого характеристического свойства. В первом случае это выглядит следующим образом: A ={ a 1, a 2, …, an, …}, где A - это множество, состоящее из элементов a 1, a 2, …, an, …. Во втором случае A ={ a | P (a)}. Это означает, что множество А состоит из таких элементов a, которые удовлетворяют некоторому условию P (a). P (a) - характеристическое свойство.