Лабораторная работа № 2.2
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА
Ознакомьтесь с теорией в конспекте и учебниках. Запустите программу «Открытая физика 1.1». Выберите раздел «Термодинамика и молекулярная физика» и работу «Распределение Максвелла». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите необходимое в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.
Целью работы является изучение на компьютерной модели максвелловского распределения молекул идеального газа по величинам скоростей.
Содержанием работы является:
• Получение на основе компьютерной модели максвелловского распределения молекул газа по скоростям при различных температурах.
• Изучение зависимости наиболее вероятной скорости молекул газа от температуры.
• Определение массы молекул в данной модели.
Краткая теория
Молекулярная физика изучает системы, состоящие из очень большого числа частиц. Наиболее простой моделью системы многих частиц является идеальный газ. Эта система состоит из большого числа точечных материальных объектов с конечной массой, находящихся в состоянии непрерывного хаотичного движения. Частицы не взаимодействуют друг с другом на расстоянии. При столкновении ведут себя как упругие шары. Наиболее близко свойствам идеального газа соответствуют обычные газы при условиях, не сильно отличающихся от нормальных  .
.
Простота модели идеального газа делает ее удобной для ознакомления со статистическим методом описания систем многих частиц. В его основе лежат следующие представления:
- свойства системы в целом определяются свойствами и характером движения частиц, ее составляющих;
- в силу многочисленности частиц и большого числа столкновений их поведение носит случайный характер;
- поведение системы в целом необходимо описывать не совокупностью координат и скоростей частиц, а усредненными характеристиками (средняя энергия, средняя плотность и т.д.). При сопоставлении этих усредненных характеристик с термодинамическими соотношениями выясняется смысл микроскопических параметров системы. Так, например, оказалось, что абсолютная температура пропорциональна средней кинетической энергии поступательного движения молекул.
Закономерности, получаемые статистическим методом, называются вероятностными, или статистическими. Для их получения строится модель изучаемой системы.
В данной работе рассматривается применение статистического метода описания к вопросу о распределении молекул газа по скоростям в состоянии равновесия при  , в отсутствие внешних силовых полей. Опыт показывает, что любая изолированная система приходит в состояние теплового (термодинамического) равновесия, в котором ее макроскопические параметры (давление, температура) не изменяются со временем и постоянны в объеме. Но согласно основным представлениям молекулярно-кинетической теории молекулы системы находятся в беспорядочном хаотическом движении. В идеальном газе молекулы движутся между столкновениями поступательно с разными скоростями, изменяя скорость при столкновении. В этом случае случайной величиной (разной у молекул) является скорость и стоит задача о нахождении распределения молекул газа по скоростям. Для этого необходимо принять модель системы и качественно рассмотреть свойства этой системы в состоянии теплового равновесия.
, в отсутствие внешних силовых полей. Опыт показывает, что любая изолированная система приходит в состояние теплового (термодинамического) равновесия, в котором ее макроскопические параметры (давление, температура) не изменяются со временем и постоянны в объеме. Но согласно основным представлениям молекулярно-кинетической теории молекулы системы находятся в беспорядочном хаотическом движении. В идеальном газе молекулы движутся между столкновениями поступательно с разными скоростями, изменяя скорость при столкновении. В этом случае случайной величиной (разной у молекул) является скорость и стоит задача о нахождении распределения молекул газа по скоростям. Для этого необходимо принять модель системы и качественно рассмотреть свойства этой системы в состоянии теплового равновесия.
Так как в состоянии равновесия давление во всех частях системы одинаково, то естественно допустить, что в газе отсутствуют какие-либо направленные движения молекул, то есть движения молекул предельно неупорядочены. В отношении скоростей молекулы это означает:
- скорость молекул и ее проекции являются непрерывными величинами, так как ни одно значение скорости не имеет преимущества перед другими значениями;
- при тепловом равновесии при  в газе все направления скоростей молекул равновероятны. В противном случае это привело бы к образованию направленных макроскопических потоков молекул и возникновению перепадов давления.
в газе все направления скоростей молекул равновероятны. В противном случае это привело бы к образованию направленных макроскопических потоков молекул и возникновению перепадов давления.
Так как скорость и ее проекции являются непрерывными величинами, вводится понятие функции плотности распределения  по компонентам скоростей молекул
по компонентам скоростей молекул  и по модулю скорости
и по модулю скорости  , называемая функцией распределения молекул по величинам скоростей
, называемая функцией распределения молекул по величинам скоростей  , была выведена теоретически, применяя методы теории вероятностей, Дж. Максвеллом в1859 году и носит его имя:
, была выведена теоретически, применяя методы теории вероятностей, Дж. Максвеллом в1859 году и носит его имя:

где  – масса одной молекулы,
– масса одной молекулы,  – постоянная Больцмана,
– постоянная Больцмана, 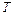 – температура,
– температура,  .
.
Максвелловская функция распределения  позволяет найти относительное число (относительную долю) молекул
позволяет найти относительное число (относительную долю) молекул 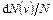 , величина скорости которых лежат в интервале от
, величина скорости которых лежат в интервале от  до
до  , то есть
, то есть  , откуда
, откуда 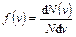 . В эквивалентной интерпретации – позволяет найти элементарную вероятность
. В эквивалентной интерпретации – позволяет найти элементарную вероятность  того, что модуль скорости произвольной молекулы окажется в пределах от
того, что модуль скорости произвольной молекулы окажется в пределах от  до
до  ,
,
 .
.
Таким образом,  имеет смысл плотности вероятности и позволяет вычислять средние значения любой физической величины, являющейся функцией от скорости молекул. Так, средняя арифметическая, или средняя скорость равна:
имеет смысл плотности вероятности и позволяет вычислять средние значения любой физической величины, являющейся функцией от скорости молекул. Так, средняя арифметическая, или средняя скорость равна:
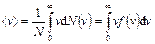 ;
;  .
.
Для средней квадратичной скорости получается формула:
 ;
;  .
.
Выражения для функций плотности вероятности по компонентам скоростей  имеют вид
имеют вид
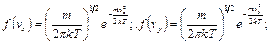

График функции  изображен на рис. 1.
изображен на рис. 1.
Функция  имеет максимум при скорости
имеет максимум при скорости  , симметрична относительно его и экспоненциально стремится к нулю при скорости
, симметрична относительно его и экспоненциально стремится к нулю при скорости  . Произведение
. Произведение  , где
, где  ‑ элементарный скоростной интервал около значений скоростей
‑ элементарный скоростной интервал около значений скоростей 
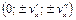 , равно доле молекул
, равно доле молекул  , компонента скорости
, компонента скорости  которых лежит в интервале около указанных значений. С другой стороны, произведение
которых лежит в интервале около указанных значений. С другой стороны, произведение  на графике равно заштрихованным площадкам
на графике равно заштрихованным площадкам  около выбранных скоростей.
около выбранных скоростей.

Рис.1. График функций плотности вероятности по компоненте скорости  .
.
Из сопоставления размеров заштрихованных площадей следует:
- относительное большинство молекул имеет проекцию скорости вдоль оси  , близкую к нулю;
, близкую к нулю;
- доли молекул, имеющих одинаковые значения  , но летящие в противоположных направлениях (разные знаки +
, но летящие в противоположных направлениях (разные знаки +  и -
и -  ), одинаковы;
), одинаковы;
- число молекул, имеющих большие значения компонент скоростей, мало (мала площадь около ±  ).
).
Аналогичный анализ можно провести и для 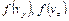 .
.
 Рис.2. Анализ зависимости
Рис.2. Анализ зависимости 
| Проанализировав зависимость функции распределения  от абсолютного значения скорости, можно заметить, что с ростом от абсолютного значения скорости, можно заметить, что с ростом  плотность вероятности с одной стороны растет за счет плотность вероятности с одной стороны растет за счет  , а с другой – убывает за счет экспоненты. Следовательно, функция распределения , а с другой – убывает за счет экспоненты. Следовательно, функция распределения  должна иметь максимум (см. рис. 2). должна иметь максимум (см. рис. 2).
|
Функция  равна 0 при скорости
равна 0 при скорости 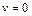 ; стремится к нулю при
; стремится к нулю при 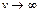 , при
, при 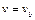 имеет максимум. Значение скорости
имеет максимум. Значение скорости 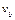 , при которой функция плотности распределения достигает максимума, называется наиболее вероятной скоростью, потому что вероятность обнаружить частицы в интервале длиной
, при которой функция плотности распределения достигает максимума, называется наиболее вероятной скоростью, потому что вероятность обнаружить частицы в интервале длиной  вблизи
вблизи 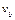 больше, чем вблизи любого другого значения скорости. Ее значение находится из условия экстремума
больше, чем вблизи любого другого значения скорости. Ее значение находится из условия экстремума 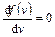 :
:  , где
, где 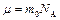 – молярная
– молярная
 Рис.3. Соотношение скоростей
Рис.3. Соотношение скоростей
| масса,  – пос-тоянная Авогадро, – пос-тоянная Авогадро,  – универсаль-ная газовая постоянная.
Сравнивая наиболее вероятную – универсаль-ная газовая постоянная.
Сравнивая наиболее вероятную  , среднюю , среднюю 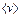 и среднеквадратичную
скорости и среднеквадратичную
скорости  , можно заметить, что , можно заметить, что  (см. рис. 3). (см. рис. 3).
|
Физический смысл. Произведение  дает долю молекул
дает долю молекул  , скорости которых лежат в выбранном интервале
, скорости которых лежат в выбранном интервале  . На графике (см. рис.4) это произведение равно площади заштрихованной полоски. Как видно из графика, максимальная площадка соответствует скорости
. На графике (см. рис.4) это произведение равно площади заштрихованной полоски. Как видно из графика, максимальная площадка соответствует скорости 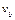 . С увеличением скорости доля молекул, обладающих большими скоростями, уменьшается (малая площадь при
. С увеличением скорости доля молекул, обладающих большими скоростями, уменьшается (малая площадь при  ).
).

Рис.4. График функции 
Как следует из явного вида распределения Максвелла по абсолютным значениям скорости 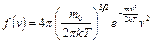 , распределение молекул по скоростям зависит от их массы и температуры газа, причем эти зависимости обратные
, распределение молекул по скоростям зависит от их массы и температуры газа, причем эти зависимости обратные

Рис.5. Зависимости функции распределения либо от массы молекул при T=const, либо от температуры газа при m=const.
На рис. 5 приведены функции распределения молекул по скоростям при разных массах молекулы  при
при  , или температурах газа
, или температурах газа 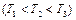 при
при  .
.
При повышении температуры наиболее вероятная скорость увеличивается, поэтому максимум кривой смещается в сторону больших скоростей. Площади, ограниченные кривыми и осью скоростей, равны единице (функция  удовлетворяет условию нормировки
удовлетворяет условию нормировки 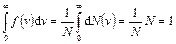 ) и не могут измениться при повышении температуры. Вследствие этого максимум функции распределения понижается по мере повышения температуры и становится менее острым.
) и не могут измениться при повышении температуры. Вследствие этого максимум функции распределения понижается по мере повышения температуры и становится менее острым.
Таким образом, закон Максвелла распределения молекул газа по скоростям описывает поведение очень большого числа частиц, то есть является статистическим законом. Распределение молекул по скоростям устанавливается посредством их столкновений. При столкновениях изменяются скорости отдельных молекул, но закон распределения по скоростям не изменяется.
Эту ситуацию можно понять следующим образом. Выделим среди молекул несколько скоростных групп, то есть групп молекул, скорости которых лежат в интервале  около значений
около значений  и так далее. Количество молекул в этих скоростных группах обозначим, соответственно, через
и так далее. Количество молекул в этих скоростных группах обозначим, соответственно, через 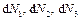 и т.д. При столкновении молекулы изменяют свою скорость и выбывают из своей скоростной группы в другую. Точно такое же количество молекул переходит в эту скоростную группу из других групп, так что в любой момент времени в состоянии теплового равновесия число молекул в каждой скоростной группе неизменно. Итак, за большой промежуток времени молекула, изменяя скорость при столкновениях, «переберет» все значения скоростей от малых до больших.
и т.д. При столкновении молекулы изменяют свою скорость и выбывают из своей скоростной группы в другую. Точно такое же количество молекул переходит в эту скоростную группу из других групп, так что в любой момент времени в состоянии теплового равновесия число молекул в каждой скоростной группе неизменно. Итак, за большой промежуток времени молекула, изменяя скорость при столкновениях, «переберет» все значения скоростей от малых до больших.
Методика и порядок измерений
Внимательно рассмотрите рисунок 6 и зарисуйте необходимое в свой конспект лабораторной работы.
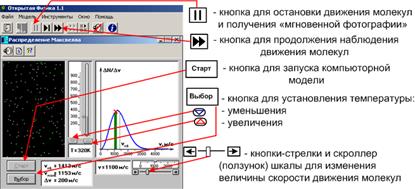
Рис. 6. Окно опыта
Внимательно рассмотрите изображение на экране монитора компьютера. Обратите внимание на систему частиц, движущихся в замкнутом объеме слева во внутреннем окне. Они абсолютно упруго сталкиваются друг с другом и со стенками сосуда. Их количество около N = 150 и данная система является хорошей «механической» моделью идеального газа. В процессе исследований можно останавливать движение всех молекул (при нажатии кнопки «çê » вверху) и получать как бы «мгновенные фотографии», на которых выделяются более ярким свечением частицы (точки), скорости которых лежат в заданном диапазоне  вблизи заданной скорости
вблизи заданной скорости  (т.е. имеющие скорости от
(т.е. имеющие скорости от  до
до  ). Для продолжения наблюдения движения частиц надо нажать кнопку «uu». Запишите в тетрадь значение
). Для продолжения наблюдения движения частиц надо нажать кнопку «uu». Запишите в тетрадь значение  , указанное на экране.
, указанное на экране.
Измерения
1. Нажмите кнопки «uu», «Старт» и «Выбор» и установите температуру Т 1, указанную в табл. 1 для вашей бригады. Для выбранной температуры запишите приведенные в окне значения средней 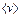 и квадратичной
и квадратичной  скоростей и определите примерный диапазон скоростей
скоростей и определите примерный диапазон скоростей  . Вблизи скоростей молекул
. Вблизи скоростей молекул  и
и 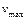 количество молекул (они более яркие) в замкнутом объеме слева во внутреннем окне опыта должно быть не менее 2-3-х молекул.
количество молекул (они более яркие) в замкнутом объеме слева во внутреннем окне опыта должно быть не менее 2-3-х молекул.
2. Установите скорость первой выделенной группы молекул вблизи минимального значения  . Исследуемый диапазон скоростей при этом будет находиться в интервале (от
. Исследуемый диапазон скоростей при этом будет находиться в интервале (от  до
до 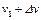 )
)
3. Нажмите клавишу «çê » и подсчитайте на «мгновенной фотографии» количество молекул  , скорости которых лежат в заданном диапазоне
, скорости которых лежат в заданном диапазоне  вблизи заданной скорости молекул
вблизи заданной скорости молекул  (они более яркие). Результат запишите в табл. 2.
(они более яркие). Результат запишите в табл. 2.
4. Увеличивая предыдущую скорость на 200 м/с и переходя к следующим диапазонам скоростей 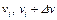 , где
, где  , повторите измерения (как в пункте 3).
, повторите измерения (как в пункте 3).
5. Определите общее количество молекул 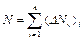 .
.
6. Выберите (как в пункте 1) еще два значения температуры  из табл.1 и для каждой температуры повторите измерения (по пунктам 1, 2, 3, 4, 5), записывая результаты в таблицы 3, 4, аналогичные табл. 2.
из табл.1 и для каждой температуры повторите измерения (по пунктам 1, 2, 3, 4, 5), записывая результаты в таблицы 3, 4, аналогичные табл. 2.
Таблица 1
Примерные значения температуры (не перерисовывать)
| Бригада | ||||||||

| ||||||||
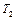
| ||||||||

|
Таблицы 2, 3, 4
Результаты измерений при 
 ;
; 
 ,км / с ,км / с
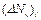
| 
| 
| 
| … | … | … | 
|

|

|