Б) Граф функционирования цифрового автомата

Графами называют взаимосвязь двух множеств состоящих из множества вершин и множества рёбер, индуцируемых (связанных) между собой.

Полный граф - это граф, не имеющий петель, кратности ребер, и все его вершины связаны между собой.

Неориентированный граф - граф, не имеющий указания направлений ребер, при переходе из одной вершины в другую.

Ориентированный (полный) граф - граф с ребрами, указывающими конкретное направление при переходе из одной вершины в другую.

Граф-дерево - это слабосвязанный граф, у которого если удалить одно ребро, то он распадается на два графа.

Граф функционирование цифрового автомата представлен на рис.5. Он отражает возможные переходы цифрового автомата.

В узлах графа записываются состояния автомата, стрелками показаны возможные переходы. Над стрелками указаны условия перехода. Выделенные стрелки соответствуют безусловным переходам.

а0 а1

а4 а2

а3

Из состояния а0 осуществляется безусловный переход в состояние а1, при этом выполняется микрокоманда Y1.

Из состояния а1 при условии х выполняется переход в а3, а при 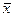осуществляется переход в состояние а2

Из состояния а2, и а3 осуществляются безусловные переходы в состояние а4

Из а4 выполняется безусловный переход в а0.

Теория графов имеет большие приложения, так как язык теории, с одной стороны, очевиден, а, с другой стороны, удобен в нормальном исследовании. При полном изображении графа не все детали рисунка имеют одинаковое значение, а именно геометрические свойства рёбер (кривизна, длина и т.д.) и расположение вершин на плоскости относительно друг друга.

Две вершины графа автомата а_т и a_s (исходное состояние и состояние перехода) соединяются дугой (ребром), направленной от а_т в a_s. Дуге (а_т, a_s) графа автомата приписывается входной сигнал х и выходной сигнал у, если он определён, и, в противном случае, ставится прочерк. Если переход автомата из состояния а_т в состояние a_s происходит под действием нескольких входных сигналов, то дуге (a_m, a_s) приписываются все эти входные и соответствующие выходные сигналы.

При описании автомата Мура в виде графа выходной сигнал y записывается внутри вершины а_т или рядом с ней, а входной сигнал х над дугой (ребром), демонстрирующей переход из одного состояния в другое.

При описании автомата Мили в виде графа внутри вершины записывается состояние, в которое переходит автомат, а над дугой (ребром), демонстрирующей переход из одного состояния автомата в другое, записывается дробь, в числителе которой указывается входной сигнал, а в знаменателе - выходной сигнал.

Для задания функций переходов и выходов построим граф-дерево автомата Мура, а затем автомата Мили. При использовании табличного описания автомата Мура таблицы переходов автоматов Мили и Мура совпадут, а таблица выходов автомата Мили получится из таблицы переходов заменой a_s символом выходного сигнала.

В технических целях используются только детерминированные цифровые автоматы, в которых выполнено условие однозначности переходов: - автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти более чем в одно состояние. Применительно к табличному способу задания описания автоматов это означает, что в клетках переходов/выходов указывается только по одному состоянию/выходному сигналу. Применительно к графическому способу задания описания автоматов это означает, что в графе автомата из любой вершины не могут выходить две или более дуги, отмеченные одним и тем же входным сигналом.

Устойчивым состоянием автомата называется такое состояние, что для любого х, d(a_m, x) = a_s, имеет место d(a_s, x) = a_s. Это значит, что если автомат перешёл в некоторое состояние х, то выйти из этого состояния может только под действием другого сигнала.

Синхронным называется автомат, если он не является асинхронным и каждое его состояние устойчиво. Если для некоторой пары (a_m, z_f) выходной сигнал автомата не определён, то для этой пары не определяется и функция перехода, так как не определено допустимое слово, осуществляющее переход из этого состояния.