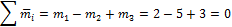Отсюда следует, что, во-первых, где бы не находилась точка О и, во-вторых, где бы не располагалась эта пара в теле и как бы она не была повёрнута в своей плоскости, действие её на тело будет одинаково. Так как момент сил, составляющих пару, в этих случаях один и тот же, равный моменту этой пары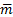 
.
3) Пару можно перемещать в пределах тела по плоскости действия и переносить в любую другую параллельную плоскость.
4) Так как действие на тело сил, составляющих пару, определяется лишь её моментом, произведением одной из сил на плечо, то у пары можно изменять силы и плечо, но так, чтобы момент пары остался прежним. Например, при силах F 1 =F 2 = 5 H и плече а = 4 см момент пары m = 20 H∙см. Можно силы сделать равными 2 Н, а плечо а = 10 см. При этом момент останется прежним 20 Н∙см и действие пары на тело не изменится.
Все эти свойства можно объединить и, как следствие, сделать вывод, что пары с одинаковым вектором момента 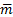и неважно где расположенные на теле, оказывают на него равное действие. То есть такие пары эквивалентны .
Исходя из этого, на расчётных схемах пару изображают в виде дуги со стрелкой, указывающей направление вращения, и рядом пишут величину момента m (рис. 6). Или, если это пространственная конструкция, показывают только вектор момента этой пары. И вектор момента пары можно прикладывать к любой точке тела. Значит вектор момента пары 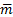– свободный вектор. Такое упрощенное изображение оправдано тем, что пара сил характеризуется моментом, а не ее положением в плоскости. Но если необходимо определять не внешние силы, а внутренние в разных сечениях элемента, как это делается в сопротивлении материалов, то важен знак и место приложения пары сил.
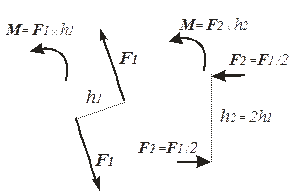
Рис.6. Эквивалентные пары сил
И ещё одно дополнительное замечание. Так как момент пары равен вектору момента одной из сил её относительно точки приложения второй силы, то момент пары сил относительно какой-либо оси z – есть проекция вектора момента пары 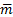на эту ось: 
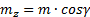, где 
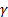– угол между вектором 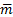и осью z.
Сложение пар
Пусть даны две пары с моментами m 1и m 2, расположенные в пересекающихся плоскостях (рис. 7).
Сделаем у пар плечи одинаковыми, равными а = АВ. Тогда модули сил, образующих первую пару, должны быть равны: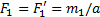 
, а образующих вторую пару: 
.
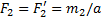Эти пары показаны на рис. 7, где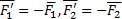 
. И расположены они в своих плоскостях так, что плечи пар совпадают с прямой АВ на линии пересечения плоскостей.
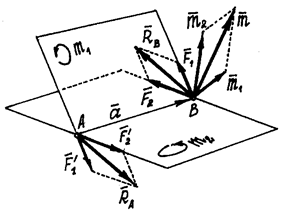
Рис.7. Пары сил с моментами m 1и m 2
Сложив силы, приложенные к точкам А и В, построением параллелограммов, получим их равнодействующие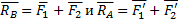 
. Так как 
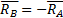, то эти силы 
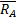и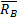 
будут образовывать пару, момент которой 
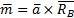, где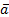 
– радиус-вектор точки В, совпадающий с АВ.
Так как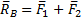 
, то момент полученной пары 
.
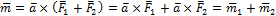Следовательно, в результате сложения пар, расположенных в пересекающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар.
При сложении нескольких пар, действующих в произвольных плоскостях, получим пару с моментом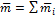 
.
Конечно, эта результирующая пара будет располагаться в плоскости перпендикулярной вектору .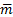
Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие равновесия пар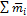 
=0.
Это является необходимым и достаточным условием равновесия систем пар.
Если пары расположены в одной плоскости, векторы моментов их будут параллельны. И момент результирующей пары можно определить как алгебраическую сумму моментов пар.
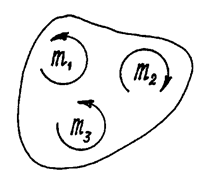
Рис.8. Моменты пар сил, расположенные в одной плоскости
Например, пары, показанные на рис.8, расположены в одной плоскости и моменты их:
m 1=2 Hсм, m 2=5 Hсм, m 3=3 Hсм. Пары уравновешиваются, потому что алгебраическая сумма их моментов равна нулю:
