Разрезная балка загружена сосредоточенными нагрузками. Нагрузки на балку передаются в местах опирания на нее вспомогательных балок. Сосредоточенные силы подсчитываются по грузовой площади:
Агр = Lв Lбн = 7× 2,5 = 17,5 м2
Сбор нагрузки на главную балку
Таблица 5
| Наименование нагрузки | Нормативная нагрузка, кН/м2 | gf | Расчетная нагрузка, кН/м2 | |
| Временная нагрузка Р = Рн × Агр = 12 × 17,5 | 210,0 | 1,2 | ||
| Собственный вес настила и балок Gбн = mgAгр=77,2×9,81×10-3 ×17,5 | 13,25 | 1,05 | 13,91 | |
| Собственный вес главной балки (3% от временной нагрузки) Gтр=0,02×210 | 6,3 | 1,05 | 6,615 | |
| Итого G+Р | 229,55 | 272,525 |
Коэффициент 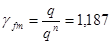
2.2.1. Подбор сечения главной балки
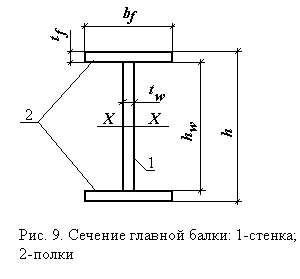
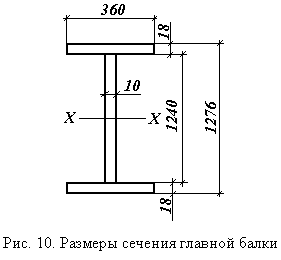
Сечение составной сварной балки состоит из трех листов: вертикального - стенки и двух горизонтальных - полок (рис. 9).
Расчетный изгибающий момент
Мmax = 9(G+P)Lбн - 4,5(G+P)Lбн = 4,5(G+P)Lбн = 4,5×272,525×2,5 = 3065,91 кН×м
Для принятой толщины листов полок tf ≤ 20 мм расчетное сопротивление стали С375 равно Rу =345 МПа. Коэффициент условия работы gс =1. В первом приближении с1 = 1,1.
 Требуемый момент сопротивления:
Требуемый момент сопротивления:

Высоту сечения балки h предварительно определим по соотношению между hоптW, hопт,f и hmin, где hоптW - оптимальная высота сечения из условия прочности; hопт,f - оптимальная высота сечения из условия жесткости; hmin - оптимальная высота сечения из условия минимальной жесткости, при обеспечении прочности.
1) оптимальная высота балки из условия прочности:
 ,
,
где 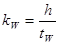 - отношения высоты балки к толщине стенки в пределах kW = 125…140. Принимаем kW = 130.
- отношения высоты балки к толщине стенки в пределах kW = 125…140. Принимаем kW = 130.
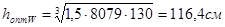
2) оптимальная высота балки из условия жесткости:
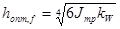 ,
,
где 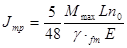 , n0 = 231,94 - для пролета L = 17,5 м
, n0 = 231,94 - для пролета L = 17,5 м
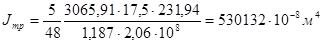

3) высота балки из условия минимальной жесткости при обеспечении прочности:
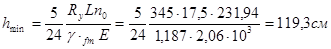
Выбор высоты балки
Т.к. hmin < hоптW < hопт,f, принимаем h = hоптW
Высота главной балки должна соответствовать наибольшей строительной высоте перекрытия согласно заданию:
h ≤ hc max - tн,
где tн - толщина настила.
Наибольшая строительная высота перекрытия определяется разностью отметок верха настила и габарита помещения под перекрытием:
hc max = 8,4 - 6,6 = 1,8 м
Т.к. h = 1199 см < hc max - tн = 1800 - 6 = 1794 мм - оставляем выбранную высоту h = 1199 см.
Принимаем толстолистовую сталь шириной 1250 мм. С учетом обрезки кромок с двух сторон по 5 мм hW = 1250 -10 = 1240 мм.
По коэффициенту kW = 130 определяем толщину стенки: tW = hW /kW = 1240/130 = 9, 5 мм. Принимаем tW =10 мм. Толщину полок назначим равной tf = 18 ≤ 3 tW = 30 мм.
Полная высота балки:
h = hW + 2 tf = 1240 + 2×18 = 1276 мм
Момент инерции стенки:

Требуемый момент инерции полок:
Jтр = Jтр max - JW,
где Jтр max определим по двум значениям из условий
а) прочности Jтр = 0,5Wтр h = 0,5×8848,2×127,6 = 564512,2 см4
б) жесткости Jтр = 530132 см4
Jтр = 564515,2 - 158885 = 405630,2 см4
Требуемая площадь сечения полки:
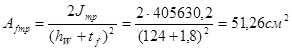
Толщина стенки из условия обеспечения ее местной устойчивости:
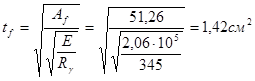
В расчете было принято 1,8 см, что больше tf = 1,42 см.
Ширину полки назначаем из условия 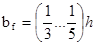 или bf = 427 …256 мм. Принимаем bf =360 мм, что соответствует ширине листа универсальной стали по сортаменту. Уточним собственный вес балки по принятым размерам.
или bf = 427 …256 мм. Принимаем bf =360 мм, что соответствует ширине листа универсальной стали по сортаменту. Уточним собственный вес балки по принятым размерам.
Площадь поперечного сечения:
А = 2Аf + АW = 2× 1,8 × 36 + 1,0×124 = 253,6 см2
Вес погонного метра балки:
gг = gS Аy = 77 × 0,02536×1,03 = 2,01 кН/м,
где gS = 77 кН/м - удельный вес стали;
y = 1,03 - конструктивный коэффициент, учитывающий вес ребер жесткости и сварных швов.
Вес главной балки на участке между вспомогательными балками:
Gг = gг Lбн = 2,01 × 2,5 = 5,025 кН
Уточним нагрузки на балку, полученные в табл.5.
Нормативная Рn + Gn = 210,0 + 13,25 + 5,025 = 228,275 кН
Расчетная Р + G = 252 + 13,9 + 5,33 = 271,23 кН
Уточним усилия. Изгибающие моменты от нормативных и расчетных нагрузок
Мn max = 4,5(Gn +Pn)Lбн = 4,5×228,275×2,5 = 2568,09 кН×м
Мmax = 4,5(G+P)Lбн = 4,5×271,23×2,5 = 3051,4 кН×м
Перерезывающая сила на опоре
Qmax = 3(G+P)= 3×271,23 = 813,69 кН
Геометрические характеристики сечения балки
Момент инерции
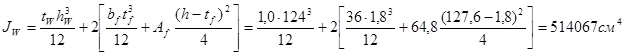
Момент сопротивления

Найдем отношение площадей полки и стенки
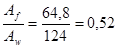
Найдем коэффициент с = 1,118. Т.к. в балке имеется зона чистого изгиба, принимаем с1 = с1m = 0,5(1+ с) = 1,059
2.2.2. Проверка прочности главной балки
1) Нормальные напряжения
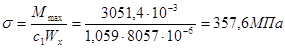 < Rg gс =379,5 МПа
< Rg gс =379,5 МПа
Недонапряжение не должно превышать 5%: (379,5-357,6)100% /379,5 = 5,1%
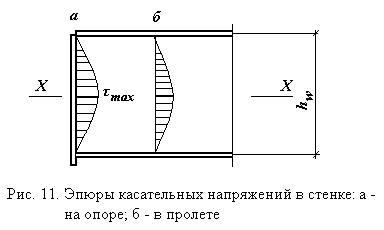 2) Касательные напряжения (проверяются в месте крепления опорного ребра без учета работы на срез полок
2) Касательные напряжения (проверяются в месте крепления опорного ребра без учета работы на срез полок
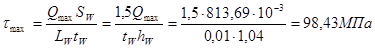
RS gс = 0,58×345×1=200,1 МПа - проверка удовлетворяется
2.2.3. Проверка прогиба главной балки.
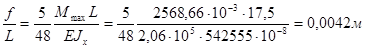
 - условие жесткости балки удовлетворяется.
- условие жесткости балки удовлетворяется.
2.2.4. Определение типа сопряжения вспомогательной и главной балок.
Суммарная высота элементов перекрытия: настила, балки настила, вспомогательной и главной балок
Sh= tН + hбн + hв + hг = 6 + 100 + 392 + 1276 = 1774 мм
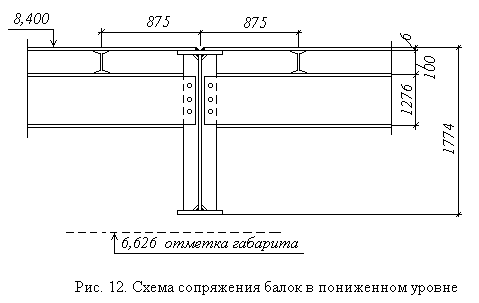 |
Ранее была найдена наибольшая строительная высота перекрытия hc,max = =1,8 м. Принимаем пониженное сопряжение вспомогательной и главной балок.
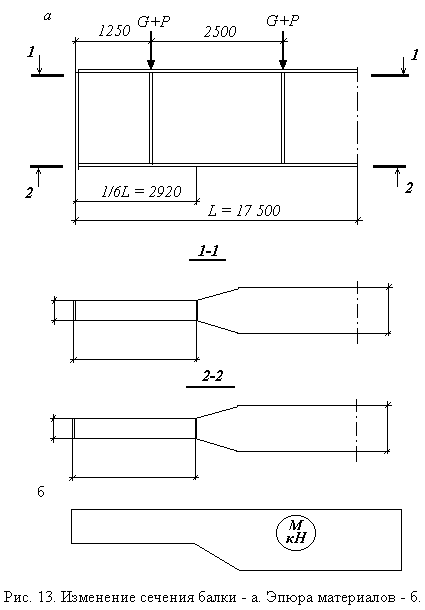
2.2.5. Изменение сечения главной балки.
С целью экономии материала уменьшаем сечение приопорного участка балки за счет уменьшения ширины поясов на участке балки от опоры до сечения, расположенного на расстоянии равном 1/6 пролета балки: 17,5/6 = 2,92 м. Ширина пояса балки b`f должна соответствовать ширине листа универсальной стали по сортаменту и быть не менее
b`f ³ 180мм, b`f ³ 0,1h; b`f ³ 0,5 bf,
т.е., 0,1h=127,6 мм; 0,5 bf = 0,5×360 = 180 мм.
По сортаменту принимаем b`f = 200 мм.
Геометрические характеристики сечения балки на приопорных участках:
- площадь сечения
А¢ = 2А¢f + АW = 2×20×1,8+1,0×124 = 196 см2
- момент инерции

- момент сопротивления
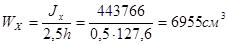
- статический момент полки относительно оси Х-Х
S¢Х = tf bf(0,5hW + 0,5tf) = 1,8 × 20 × 0,5(124+1,8) = 2264,4 см3
- статический момент полусечения относительно оси Х-Х
 |
SХ = S¢f +0,125× tW ×h2W = 2264,4+0.125×1242×1 = 4186,4 см3
Расчетные усилия в месте изменения сечения.
Изгибающий момент
М¢= Rа × 2,92 - (G+Р)(2,92-1,25)=3(G+Р) × 2,92-1,67(G+Р) = 7,09 (G+Р) = 7,09 × 271= 1923,0 кН
Перерезывающая сила
Q¢ = Qmax - (G+P)= 813,69 - 271,23 = 542,46 кН
Проверка напряжений
а) в месте изменения сечения
- максимальные нормальные напряжения
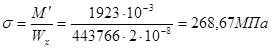
- касательные напряжения в стенке под полкой
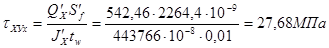 < RSgc = 0,58 × 315 × 1= 182,7 МПа
< RSgc = 0,58 × 315 × 1= 182,7 МПа
- приведенные напряжения под полкой

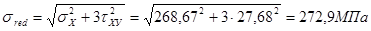
1,15 Rg gc = 1,15× 345 = 396,75 МПа
sred < 1,15 Rg gc
2.2.6. Расчет поясных сварных швов.
Полки составных сварных балок соединяют со стенкой на заводе автоматической сваркой. Сдвигающая сила на единицу длины
 ,
,
Для стали С375 по табл. 55* СНиП II-23-81* принимаем сварочную проволоку Св-10НМА для выполнения сварки под флюсом АН-348-А.
Определим требуемую высоту катета Кf поясного шва "в лодочку".
1. Расчет по металлу шва.
Коэффициент глубины провара шва bf =1,1 (СНиП II-23-81*, табл.34)
Коэффициент условия работы g wf = 1 (СНиП II-23-81*, пп. 11.2)
Расчетное сопротивление металла R wf =240 МПа
bf g wf R wf = 1,1× 1×240 = 264 МПа
2. Расчет по металлу границы сплавления.
Коэффициент глубины провара шва bz =1,15 (СНиП II-23-81*, табл.34)
Коэффициент условия работы g wz = 1 (СНиП II-23-81*, пп. 11.2)
Расчетное сопротивление металла R wz =0,45 R un = 0,45 ×490 = 220,5 МПа
bz g wz R wz = 1,1× 1×220,5 = 253,6 МПа
Сравнивания полученные величины, находим
(b g w R w)min = 253,6 МПа
Высота катета поясного шва должна быть не менее
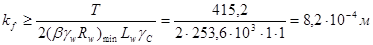
kf ≥ 0,8 мм
По толщине наиболее толстого из свариваемых элементов (tf = 18 мм) по табл. 38 СНиП II-23-81*, принимаем kf = 7 мм.
2.2.7. Проверка на устойчивость сжатой полки.
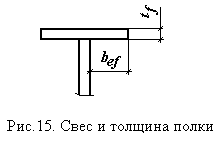
Устойчивость полки будет обеспечена, если отношение свеса полки bef к ее толщине tf не превышает предельного значения: 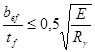 , где расчетная ширина свеса полки bef равна:
, где расчетная ширина свеса полки bef равна:

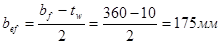

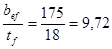


Т.к. 9,72 ‹ 12,8, устойчивость поясного листа обеспечена.
2.2.8. Проверка устойчивости стенки балки.
Для обеспечения устойчивости стенки вдоль пролета балки к стенке привариваются поперечные двусторонние ребра жесткости.
Расстояние между поперечными ребрами при условной гибкости стенки 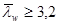 , не должно превышать 2hw. Условная гибкость стенки определяется по формуле
, не должно превышать 2hw. Условная гибкость стенки определяется по формуле
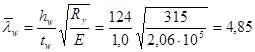 .
.
 При lw > 3,5 необходима проверка устойчивости стенки с установкой ребер жесткости с шагом не более 2hw = 2×124 = 248 см.
При lw > 3,5 необходима проверка устойчивости стенки с установкой ребер жесткости с шагом не более 2hw = 2×124 = 248 см.
Т.к. сопряжение балок выполняется в пониженном уровне, установку поперечных ребер предусматриваем с шагом 2,0 м.
Ширина ребер должна быть не менее
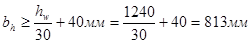
Принимаем bh = 100 мм.
Толщина ребра

Принимаем tS = 8 мм.
Проверка устойчивости стенки балки во втором отсеке в месте изменения сечения.
Критические нормальные напряжения
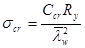 ;
;
По табл. 21, 22 СНиП II-23-81* определяем при d = ¥ и b = ¥, сcr = 35,5
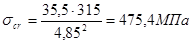
Критические касательные напряжения
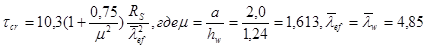
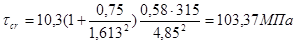
Нормальные и касательные напряжения в верхней фибре стенки
а) нормальные s = sх,а = 268,67 МПа;
б) касательные t = Q¢/(twhw) = 542, 46 ×10-3/(0,01×1,24) = 43,75 МПа.
Проверка устойчивости стенки
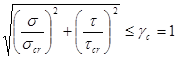 .
.
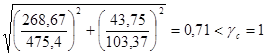
Проверка устойчивости стенки балки в первом отсеке (на расстоянии 125 см от опоры).
Изгибающий момент
М = RA × 1,25 = 817,58 кН × м.
Нормальные и касательные напряжения

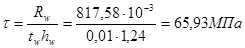
Проверка устойчивости стенки
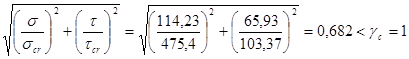
Проверка устойчивости удовлетворяется.
2.2.9. Расчет опорного ребра жесткости главной балки.
Принимаем сопряжение балки с колонной шарнирным, с опиранием на колонну сверху. Опорное ребро жесткости крепится сварными швами к стенке балки. Нижний торец опорного ребра балки остроган для непосредственной передачи давления на колонну.
Толщина опорного ребра определяется из расчета на смятие его торца
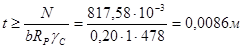 , где N = RA = 817,58 кН – опорная реакция;
, где N = RA = 817,58 кН – опорная реакция;
RP = Run/gm = 490/1,025 = 478 МПа – расчетное сопротивление стали смятию торцевой поверхности; b = b¢f = 20 см – ширина опорного ребра.
Принимаем толщину опорного ребра t = 10 мм, а опорный выступ а = 14 мм <1,5t = 1,5×10 = 15 мм.
Проверка ребра на устойчивость.
Площадь расчетного сечения ребра:
 ,
,
где 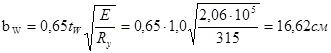 .
.
Радиус инерции сечения ребра 
Гибкость ребра  .
.
Условная гибкость 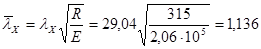 .
.
 Коэффициент продольного изгиба при lХ = 1,136
Коэффициент продольного изгиба при lХ = 1,136
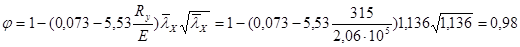 .
.
Проверка опорного ребра на устойчивость:
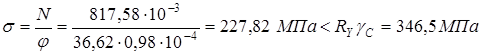
Расчет катета сварных швов крепления ребра к стенке балки:
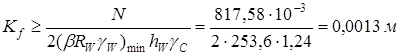
По толщине более толстого из свариваемых элементов принимаем катет шва Kf = 5 мм.
2.2.10. Расчет болтового соединения
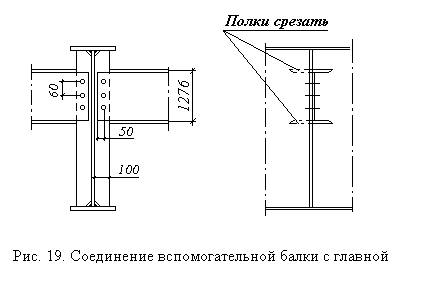
Сопряжение вспомогательной балки с главной выполняется поэтажно.
При пяти грузах в пролете опорная реакция вспомогательной балки равна
RA = 3,5 (G+P) = 3,5 × 33,248 = 116,4 кН
Принимаем болты нормальной точности (класс В), класс по прочности – 4,6, диаметром 20 мм. Расчетное сопротивление срезу болтов для принятого класса прочности Rbs = 150 Мпа.
Расчетные усилия, которые может выдержать один болт:
а) на срез
Nbs = Rbs × gb × A × ns,
где Rbs = 150 МПа,
gb = 0,9 – коэффициент условия работы,
ns = 1 – число срезов болта.
А = pd2/4 = 3,142×2,02/4 = 3,14 см2 – расчетная площадь сечения болта
Nbs = 150 × 103× 0,9 × 3,14 × 10-4 = 42,39 кН.
б) на смятие
Nb = Rbр × gb × d × S tmin,
где gb = 0,9;
Rbр = 690 МПа – расчетное сопротивление на смятие для стали при RUM = 490 МПа
S tmin = 10 мм – толщина стенки балки и ребра.
Nb = 690 × 103× 0,9 × 20 ×10-3× 10× 10-3 = 124,2 кН.
Сравнивая результаты, принимаем меньшее Nbs,min = 42,39 кН.
Требуемое количество болтов в соединении
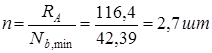
Принимаем 3 болта диаметром 20 мм, диаметр отверстия D=22 мм.
Проверка касательных напряжений в стенке вспомогательной балки с учетом ослабления отверстиями диаметром 22 мм под болты, а также с учетом ослабления сечения балки из-за вырезки полки в стыке, выполняется по формуле:

где Qmax = RA = 93,68 кН
hW = h – 2tf = 39,2 - 2×1,05 = 37,1
a = b/(b-d) = 146/(146 – 22) = 1,18 – коэффициент ослабления сечения
 |

Проверка удовлетворяется.