Министерство образования Российской Федерации
Волгоградский государственный архитектурно-строительный университет
Кафедра высшей математики
РЯДЫ
Методические указания и индивидуальные задания
К контрольной работе № 9
Волгоград 2004
УДК 517.537(076.5)
Ряды: Методические указания и индивидуальные задания к контрольной работе № 9 / Сост. Н.А. Болотина, К.В. Катеринин, И.П. Руденок; ВолгГАСА. Волгоград, 2004. — 12 c.
Содержатся краткие теоретические сведения и образцы решений типовых задач контрольной работы.
Для студентов 2-го курса института дистанционного обучения всех специальностей, кроме ЭУС, по дисциплине “Математика”.
Библиогр. назв. 3
План учеб.-метод. документ. 2003 г., поз. 10
Зав. редакцией О.Е. Горячева
Редактор Л.М. Ельцова
Компьютерная верстка К.В. Катеринин
Подписано в печать 12.05.04. Формат 60×84 1/16
Бумага офсетная. Печать трафаретная.
Гарнитура Таймс. Усл. печ. л. 0,7. Уч.-изд. л 0,75.
Тираж 300 экз. Заказ №
Волгоградский государственный архитектурно-строительный университет
Редакционно-издательский отдел
Сектор оперативной полиграфии ЦИТ
400074, Волгоград, ул. Академическая, 1
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
И РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
Числовые ряды. Основные понятия
Определение 1. Пусть дана бесконечная последовательность чисел  Выражение
Выражение
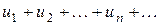 (1)
(1)
называется числовым рядом.
Выражение для n- го члена ряда называется общим членом ряда и обозначается  .
.
Коротко ряд записывается так:  .
.
Определение 2. Сумма конечного числа n первых членов ряда называется n- й частичной суммой ряда и обозначается 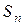 .
.
Определение 3. Если при  существует конечный предел
существует конечный предел  , то его называют суммой ряда и говорят, что ряд сходится.
, то его называют суммой ряда и говорят, что ряд сходится.
Если при  предел n- й частичной суммы не существует или он бесконечен, то говорят, что ряд расходится и суммы не имеет.
предел n- й частичной суммы не существует или он бесконечен, то говорят, что ряд расходится и суммы не имеет.
Необходимое условие сходимости ряда
Теорема. Если ряд (1) сходится, то при  его общий член стремится к нулю:
его общий член стремится к нулю:
 . (2)
. (2)
Замечание 1. Если для некоторого ряда  или этот предел не существует, то ряд расходится.
или этот предел не существует, то ряд расходится.
Замечание 2. При выполнении условия (2) исследуемый ряд может быть как сходящимся, так и расходящимся, и поэтому вопрос о сходимости ряда решается с помощью достаточных признаков сходимости.
Достаточные признаки сходимости и расходимости знакоположительных рядов
1. Признак Даламбера. Если  , то при
, то при 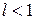 ряд сходится, при
ряд сходится, при  ряд расходится, при
ряд расходится, при  признак ответа не дает.
признак ответа не дает.
2. Признак Коши (радикальный). Если  , то при
, то при  ряд сходится, при
ряд сходится, при  ряд расходится, при
ряд расходится, при  признак ответа не дает.
признак ответа не дает.
3. Интегральный признак Коши. Пусть члены ряда  являются значениями непрерывной функции
являются значениями непрерывной функции  при целых значениях x и
при целых значениях x и  монотонно убывает на промежутке
монотонно убывает на промежутке  . Если несобственный интеграл
. Если несобственный интеграл 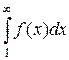 существует, то данный ряд сходится, если не существует, то ряд расходится.
существует, то данный ряд сходится, если не существует, то ряд расходится.
Признаки сравнения рядов.
Теорема 1. Пусть даны два знакоположительных ряда
 , (3)
, (3)
 , (4)
, (4)
и для любого n выполняется условие

В этом случае, если ряд (4) сходится, то ряд (3) также сходится. Если ряд (3) расходится, то расходится и ряд (4).
Теорема 2 (предельный признак сравнения). Если существует конечный и отличный от нуля предел  (то есть
(то есть  ), то ряды (2) и (3) одновременно сходятся или одновременно расходятся.
), то ряды (2) и (3) одновременно сходятся или одновременно расходятся.
Примечание. Приведенный теоретический материал используется для решения задач № 1—10 контрольной работы № 9.
Пример 1. Исследовать сходимость ряда  .
.
Решение.  то есть необходимый признак сходимости не выполняется, следовательно, ряд расходится.
то есть необходимый признак сходимости не выполняется, следовательно, ряд расходится.
Пример 2. Исследовать сходимость ряда  ,
,  .
.
Решение.  . По признаку Даламбера:
. По признаку Даламбера:
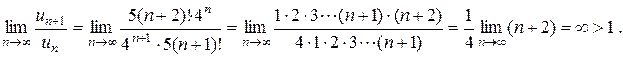 Ряд расходится.
Ряд расходится.
Пример 3. Исследовать сходимость числового ряда  .
.
Решение. По признаку Коши найдем
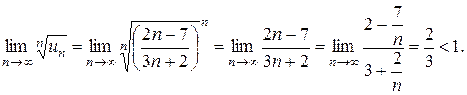 Ряд сходится.
Ряд сходится.
Пример 4.  ,
,  . Исследовать сходимость ряда
. Исследовать сходимость ряда  .
.
Решение. Применим интегральный признак Коши, положив  .
.
Эта функция удовлетворяет условиям теоремы Коши. Вычислим интеграл

Так как несобственный интеграл существует, то данный ряд сходится.
Пример 5. Исследовать сходимость ряда 
Решение. Сравним данный ряд с расходящимся гармоническим рядом  Пусть
Пусть  Так как
Так как 
то данный ряд так же, как и гармонический, расходится.
Знакочередующиеся ряды
Теорема Лейбница. Если члены знакочередующегося ряда
 ,
,
где  монотонно убывают по абсолютной величине и
монотонно убывают по абсолютной величине и 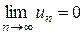 , то ряд сходится. Остаток ряда имеет знак своего первого члена и не превосходит его по абсолютной величине.
, то ряд сходится. Остаток ряда имеет знак своего первого члена и не превосходит его по абсолютной величине.
Достаточный признак сходимости знакопеременного ряда
Ряд называется знакопеременным, если среди его членов есть как положительные, так и отрицательные.
Теорема. Знакопеременный ряд  сходится, если сходится ряд, составленный из абсолютных величин его членов
сходится, если сходится ряд, составленный из абсолютных величин его членов
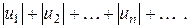 (5)
(5)
В этом случае исходный ряд называется абсолютно сходящимся.
Сходящийся знакопеременный ряд называется условно сходящимся, если ряд (5) расходится.
Степенные ряды
Если все коэффициенты степенного ряда
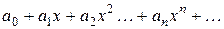
отличны от нуля, то радиус сходимости ряда можно найти по формулам:
 , (6)
, (6)
 . (7)
. (7)
В общем случае радиус сходимости степенного ряда находят, применяя признаки Даламбера или Коши непосредственно к ряду, не прибегая к формулам (6) и (7).
Интервал (– R; R) называется интервалом сходимости ряда. Множество точек, в которых ряд сходится, называется областью сходимости степенного ряда и обозначается X. Область сходимости или совпадает с интервалом сходимости, или включает его с одним или двумя концами.
Примечание. Приведенный теоретический материал используется при решении задач № 11—20 контрольной работы № 9.
Пример 6. Найти область сходимости степенного ряда  ,
, 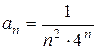 .
.
Решение. 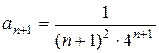 . Найдем радиус сходимости ряда по формуле (6):
. Найдем радиус сходимости ряда по формуле (6): 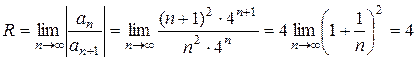 .
.
Интервал сходимости ряда (–4; 4). Исследуем сходимость ряда на концах интервала сходимости. При  получим ряд
получим ряд  , который сходится по признаку Лейбница. При
, который сходится по признаку Лейбница. При  получим ряд
получим ряд  , который сходится (это ряд обратных квадратов). Область сходимости данного ряда
, который сходится (это ряд обратных квадратов). Область сходимости данного ряда  .
.
Приближенное вычисление определенных интегралов
с помощью рядов
Для вычисления  сначала функцию
сначала функцию  разлагают в степенной ряд, а затем обе части полученного равенства интегрируют в пределах от 0 до b. При разложении функций в степенные ряды используют известные разложения:
разлагают в степенной ряд, а затем обе части полученного равенства интегрируют в пределах от 0 до b. При разложении функций в степенные ряды используют известные разложения:
e x 
 ,
,

 ,
,

 ,
,

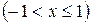 ,
,
arctg(x) 
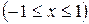 ,
,

Примечание. Приведенный теоретический материал используется при решении задач № 21—30 контрольной работы № 9.
Пример 7. Вычислить определенный интеграл  с точностью
с точностью
до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.
Решение. Разложим подынтегральную функцию в степенной ряд. Воспользуемся уже известным рядом:  . Заменив в нем
. Заменив в нем
x на  , получим
, получим 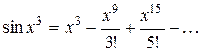 . Умножим обе части равенства на
. Умножим обе части равенства на  :
:  , отсюда
, отсюда

Замечаем, что третий член ряда по абсолютной величине меньше 0,001. Следовательно, для решения данной задачи, согласно признаку Лейбница, надо взять сумму первых двух членов, что обеспечит требуемую точность:
 .
.
Примечание. Ниже приведены образцы решения задач № 31—40 (пример 8) и № 41—50 (пример 9).
Интегрирование дифференциальных уравнений
с помощью рядов
Пример 8. Найти три первых, отличных от нуля, члена разложения в степенной ряд решения  дифференциального уравнения
дифференциального уравнения  , удовлетворяющего начальному условию
, удовлетворяющего начальному условию 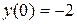 .
.
Решение. Представим решение данного уравнения в виде ряда
 . (8)
. (8)
Подставив начальное условие  ,
,  в (8), получим
в (8), получим  . Продифференцируем разложение (8):
. Продифференцируем разложение (8):
 . (9)
. (9)
Подставим в данное дифференциальное уравнение вместо  его значение (9), а вместо
его значение (9), а вместо  – его выражение (8), взяв первые три члена (в соответствии с условием задачи). Получим
– его выражение (8), взяв первые три члена (в соответствии с условием задачи). Получим  . Приравнивая коэффициенты при одинаковых степенях
. Приравнивая коэффициенты при одинаковых степенях  слева и справа последнего равенства, получим
слева и справа последнего равенства, получим  ,
,  . Так как
. Так как  , то
, то 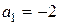 ,
, 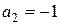 , и решение (8) примет вид
, и решение (8) примет вид  .
.
Разложение функций в ряды Фурье
Пример 9. Разложить функцию  в ряд Фурье в интервале
в ряд Фурье в интервале
(–π; π).
Решение. Данная функция ни четная, ни нечетная, поэтому её коэффициенты Фурье вычисляем по общим формулам:
 ,
,
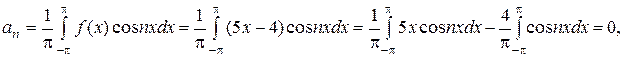

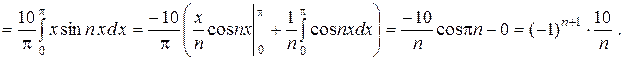
Подставив в ряд Фурье  найденные коэффициенты, получим:
найденные коэффициенты, получим:
 .
.
Пример 10. Разложить функцию  в ряд Фурье в интервале (–4; 4).
в ряд Фурье в интервале (–4; 4).
Решение. Данная функция является нечетной. Поэтому ее ряд Фурье будет иметь вид:
 где
где 
При  имеем:
имеем:  где
где  .
.
Для вычисления bn воспользуемся формулой интегрирования по частям, полагая u=x,  , получим
, получим

где  и окончательно получаем
и окончательно получаем
 для –4< x <4.
для –4< x <4.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
1—10. Исследовать сходимость числового ряда  .
.
1. 
 6.
6. 

2. 
 7.
7. 

3. 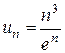 8.
8. 

4. 
 9.
9. 

5. 
 10.
10. 

11—20. Найти область сходимости степенного ряда  .
.
11.  16.
16. 
12.  17.
17. 
13. 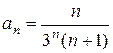 18.
18. 
14.  19.
19. 
15.  20.
20. 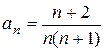
21—30. Вычислить определенный интеграл  с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.
21.  . 26.
. 26.  .
.
22.  . 27.
. 27.  .
.
23.  . 28.
. 28.  .
.
24. 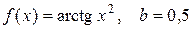 . 29.
. 29.  .
.
25.  . 30.
. 30.  .
.
31—40. Найти три первых, отличных от нуля, члена разложения в степенной ряд решения y = y (x) дифференциального уравнения 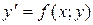 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию  .
.
31. 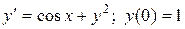 . 36.
. 36.  .
.
32. 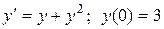 . 37.
. 37.  .
.
33.  . 38.
. 38.  .
.
34.  . 39.
. 39.  .
.
35.  . 40.
. 40.  .
.
41—50. Разложить данную функцию  в ряд Фурье в интервале (а; b).
в ряд Фурье в интервале (а; b).
41.  в интервале
в интервале  .
.
42.  в интервале
в интервале  .
.
43.  в интервале
в интервале  .
.
44.  в интервале
в интервале  .
.
45.  в интервале
в интервале  .
.
46.  в интервале
в интервале  .
.
47.  в интервале
в интервале  .
.
48. 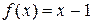 в интервале
в интервале  .
.
49.  в интервале
в интервале  .
.
50.  в интервале
в интервале  .
.
Библиографический список.
1. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т. 2. М.: Наука, 1978. — 576 с.
2. Шипачев В.С. Высшая математика. М.: Высшая школа, 1985. — 471 с.
3. Данко П.Е. Высшая математика в упражнениях и задачах. Ч. 2 / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. М.: Высшая школа, 1986. — 415 с.