Портфель из трёх бумаг А, В и С

Раздаточный материал

по теме 8 «Теория портфельного инвестирования»

Ожидаемая доходность портфеля определяется как средневзвешенная ожидаемая доходность входящих в него активов, а именно: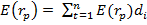

где: Е(r_p) — ожидаемая доходность портфеля;

Е(r₁); … Е(r_n) — ожидаемая доходность соответственно первого, второго и n -го активов;

d₁; d₂; d_n – удельный вес в портфеле первого, второго и n -го активов.

Удельный вес актива в портфеле рассчитывается как отношение его стоимости к стоимости всего портфеля или: d_i =

где: di – удельный вес i -го актива; P_i – стоимость i -го актива;

Р_p – стоимость портфеля.

Сумма всех удельных весов, входящих в портфель активов, всегда равна единице.

Пример 8.1.

Портфель состоит из двух активов А и В. Е(r_a) = 15%, Е(r_B) = 10%.

Стоимость актива А – 300 тыс. руб., актива В – 700 тыс. руб. Необходимо определить ожидаемую доходность портфеля.

Стоимость портфеля равна: 300 тыс.+ 700 тыс. =1000 тыс. руб.

Удельные веса активов равны: d₁ = d₂ =

Для определения ожидаемой доходности портфеля на основе ожидаемой доходности активов воспользуемся формулой:

Ответ: доходность портфеля составит 11,5%..

Ожидаемый риск актива и портфеля

Дисперсия определяется по формуле

где: σ² – дисперсия доходности актива; n – число периодов наблюдения;

– средняя доходность актива.

Стандартное отклонение определяется как квадратный корень из дисперсии

σ =

где: σ— стандартное отклонение доходности актива.

Пример 8.2. Данные о доходности активов А и В приведены в таблице (табл.8.2).

 

Таблица 8.1. Доходность бумаг А и В (в %)

Год
		–4,25	18,0625		–2,75	7,5625
		1,75	3,0625		3,25	10,5625
		–0,25	0,0625		–0,75	0,5625
		2,75	7,5625		0,25	0,0625
∑			28,75			18,75
Среднее	14,25			14,75
Дисперсия			7,19			4,69
Станд.откл.			2,68			2,17

Показатель ковариации определяется по формуле

=

где: ковариация доходности активов А и В;

_A — средняя доходность актива А за n периодов;

_B — средняя доходность актива В за n периодов;

r_A – доходность актива А в i-м периоде;

r_B – доходность актива В в i-м периоде;

п – число периодов, за которые регистрировалась доходность активов А и В.

Другим показателем степени взаимосвязи изменения доходностей двух активов служит коэффициент корреляции. Он рассчитывается по формуле

=

где: Соrr_A,B – коэффициент корреляции доходности активов А и В;

Сov _A,B – ковариация доходности активов А и В;

σ_A – стандартное отклонение доходности актива А;

σ_B – стандартное отклонение доходности актива В.

 

Таблица 8.2. Расчёт коэффициентов ковариации и корреляции бумаг А и В

Год	–	–	– ( –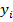
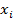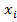	–4,25	–2,75	11,6875
	1,75	3,25	5,6875
	–0,25	–0,75	0,1875
	2,75	0,25	0,6875
∑			18,25

 

Так как в нашем примере небольшое количество наблюдений, то в знаменателе

вместо п – 1 берём значение п.

Коэффициент ковариации =

Коэффициент корреляции =

Пример 8.3

Определить доли бумаг А и Вв портфеле с минимальным риском если:

= 7,19;

Удельные веса активов составят:

и = 0,953.

Ответ: портфель с минимальным риском должен содержать 4,7% бумаг А и 95,3% бумаг В.

Портфель из бумаг А и С

Таблица 8.3. Расчёт ковариации и корреляции доходности бумаг А и С

Год	Бумага А (%)	Бумага С (%)	(
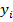
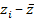
		–4,25	18,0625
		1,75	3,0625
		–0,25	0,0625
		2,75	7,5625
Сумма			28,75
Среднее	14,25
Дисперсия			7,19
Станд.откл.			2,68
Ковариация

(Так как в нашем примере небольшое количество наблюдений, то в знаменателе вместо п – 1 берём значение п).

= =

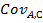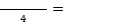
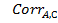Пример 8.4

Определить доли бумаг А и Св портфеле с минимальным риском если:

=; Удельные веса активов составят:

и =

Ответ: портфель с минимальным риском должен содержать % бумаг А и % бумаг С.

Портфель из бумаг В и С

Таблица 8.4. Расчёт ковариации и корреляции доходности бумаг В и С

Год	Бумага В (%)	Бумага С (%)	(
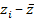
Сумма
Среднее
Дисперсия
Станд.откл.
Ковариация

(Так как в нашем примере небольшое количество наблюдений, то в знаменателе вместо п – 1 берём значение п).

= =

Пример 8.5

Определить доли бумаг В и Св портфеле с минимальным риском если:

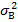=; Удельные веса активов составят:

и =

Ответ: портфель с минимальным риском должен содержать % бумаг В и % бумаг С.

 

Портфель из трёх бумаг А, В и С

По результатам расчётов составим сводные таблицы характеристик бумаг, ковариаций и корреляций.

Таблица 8.4 Характеристики бумаг

Показатель	А	В	С
Средняя доходность, %
Дисперсия доходности
Стандартное отклонение

 

Таблица 8.5 Матрица ковариаций Таблица 8.6 Матрица корреляций

	А	В	С			А	В	С
А				А
В				В
С				С

 

Зададим доли каждой бумаги в портфеле: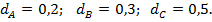

Ожидаемая доходность портфеля (ОДП) составит:

ОДП = _________________________________________________________________%.

Таблица 8.7 Расчёт дисперсии и стандартного отклонения портфеля

АА
АВ
АС		Сумма
ВА
ВВ
ВС		Сумма
СА
СВ
СС		Сумма
	Сумма сумм

 

Дисперсия портфеля Стандартное отклонение =