Убедиться в том, что опыты воспроизводимы, т. е. результаты опытов, проведенных в одинаковых условиях, близки друг к другу. Для этой цели проводят несколько серий параллельных опытов. Условия реализации опытов каждой серии — одинаковы, а разных серий — отличаются друг от друга. Однако все опыты проводятся в рассматриваемой области изменения влияющих факторов. Результаты этих опытов сводят в таблицу табл. 10. Количество опытов во всех сериях должно быть одинаковым.
Для каждой серии параллельных опытов вычисляют среднее арифметическое значение функции отклика
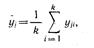
где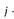 
— номер серии; 
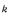— число параллельных опытов, проведенных при одинаковых условиях.
Затем вычисляют для каждой серии параллельных опытов величину, называемую оценкой дисперсии:
Среди всех оценок дисперсий находят наибольшую. Мы обозначим ее через 
аблица 10 Эксперимент для проверки воспроизводимости опытов
| Номер серии опытов | Результаты параллельных опытов | Средние значения | Оценки дисперсии |
|
Затем находят отношение наибольшей из оценок дисперсий к сумме всех оценок дисперсий:
Таблица11 Критические значения критерия Кохрена
| Число серий опытов (число оценок дисперсий) | 
| |||
| 0,999 | 0,975 | 0,939 | 0,906 | |
| 0,967 | 0,871 | 0,798 | 0,746 | |
| 0,907 | 0,768 | 0,684 | 0,629 | |
| 0,841 | 0,684 | 0,598 | 0,544 |
Величина Gp называется расчетным значением критерия Кохрена. Критические, т. е. предельно допустимые значения критерия Кохрена G, приведены в табл. 11.
Для нахождения G необходимо знать общее число N оценок дисперсий и так называемое число степеней свободы 
, связанных с каждой из них, причем
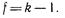
Опыты считаются воспроизводимыми, когда выполняется условие
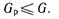
Если опыты невоспроизводимы, то можно попытаться достигнуть воспроизводимости путем выявления и устранения источников нестабильности эксперимента, а также за счет использования более точных измерительных приборов.
Наконец, если никакими способами невозможно обеспечить воспроизводимость, то математические методы планирования к такому эксперименту применять нельзя.
Если при проведении эксперимента опыты дублируют и пользуются средними значениями функции отклика 
то при обработке экспериментальных данных следует использовать 
В тех случаях, когда из-за недостатка времени, большой трудоемкости или высокой стоимости эксперимента опыты не дублируют, при обработке экспериментальных данных используют 
Таким образом, вычисления, связанные с проверкой воспроизводимости опытов, достаточно просты. Для их проведения достаточно использовать микрокалькулятор.
Полный факторный эксперимент
Под математическим описанием технологического процесса обычно понимают систему уравнений, связывающих функции отклика с влияющими факторами. В простейшем случае это может быть одно уравнение. Часто математическое описание называют математической моделью.
С помощью математических методов планирования эксперимента можно получить математическую модель технологического процесса даже при отсутствии сведений о механизме его протекания. Это в ряде случаев бывает очень полезно.
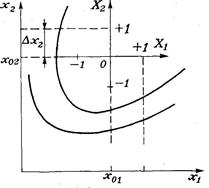
Рис. 21 Введение кодированных переменных
На основе планирования эксперимента возможно моделировать химический состав продукта, его выход, усвояемость и др. показатели качества продукта или правильным термином «факторы».
Математические модели, получаемые с помощью методов планирования эксперимента, принято называть экспериментально-статистическими.
Метод полного факторного эксперимента дает возможность получить математическое описание пищевого технологического процесса в некоторой области факторного пространства, лежащей в окрестности выбранной точки с координатами 
где 
- число факторов).
Перенесем начало координат факторного пространства в данную точку рис. 21. С этой целью введем новые переменные величины
где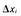 
— выбранный нами масштаб по оси 
Величины 
не имеют размерностей и называются кодированными переменными.
С помощью полного факторного эксперимента ищут математическое описание технологического процесса в виде уравнения
В него входит свободный член 
члены в виде произведений коэффициентов регрессии 
на 
и члены, содержащие парные произведения кодированных переменных. Таким образом, это — неполное квадратное уравнение.
Все факторы в ходе полного факторного эксперимента варьируют на двух уровнях, соответствующих значениям кодированных переменных 
и 
.
В табл. 13 приведены условия опытов полного двухфакторного эксперимента. Часть таблицы, обведенная штриховыми линиями, называется матрицей планирования.
Таблица 13 Условия полного двухфакторного эксперимента
| Номер опыта | Факторы | Функция отклика | |
 X1
| X2 | ||
| -1 | -1 | y1 | |
| +1 | -1 | y2 | |
| -1 | +1 | y3 | |
| +1 | +1 | y4 |
Матрица содержит полный набор всех возможных комбинаций уровней варьирования факторов. Отсюда полный факторный эксперимент получил свое название.
Как следует из рис. 22, результаты опытов, приведенные в табл. 13, соответствуют на факторной плоскости вершинам квадрата с центром в начале координат.
Рис. 22. Полной двухфакторной эксперимент на плоскости
В табл. 14 приведены условия опытов полного трехфакторного эксперимента. Эти опыты соответствуют в факторном пространстве вершинам куба с центром в начале координат.
Основные принципы построения матриц планирования полного факторного эксперимента: 1) уровни варьирования первого фактора чередуются от опыта к опыту; 2) частота смены уровней варьирования каждого последующего фактора вдвое меньше, чем у предыдущего.
Таблица 13 Условия полного трехфакторного эксперимента
| Номер опыта | Факторы | Функция отклика | ||
| X1 | X2 | X3 | ||
| 1. | - 1 | - 1 | -1 | y1 |
| 2. | + 1 | - 1 | - 1 | y2 |
| 3. | - 1 | + 1 | - 1 | y3 |
| 4. | + 1 | + 1 | - 1 | y4 |
| 5. | - 1 | - 1 | + 1 | y5 |
| 6. | + 1 | -1 | + 1 | y6 |
| 7. | - 1 | + 1 | + 1 | y7 |
| 8. | + 1 | + 1 | + 1 | y8 |
Общее число опытов полного факторного эксперимента:
где n — число факторов.
На основании результатов полного факторного эксперимента вычисляют коэффициенты регрессии, пользуясь следующими формулами:
Некоторые из коэффициентов регрессии могут оказаться пренебрежимо малыми - незначимыми. Чтобы установить, значим коэффициент или нет, необходимо прежде всего вычислить оценку дисперсии, с которой он определяется:
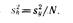
Следует отметить, что по результатам полного факторного эксперимента все коэффициенты определяются с одинаковой погрешностью.
Принято считать, что коэффициент регрессии значим, если выполнено условие
где 
— значение критерия Стьюдента, взятое из табл. 15.
Для пользования табл. 15 необходимо знать число степеней свободы 
связанное с оценкой дисперсии 
Таблица 15 Значения критерия Стьюдента
| f | t |
| 12,71 | |
| 4,30 | |
| 3,18 | |
| 2,78 | |
| 2,57 | |
| 2.45 | |
| 2,36 | |
| 2,31 | |
| 2,26 | |
| 2,23 |
Если проверка показала, что коэффициент регрессии незначим, то соответствующий член можно исключить из уравнения.
Получив уравнение регрессии, следует проверить его адекватность, то есть способность достаточно хорошо описывать поверхность отклика и прогнозировать результаты опытов. Для проверки адекватности вычисляют оценку дисперсии адекватности по формуле
Здесь 
— число значимых коэффициентов регрессии; 
— экспериментальное и расчетное значение функции отклика в 
опыте; 
— число опытов полного факторного эксперимента.
С оценкой дисперсии адекватности связано число степеней свободы
Затем находят расчетное значение критерия Фишера:
Уравнение регрессии считается адекватным, если выполняется условие
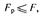
где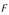 
— критическое значение критерия Фишера табл. 16.
Для пользования табл. 19 необходимо знать числа степеней свободы, связанных с числителем и знаменателем отношения 