Методом дробного факторного эксперимента

 

С увеличением числа учитываемых факторов резко возрастает число опытов полного факторного эксперимента.

Для нахождения коэффициентов регрессии не всегда требуется много опытов. В таких случаях можно уменьшить объем экспериментальных работ, воспользовавшись методом дробного факторного эксперимента, который известен также под названием метода дробных реплик.

Этот метод заключается в том, что для нахождения уравнения регрессии используется определенная часть полного факторного эксперимента: и т. д. Такие системы опытов называются дробными репликами табл. 19.

 

Таблица 19

Полный трехфакторный эксперимент и его дробные реплики

 

Расчет коэффициентов регрессии, проверка значимости коэффициентов и адекватности математического описания в данном случае осуществляются так же, как и при полном факторном эксперименте.

Пусть требуется найти коэффициенты уравнения регрессии

 

 

Если для этой цели воспользоваться полным трехфакторным экспериментом, то необходимо провести 8 опытов. Однако эту задачу можно решить и с помощью меньшего числа опытов. Например, возьмем матрицу полного двухфакторного эксперимента табл. 20 и приравняем произведение 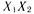к фактору

Рассчитаем коэффициенты регрессии:

 

 

Обратим внимание на то, что в табл. 20 столбцы для произведения и фактора 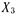полностью совпадают. Поэтому коэффициенты регресси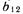и и 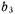не могут быть определены раздельно.

Таблица 20 Дробный факторный эксперимент типа 2^3-1

Номер опыта	X1	X2	X1X2	X3	Функция отклика
	- 1	- 1	+ 1	+ 1	y1
	+ 1	- 1	- 1	- 1	y2
	- 1	+ 1	-1	- 1	y3
	+ 1	+ 1	+ 1	+ 1	y4

 

Может быть найдена только их сумма:

 

 

Этот недостаток рассматриваемого плана является своеобразной «платой» за уменьшение общего числа опытов с восьми до четырех.

Такое планирование эксперимента, когда некоторые из факторов приравнивают к произведениям нескольких факторов, называется планированием со смешиванием. Его обозначают символом где — общее число факторов, а 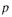— число факторов, приравненных к произведениям. С этой точки зрения в табл. 20 приведена матрица планирования типа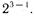

Существует правило, позволяющее определить, какие коэффициенты регрессии определяются совместно при планировании со смешиванием. Рассмотрим это правило на примере.

Методом дробных реплик будем искать математическое описание процесса в виде уравнения регрессии

 

 

Воспользуемся планированием типа и примем

 

Такие равенства в методе дробных реплик называются генерирующими соотношениями.

Следует отметить, что выбор генерирующих соотношений в общем случае произволен. Однако он существенно влияет на характер совместных оценок коэффициентов регрессии.

Правило определения совместных оценок коэффициентов заключается в следующем:

Примем во внимание, что

 

 

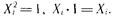
Умножив обе части генерирующих соотношений соответственно на 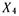и получим:

 

 

Эти равенства называются определяющими контрастами. Перемножив их почленно, получим новые определяющие контрасты.

В данном случае _

 

 

3. Составим алгебраическую сумму из единицы и правых частей всех полученных определяющих контрастов:

 

 

4. Умножив каждый из факторов на s и заменив факторы соответствующими коэффициентами регрессии р получим искомые совместные оценки:

 

где 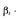— истинные коэффициенты регрессии.

В рассмотренном примере удалось значительно сократить общее количество опытов. Так, полный пятифакторный эксперимент состоит из 32 опытов. План типа содержит 8 опытов, т. е. в четыре раза меньше.

Отметим еще одну интересную особенность дробного факторного эксперимента. Планирование со смешиванием иногда применяют в тех случаях, когда необходимо уменьшить влияние неуправляемых временных изменений некоторых влияющих факторов, т. е. влияние так называемого временного дрейфа. Примером временного дрейфа может служить уменьшение со временем активности катализатора вследствие отравления его каталитическими ядами.

При постановке большой серии опытов, требующих длительного времени, всегда приходится опасаться нежелательных изменений исходных свойств реагентов, некоторых характеристик технологического оборудования и т. п. Влияние этого временного дрейфа на параметры математического описания процесса можно практически устранить, разбивая всю серию опытов на отдельные блоки так, чтобы эффект от временного дрейфа оказался смешанным с произведениями факторов, для которых коэффициенты регрессии достаточно малы.

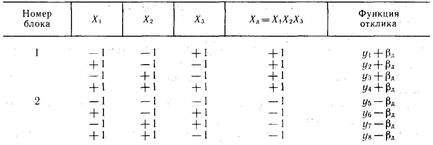
Допустим, что необходимо устранить влияние временного дрейфа на параметры уравнения регрессии, получаемого в результате полного трехфакторного эксперимента. С этой целью разобъем эксперимент на два блока и введем новую независимую переменную Х_Л, характеризующую дрейф. Положим

 

Исходя из матрицы планирования, представленной в табл. 21, будем считать, что в первом блоке все результаты опытов вследствие временного дрейфа завышены на а во втором — занижены на ту же величину.

 

Таблица 21 Планирование в условиях временного дрейфа

 

Если уравнение регрессии отыскивается в виде

 

 

то коэффициенты регрессии будут являться следующими оценками:

 

 

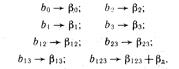
Рассчитаем, например, коэффициенты и :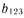

 

 

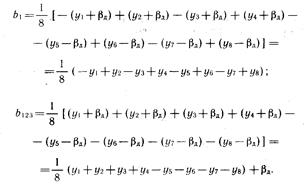
Следовательно, все коэффициенты регрессии, кроме не содержат погрешностей, обусловленных временным дрейфом.

 

Крутое восхождение

 

Полученное с помощью полного или дробного факторного эксперимента уравнение регрессии служит не только математической моделью химико-технологического процесса, но используется и для его оптимизации. Оптимизацией процесса называют целенаправленный поиск наилучших в определенном смысле условий его проведения. Задачи оптимизации приходится решать при разработке новых технологий и реконструкции действующих производств.

Величина, характеризующая уровень оптимизации процесса, называется критерием оптимальности или целевой функцией. Например, критерием оптимальности может быть выход целевого продукта химической реакции в расчете на израсходованное сырье.

Качество процесса химической технологии обычно выражается не одним, а несколькими показателями. Безусловно, хочется, чтобы все показатели достигали одновременно своих наилучших значений. К сожалению, это невозможно. Например, максимальная производительность оборудования и минимальная себестоимость продукции обычно имеют место при различных технологических режимах.

Чтобы осуществлять оптимизацию, необходимо располагать определенными ресурсами. Например, для увеличения выхода целевого продукта химической реакции, мы должны иметь возможность варьировать в определенных пределах значениями таких величин, как температура реакционной-смеси, исходные концентрации реагентов и т. д.

Оптимизацию проводят, как правило, в условиях ограничений на ресурсы оптимизации и некоторые выходные параметры процесса.

Задачу оптимизации можно сформулировать следующим образом. Задан критерий оптимальности

 

и ограничения на остальные выходные параметры процесса:

 

 

Заданы ограничения на ресурсы оптимизации:

 

 

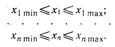
Требуется найти такие значения ресурсов оптимизации при которых критерий оптимальности достигает своего экстремального (т. е. наибольшего или наименьшего) значения.

Д. Бокс и К. Уилсон предложили использовать для оптимизации результаты полного или дробного факторного эксперимента. Сущность этого метода состоит в следующем.

Среди всех имеющихся функций отклика, описывающих объект оптимизации, выбирают одну наиболее важную и принимают ее в качестве критерия оптимальности Затем указывают ограничения, накладываемые на остальные функции отклика и на влияющие факторы.

Один из наиболее сильно влияющих факторов принимают за базовый и для него вычисляют произведение соответствующего коэффициента регрессии на шаг варьирования. Например, для первого фактора это произведение имеет вид Затем для базового фактора выбирают шаг с которым будет осуществляться оптимизация. С целью более точного нахождения координат оптимума обычно принимают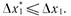

После этого вычисляют отношение

 

Для всех остальных факторов шаги движения к оптимуму рассчитывают по формуле

 

 

Движение к оптимуму начинают из центра плана, который был использован для получения уравнения регрессии. Значения факторов на каждом новом шаге оптимизации находят путем прибавления к соответствующим предыдущим значениям. Так осуществляется оптимизация по методу Бокса и Уилсона, получившему название метода крутого восхождения. Отметим некоторые особенности этого метода. Движение из центра плана начинается в сторону наиболее быстрого увеличения критерия оптимальности. Это происходит благодаря тому, что шаги пропорциональны коэффициентам регрессии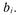

Если ищется минимум критерия 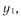то новые значения факторов 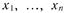находят из предыдущих путем вычитания Такой способ оптимизации назван методом наискорейшего спуска.

Движение к экстремуму прекращают при выполнении следующих условий: 1) значения факторов 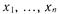(одного или нескольких) или функций отклика (одной или нескольких) вышли на допустимые границы; 2) достигнут экстремум критерия оптимальности.

 

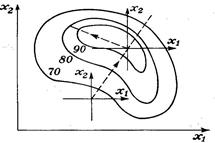
Рис. 23. Оптимизация по методу крутого восхождения

Как следует из рис. 23, в ходе крутого восхождения по поверхности отклика сначала может быть достигнут локальный экстремум на направлении движения. В таком случае необходимо в окрестности этого экстремума поставить новый полный факторный эксперимент и реализовать новое крутое восхождение.

Отметим, что в реальных условиях оптимум обычно находится на границах области допустимых значений