Государственный таможенный комитет Российской Федерации
Российская таможенная академия
Статистика
Задача 1. Выполнить аналитическую группировки статистических данных
Методом аналитической группировки устанавливается наличие связи между среднегодовой стоимостью основных фондов (факторный признак) и стоимостью продукции (результативный признак). Группировка производится по факторному признаку. Выделенные группы затем необходимо охарактеризовать приведенными в условие задачи показателями.
На первом этапе строится макет групповой аналитической таблицы.
На втором этапе находится интервал группировки по среднегодовой стоимости основных производственных фондов и формируются группы предприятий по факторному признаку. Для заполнения макета аналитической таблицы строится рабочая таблица. Данные рабочей таблицы переносятся в макет построенной таблицы и оформляется результат группировки в виде групповой аналитической таблицы. Таблицы должны иметь заглавие, наименование подлежащего и сказуемого таблицы, единицы измерения, расчетные показатели и т.д.
После построения групповой аналитической таблицы необходимо сделать выводы.
Задача 2. Выполнить расчет средней арифметической и средней гармонической взвешенной. Вид средней вычисляется на основе исходной статистической информации и выбора соответствующей формулы для средней арифметической взвешенной:
где: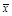 
- средняя величина; х – индивидуальное значение осредняемого признака; f - число повторений признака;
для средней гармонической взвешенной:
где: М = x · f.
Задача 3. Предполагает расчет аналитических показателей динамических рядов. В условии задачи дан интервальный динамический ряд, поэтому средний уровень ряда может быть исчислен только по формуле средней арифметической простой:
|
|
,
т.е. средний уровень ряда равен сумме уровней ряда, деленной на их число.
В зависимости от задачи исследования абсолютные приросты (снижение - 
-), темпы роста (снижение - Т) и темпы прироста (снижение - ТD), могут быть рассчитаны с переменной базой сравнения (ценные) и постоянной базой сравнения (базисные).
Абсолютные приросты:
цепные -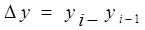 
,
базисные - 
.
Средний абсолютный прирост исчисляется двумя способами:
а) как средняя арифметическая простая цепных приростов:
;
б) делением базисного прироста на число периодов (лет, месяцев и т.д.)
.
Темпы прироста:
цепные - 
,
базисные -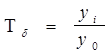 
.
Среднегодовой темп роста исчисляется по формуле средней геометрической двумя способами:
1. 
, или 
где: Т - цепные коэффициенты роста; n - число коэффициентов; П - знак произведения;
ПТ - произведение цепных коэффициентов роста за полученный период.
,
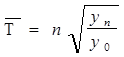где: 
- начальный уровень; 
- конечный уровень;
n - число уровней ряда динамики в изучаемом периоде, не считая базисного.
Задача 4. Предполагает расчет среднего уровня моментного ряда динамики с равными интервалами. Определяется по формуле - средней хронологической:
,
где:
n - число уровней ряда динамики.
Задача 5. Предполагает расчет:
1) агрегатных индексов количественных показателей:
а) общий индекс затрат на производство продукции:
;
б) общий индекс себестоимости продукции
|
|
в) общий индекс физического объема производства продукции
;
Необходимо уяснить правило выбора веса для качественных (себестоимость, урожайность, цена и т.д.) и количественных (количество произведенной, проданной продукции и т.д.) признаков при построении агрегатных форм общих индексов.
1) расчет индексов качественных показателей: индекса переменного состава, индекса постоянного состава и индекса, измеряющего влияние изменения структуры на динамику среднего показателя (индексы структурных сдвигов).
Индекс переменного состава равен соотношению средних уровней изучаемого признака. Если, например, изучается динамика себестоимости одноименной продукции на двух и более заводах, то индекс себестоимости переменного состава исчисляется по формуле:
Изменение средней себестоимости единицы продукции может быть обусловлено изменением себестоимости единицы продукции на каждом заводе и изменением удельного веса производства продукции на заводах.
Выявление влияния каждого из факторов на динамику средней себестоимости продукции можно осуществить при помощи расчета индекса себестоимости постоянного состава и индекса структурных сдвигов. Индекс себестоимости постоянного (фиксированного) состава или индекс себестоимости в постоянной структуре:
Этот индекс характеризует изменение средней себестоимости единицы продукции за счет изменения только себестоимости на каждом заводе.
Индекс структурных сдвигов:
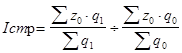
Этот индекс характеризует изменение средней себестоимости единицы продукции за счет изменения только удельного веса количества произведенной продукции на заводах.
|
|
Индекс структурных сдвигов можно исчислить, используя взаимосвязь индексов: 
.
Задача 6. Предполагает расчет среднеарифметического или среднегармонического индексов. Практическое их применение зависит от исходной статистической информации. Агрегатный индекс может быть преобразован в среднеарифметический или в среднегармонический индекс, при этом должно быть соблюдено тождество между индексами. Если у исходного агрегатного индекса реальная величина в числителе, то преобразуем в среднеарифметическую форму. Например, индекс цен:
.
В числителе индекса - фактический товарооборот отчетного периода. Заменив 
его значением из индивидуального индекса,
, получим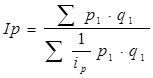 
.
Это и есть среднегармонический индекс цен. Преобразование агрегатного индекса цен в среднеарифметическую форму нецелесообразно - практического применения нет.
Агрегатный индекс физического объема товарооборота 
исходя из правила будет преобразован в среднеарифметический индекс, т.е.
.