Физика, 11 класс – САРАХМАН АЛИНА
Тема урока: ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ.САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ.
Цель урока: Дать понятие об энергетической характеристике индукционного электрического тока, возникающего в движущихся проводниках.
Работу выполнить в рабочей тетради, не забыв подписать вверху каждого листа фамилию и имя; выполненные задания прислать после урока по расписанию на мою страничку ВКОНТАКТЕ личным сообщением или на почтуgarmatenko_marina_22@mail.ru
Ход урока
ЗАПИСЫВАЕМ В ТЕТРАДИ:
Число: 10ноября
Тема урока: ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ.САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ.
РАБОТА НАД НОВОЙ ТЕМОЙ:
- п.9 - 11 – самостоятельное чтение
- Записать: (можно сократить запись, основное выписать)
- ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром 
- Индукционный ток в неподвижном замкнутом контуре, находящемся в переменном магнитном поле, вызывается электрическим полем, порождаемым переменным магнитным полем, которое называется вихревым.
- Работа вихревого электрического поля при перемещении единичного положительного заряда вдоль замкнутого неподвижного проводника численно равна ЭДС индукции в этом проводнике.
Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле.
Пусть сторона контура MN длиной l скользит с постоянной скоростью υ вдоль сторон NC и MD, оставаясь все время параллельной стороне CD. Вектор магнитной индукции 
однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.
Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю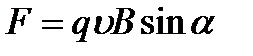 
Направлена она вдоль проводника MN.
Работа данной силы на пути l положительна и равна 
.
ЭДС индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду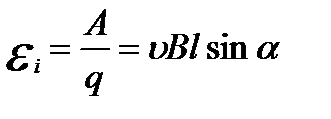 
.
С другой стороны, ЭДС индукции можно вычислить с помощью закона эл/м индукции.
Изменениемагнитного потока за это время равно 
.
Следовательно,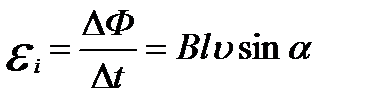 
Самоиндукция – это явление возникновения электромагнитной индукции в проводнике при изменении силы тока, протекающего сквозь этот проводник.
Индуктивность. Модуль вектора индукции В магнитного поля, создаваемого током, пропорционален силе тока. Так как магнитный поток Ф пропорционален В, то Ф ~ В~ I.
Можно, следовательно, утверждать, чтоФ = LI, где L — коэффициент пропорциональности между током в проводящем контуре и магнитным потоком.
Величину L называют индуктивностью контура, или его коэффициентом самоиндукции.
Используя закон электромагнитной индукции и полученное выражение, получаем равенство
Единицу индуктивности в СИ называют генри (обозначается Гн).
Энергия магнитного поля тока.
РЕШИТЬ ЗАДАЧИ:
1.Найти ЭДС индукции в проводнике с длиной активной части 25 см, перемещающемся в однородном магнитном поле индукцией 8мТл со скоростью 5 м/с под углом 60° к вектору магнитной индукции. (0,005 В)
2.С какой скоростью надо перемещать проводник, длина активной части которого 1 м, под углом 30° к линиям индукции магнитного поля, чтобы в проводнике возбуждалась ЭДС индукции 1В? Индукция магнитного поля равна 0,2 Тл. (5,8 м/с)
3. Прямолинейный проводник длиной 0,5м движется в магнитном поле со скоростью 6 м/с под углом 300 к вектору индукции. Определить индукцию магнитного поля, если в проводнике возникает ЭДС индукции 3 В.
4. Катушка сопротивлением 100 Ом, состоящая из 1000 витков площадью 5 см2, внесена в однородное магнитное поле. В течение некоторого времени индукция магнитного поля уменьшилась от 0,8 до 0,3 Тл. Какой заряд индуцирован в проводнике за это время?
№931. Какова индуктивность контура, если при силе тока 5 А в нем возникает магнитный поток 0,5 мВб?
Советую посмотреть видео по ссылке:
https://www.youtube.com/watch?v=W7bHysLJt5Y&t=10s
https://www.youtube.com/watch?v=V9XtThjVhi4