Представление двоичных чисел в компьютере в силу особенностей аппаратной реализации современных компьютеров (использование регистров для хранения информации) отличается от записи чисел в привычной для нас форме представления. Выполнение арифметических операций в компьютере также отличается от операций над двоичными числами при использовании обычной двоичной арифметики. Поэтому можно говорить о так называемой «компьютерной» арифметике, отличительными чертами которой являются:
· использование вместо двоичных чисел цепочек цифр (нулей и единиц). Напомним, что число отличается от цепочки цифр тем, что первая (старшая) его цифра не может быть нулем, в цепочках же цифр это возможно;
· строго фиксированное число цифр в цепочке, определяемое числом разрядов в регистрах (8, 16, 32, 64) в зависимости от типа компьютера. Число цифр в цепочке не зависит от значения представляемого числа или указателя, недостающие слева цифры заполняются нулями. Так, например, двоичное число 112=310 будет представляться в компьютерной арифметике в виде 00000011 при использовании восьмиразрядных регистров и 0000000000000011 при использовании шестнадцатиразрядных регистров.
· использование в качестве базовых операций только двух операций: операции сложения и операции сдвига. При этом в компьютере арифметические операции выполняются не над двоичными числами по правилам двоичной арифметики, а над кодами (цепочками) двоичных чисел фиксированной длины по правилам компьютерной арифметики;
· разделение по смыслу цепочек цифр на цепочки, представляющий собой числа в обычном понимании этого слова и цепочки, представляющие собой указатели, используемые для обозначения адресов, команд и данных.
Особенностью компьютерной арифметики является то, что для представления целых чисел без знака и со знаком, а также вещественных чисел существуют специфические формы представления в компьютере. Напомним, что само выполнение арифметических операций в компьютерной арифметике производится по особым правилам, отличным от правил традиционной двоичной арифметики.
Рассмотрим различные формы представления двоичных чисел в компьютере и особенности выполнения арифметических операций над ними в компьютерной арифметике.
ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ БЕЗ ЗНАКА.
Простейшим типом данных, с которым оперирует компьютер, являются целые числа. Казалось бы, что мешает их рассматривать как вещественные числа с нулевой дробной частью? Тогда бы и любые вычисления сводились к арифметическим действиям над вещественными данными. Однако в целях повышения быстродействия и эффективного расходования памяти компьютера целые числа целесообразно представлять в специальных форматах. Для компьютерного представления целых чисел обычно используется несколько различных форматов, отличающихся друг от друга количеством разрядов и наличием или отсутствием знакового разряда. Чаще всего используется восьми-, шестнадцати- и тридцатидвухразрядная сетка для представления таких чисел.
Целое число без знака располагается в регистре (слове, полуслове или двойном слове) так, что его самый младший двоичный разряд записывается в крайний правый бит разрядной сетки, причем все разряды должны быть обязательно заполнены, даже если в этом разряде будет храниться «незначащий ноль». Условились нумеровать разряды регистров (битов) справа налево, начиная с нуля. Например, десятичное число 1910=100112 в 16-разрядном представлении (полуслове) запишется так:
При такой форме представления целых чисел без знака диапазон их возможных значений находится в пределах от 0 до 2n-1, где п – число разрядов в регистре (разрядной сетке). Действительно, максимальное число без знака получится тогда, когда во всех п двоичных разрядах будут записаны 1, а минимальное число получится тогда, когда во всех разрядах будут записаны 0. Поэтому максимальное значение целого числа без знака, которое можно записать в п двоичных разрядах, можно сосчитать по формуле: 2n-1.
В табл. 2.10 приведены максимальные значения десятичных чисел без знака и соответствующее им число разрядов (бит):
Таблица 2.10
| Число разрядов | Максимальное двоичное число без знака | Максимальное десятичное число без знака |
Таким образом, видно, что при использовании, например, 16-разрядной сетки диапазон представления целых чисел лежит в пределах от 0 до 65535. Заметим, что с увеличением в 2 раза числа разрядов п величина максимального числа, представляемого с их помощью, увеличивается в 2n раз.
Сложение двух чисел без знака в компьютерной арифметике осуществляется аналогично сложению двух двоичных чисел. Так, например, сложение 12+12=102 в обычной двоичной арифметике выглядит так:

а в компьютерной арифметике при восьмиразрядной сетке так:

ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ СО ЗНАКОМ.
Для представления целых чисел со знаком один разряд, как правило, старший, отводится под знак числа. Знак положительного числа кодируется нулем, а знак отрицательного – единицей в этом разряде. Например, двоичное число +100112 (+1910) запишется в 16-разрядном регистре так:

знак числа "+ "
Такая форма представления целых чисел со знаком, когда крайний левый бит разрядной сетки отводится под знак числа, а остальные п-1 бит отводятся под цифры числа в двоичной системе счисления, называется прямым кодом двоичного числа. Причем все разряды должны быть обязательно заполнены, даже если в этих разрядах будет записан "незначащий ноль". Прямой код положительного числа фактически совпадает с самим числом, а прямой код отрицательного числа отличается от положительного только наличием единицы в знаковом разряде. Это означает, что при 16-разрядной сетке прямой код положительного двоичного числа +100112 будет иметь вид 0000000000010011, а прямой код отрицательного двоичного числа -100112 будет отличаться от положительного только содержимым старшего разряда регистра: 1000000000010011.
Естественно, что выделение одного разряда под знак числа приводит к уменьшению имеющихся в нашем распоряжении разрядов регистра на единицу. Поэтому максимальное значение числа, которое можно представить в n -разрядном регистре, также уменьшится. Теперь оно будет равно 2n-1-1 (напомним, что при представлении целых чисел без знака оно равно 2n-1). Например, при использовании 16-разрядной сетки максимальное число, которое можно записать в 16 разрядах, будет равно +3276710, при этом диапазон представления целых положительных чисел также уменьшится и будет находиться в пределах от 0 до +3276710.
Форма представления двоичных чисел в виде прямого кода используется в компьютере только для представления целых положительных чисел. Форма представления отрицательных чисел в виде прямого кода неудобна для реализации арифметических операций в компьютере. Дело в том, что, как это было сказано выше, все арифметические операции в компьютерной арифметике сводятся к двум базовым операциям: сложению и сдвигу. Так, операция вычитания может быть сведена к операции сложения уменьшаемого с вычитаемым, записанным со знаком минус, а операции умножения и деления – к сериям операций сложения и сдвигов.
Сложение положительных чисел в компьютерной арифметике осуществляется над прямыми кодами двоичных чисел. А для реализации операции вычитания используется специальная форма представления отрицательных чисел, называемая дополнительным кодом. Преимущество представления отрицательных чисел в компьютере в виде дополнительного кода состоит прежде всего в том, что такое представление позволяет заменить операцию вычитания простым сложением. При этом операция сложения выполняется над всеми разрядами полученного дополнительного кода, т.е. распространяется и на разряды знаков, рассматриваемых в данном случае как разряды целой части числа.
Дополнительный код отрицательного двоичного числа получается по следующему правилу:
1. Отрицательное двоичное число записывается в прямом коде.
2. Все двоичные разряды, кроме знакового, инвертируются (единицы заменяются нулями, а нули – единицами).
3. К инвертированному числу прибавляется единица по правилам сложения двоичных чисел.
Покажем, как происходит в регистрах компьютера преобразование числа –100112 в дополнительный код при использовании 16-разрядной сетки:
1. число – 100112 в прямом коде записывается в виде:
знак числа “-“
2. разряды с 0 по 14 инвертируются:
знак числа -
3. к младшему разряду инвертированного числа прибавляется 1:
знак числа -
Таким образом, дополнительный код числа -100112 будет иметь вид 1111111111101101.
В табл. 2.11 приведены прямые и дополнительные коды отрицательных десятичных чисел от -1 до -8 (для простоты здесь использована 4-разрядная сетка):
Таблица 2.11
| Десятичное число | Прямой код | Дополнительный код |
| -1 | ||
| -2 | ||
| -3 | ||
| -4 | ||
| -5 | ||
| -6 | ||
| -7 | ||
| -8 | – |
Заметим, что число -8 в дополнительном коде представляется как 1000 (единица в знаковом разряде), а чтобы представить число -8 в прямом коде потребовалось бы разрядов на единицу больше: 11000. Таким образом, для данной длины разрядной сетки (n =4) дополнительным кодом представляется на единицу больше отрицательных чисел, чем положительных: минимальное отрицательное число, которое можно записать в 4-х разрядах в дополнительном коде, равно 1000 (-810), а максимальное положительное равно 0111 (+7). Таким образом, минимальное значение целого числа со знаком, которое можно записать в n -разрядах, равно –2n-1, а максимальное 2n-1–1. Поэтому диапазон представления целых чисел со знаком в n -разрядном регистре находится в пределах от –2n-1 до +(2n-1 –1).
Интересным в табл. 2.11 является также и то, что если начать счет с числа 1000, представляющего дополнительный код числа -810, и двигаться по таблице вверх, то в дополнительном коде каждое следующее число получается прибавлением единицы к предыдущему числу без учета переноса за пределы 4-го разряда. Также происходит и операция вычитания: уменьшаемое складывается с вычитаемым, записанным в дополнительном коде, без учета каких-либо переносов за пределы старшего разряда.
Таким образом, при алгебраическом сложении (алгебраическое сложение - это сложение чисел со знаками) двух двоичных чисел с использованием дополнительного кода положительные слагаемые представляются в компьютере в прямом коде, а отрицательные – в дополнительном. Затем производится суммирование этих кодов, включая разряды знаков. При возникновении переноса из знакового разряда единица переноса отбрасывается, т.к. она вышла за пределы разрядной сетки. В результате получается алгебраическая сумма в прямом коде, если она положительна, и в дополнительном коде, если эта сумма получилась отрицательной.
Приведем примеры выполнения алгебраического сложения:
| В десятичной системе | В компьютерной арифметике |
5  -4 -4  =1 =1 
| 
|
3  -7 -7  =-4 =-4 
| 
|
-2  -6 -6  =-8 =-8 
| 
|
8  -8 -8  =0 =0 
| 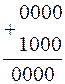
|
В третьем примере получилась единица в "несуществующем" разряде, которая была отброшена, т.к. вышла за пределы выбранной разрядной сетки.
Рассмотрим следующие примеры.
Даны числа: А=3410, В=3010. Вычислим А+В, А-В, В-А, АхВ. Будем считать, что для представления чисел используется 8-разрядная сетка.
1. Найдем сумму А+В:
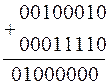
Ноль, полученный в знаковом разряде, свидетельствует о том, что результат - положительное число и он равен 010000002 или 6410.
2. Найдем разность А-В: (число -В в дополнительном коде буде иметь вид 11100010):
+00100010
11100010
Единица, вышедшая за пределы восьмиразрядной сетки, отбрасывается. Ноль в знаковом разряде свидетельствует о том, что результат положительный и равен 1002 или 410.
2. Найдем разность В-А: (число -А в дополнительном коде будет иметь вид 11011110):
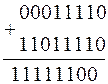
Результат отрицательный и получен в дополнительном коде. Перейдем в прямой код, для этого вычтем 1:
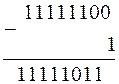
Применим операцию инверсии, не затрагивая знакового разряда, получим прямой код 10000100, а это означает, что результат будет равен -1002 или -410.
Найдем произведение В*А:


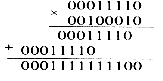
Двоичные разряды произведения, вышедшие за пределы восьмиразрядной сетки, отбрасываются. В результате получим двоичное число 11111100. Единица в знаковом разряде свидетельствует о том, что результат отрицательный и равен -410 против ожидаемого 102010.