Поскольку основным средством хранения, обработки и отображения информации являются компьютеры, то эта информация должна представляться в удобном для этого виде. Как известно, компьютеры могут работать с информацией, представленной в виде последовательностей логических 0 и 1. Следовательно, все виды и формы существующей информации (числовой, текстовой, графической, звуковой и т.д.) должны представляться в виде последовательностей логических 0 и 1. Подобное представление информации, которое используется в компьютерах, называется двоичным кодированием.
ДВОИЧНОЕ КОДИРОВАНИЕ – один из распространенных способов представления информации в силу того, что оно обладает очень важным достоинством: простотой технической реализации элементов с двумя устойчивыми состояниями. Современный компьютер построен именно на таких устройствах и поэтому использует двоичную систему счисления.
Примерами таких простейших устройств являются электронные триггеры, имеющие два устойчивых электрических состояния (относительно высокий или относительно низкий электрический потенциал на выходе), используемые для организации оперативной памяти; магнитные носители, участки поверхности которых могут иметь два устойчивых магнитных состояния с различным уровнем намагниченности (относительно высокий или относительно низкий уровень намагниченности), используемые для организации внешней памяти компьютера; лазерные диски, участки поверхности которых также могут иметь два оптических состояния (отражает или поглощает световой поток).
Интересно отметить, что хотя появление и широкое применение двоичного кодирования для представления информации объясняется в первую очередь простотой его технической реализации, данный тип кодирования, как будет показано ниже, является еще и наиболее экономичным способом кодирования информации.
|
|
Код любого числа можно рассматривать как запись этого числа длиной п в некоторой системе счисления с основанием р:
, (2.7)
где i – номер разряда данного числа, l – количество разрядов,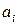 
– множитель, принимающий любые целочисленные значения в пределах от 0 до р-1 и показывающий, сколько единиц i -ого разряда содержится в числе.
При выборе способа кодирования большое значение имеет правильный выбор основания системы счисления р. Заметим, что увеличение основания системы счисления т, с одной стороны, приводит к уменьшению длины кода l, что является позитивным фактором, но, с другой стороны, приводит к необходимости использования вычислительных устройств с большим числом устойчивых состояний.
При кодировании достаточно больших чисел формулу (2.7) можно представить в упрощенном виде, оставив только старший разряд числа:
(2.8)
Если рассматривать возможные значения числа Q как некоторые дискретные его состояния, то энтропия сообщения о данном состоянии будет равна:
. (2.9)
При получении формулы (2.9) полагалось 
, так как величина энтропии не зависит от конкретного значения старшего коэффициента. Величина l, равная:
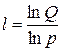(2.10)
представляет собой удельную энтропию сообщения.
При использовании системы счисления с основанием р общая энтропия сообщения будет равна:
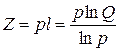. (2.11)
Помимо информационного смысла величина Z характеризует затраты на реализацию представления числа Q в системе счисления с основанием р. Поэтому величина Z может выступать в качестве критерия экономичности того или иного способа кодирования.
|
|
Учитывая вышесказанное, величину р целесообразно находить из условия минимума величины Z. Условие минимума Z записывается в виде:
или, с учетом (2.11) после проведения тождественных преобразований:
. (2.12)
Полагая, что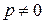 
,получим следующее уравнение, определяющее оптимальное значение т:
,
откуда р=е»2,72.
Таким образом, оптимальным (по соображениям экономности кодирования) основанием системы счисления является дробное число е. Ближайшими к нему целыми числами являются числа 2 и 3. Отсюда в качестве значения оснований целесообразно выбирать р=2 или p =3. Сравнивая системы счисления с этими основаниями с точки зрения удобства физической реализации соответствующих им логических элементов (с двумя устойчивыми состояниями для р=2 и с тремя устойчивыми состояниями для р =3) и простоты выполнения в них арифметических и логических действий, предпочтение необходимо отдать двоичной системе счисления[].
Числовая информация