ТИПОВОЙ РАСЧЕТ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Методические указания и расчетные задания
СОДЕРЖАНИЕ
ВВЕДЕНИЕ……………………………………………………………………..3
1. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЗАКОН РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ..…………4
3. БИНОМИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЗАКОН
РАСПРЕДЕЛЕНИЯ ПУАССОНА……………………………………………..4
3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН………………………………………………………………………6
4. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫИ ЕЕ СВОЙСТВА……………………………………………………………………12
5. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ НЕПРЕРЫВНОЙ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ…………………………………………………14
6. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ
ВЕЛИЧИН……………………………………………………………………..15
7. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ…………………………………….16
8. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ……………………………………...17
9. РАСЧЕТНЫЕ ЗАДАЧИ……………………………………………………19
ИСХОДНЫЕ ДАННЫЕ К РАСЧЕТНЫМ ЗАДАНИЯМ…………………...22
БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………………………..30
ВВЕДЕНИЕ.
Данные методические указания посвящены одному из разделов теории вероятностей “Случайные величины” и являются частью комплекса учебных пособий по курсу высшей математики, направленных на развитие и активизацию самостоятельной работы студентов. В начале каждого параграфа приведены необходимые теоретические сведения и формулы, затем даны решения типовых задач. Задачи составлены так, чтобы они были доступны и по возможности не требовали большой затраты времени на выполнение. Последовательность изложения, терминология и обозначения соответствуют книге автора Гмурмана В. Е. “Введение в теорию вероятностей и математическую статистику”. Методические указания содержат варианты типового расчета по теме “Случайные величины”.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЗАКОН РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.
Случайное событие является качественной характеристикой опыта. Но случайный результат опыта можно охарактеризовать и количественно. Количественной характеристикой случайного опыта является случайная величина.
Случайной величиной называют величину, которая в результате опыта принимает то или иное значение, не известное заранее и зависящее от случайных причин.
ПРИМЕРЫ:1.Число выстрелов до первого попадания в цель.
2.Срок службы бытового прибора.
3.Ошибка измерения.
ОБОЗНАЧЕНИЯ: X, Y, Z …- случайные величины: x, y, z …, - их возможные значения.
Случайную величину называют дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Случайную величину называют непрерывной, если она может принимать все значения из некоторого конечного или бесконечного промежутка числовой прямой. Число возможных значений непрерывной случайной величины всегда бесконечно.
Очевидно, что для задания дискретной случайной величины недостаточно указать все ее возможные значения.
Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей:
| X | x 1 | x 2 | ……. | x n |
| P | p 1 | p 2 | ……. | p n |
Так как в одном испытании случайная величина принимает только одно из возможных значений, то события X = x 1 ,…, X = x n образуют полную группу. Следовательно,
.
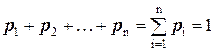БИНОМИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И
ЗАКОН РАСПРЕДЕЛЕНИЯ ПУАССОНА.
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р. Рассмотрим в качестве дискретной случайной величины X – число появлений события А в этих испытаниях. Возможные значения X: 0, 1, 2, …, k, …, n. Вероятности этих возможных значений вычисляются по формуле Бернулли:
P (X = k) = P n(k) = 
,
где k = 0, 1,.2, …, n.
Получили закон распределения:
| X | n | n -1 | … | k | … | |
| P | pn | npn -1 q |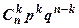 
| … | qn |
Этот закон называют биномиальным.
Если число испытаний n велико, а вероятность появления события р в каждом испытании мала (р £ 0,1), то для нахождения вероятностей пользуются приближенной формулой Пуассона:
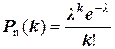, (l = np)
и говорят, что случайная величина распределена по закону Пуассона.
ПРИМЕР 1. Игральная кость брошена три раза. Написать закон
распределения числа появлений шестерки.
РЕШЕНИЕ. X – число появлений «6» в трех испытаниях. Ее возможные значения: 0, 1, 2, 3. Так как вероятность появления «6» при одном бросании кости постоянна и равна 1/6, то случайная величина X распределена по биномиальному закону. Следовательно:
P (X = 0) = q 3 =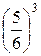 
= 
;
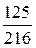P (X = 1) =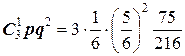 
;
P (X = 2) =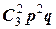 
= 
= 
;
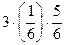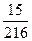P (X = 3) = p 3 =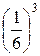 
= 
.
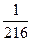| X | ||||
| P |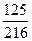 
| 
|
|
|
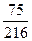
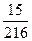
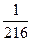
Контроль: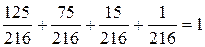 
.
ПРИМЕР 2. Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,01. Найти вероятность того, что в течение одной минуты позвонят: а) ровно три абонента; б) менее трех абонентов; в) более трех абонентов; г) хотя бы один абонент.
РЕШЕНИЕ. Случайная величина X – число позвонивших за 1 мин., распределена по закону Пуассона, то есть
P (X = k)=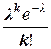 
, где l = np = 100×0,01 = 1.
Таким образом: P (X = k) =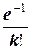 
.
а) Р (X = 3) =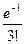 
=0,0613;
б) P (X < 3) = P (X = 0)+ P (X = 1)+ P (X = 2) =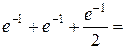 
0,9197;
в) По свойству вероятности противоположных событий
P (X > 3) = 1 – P (X £ 3) = 1 – (P (X < 3) + P (X = 3))=1 – (0,0613+0,9197)=0,019;
г) События “позвонит хотя бы один абонент” и “ни один абонент не позвонит” противоположны, поэтому искомая вероятность:
P (X ³ 1) = 1 – P (X = 0) =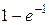 
= 0,632.