ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ

СЛУЧАЙНЫХ ВЕЛИЧИН.

 

Пусть имеется закон распределения случайной величины:

X	x 1	…	x n
P	p 1	…	x n

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:

M (Х) = x ₁ p ₁ + x ₂p₂ + … + x _n p _n =

ЗАМЕЧАНИЯ:

1. Если дискретная случайная величина имеет бесконечно много значений, то существует, если ряд сходится абсолютно.

2. М (Х) – неслучайная, постоянная величина.

Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины и тем точнее, чем больше число опытов. Прежде чем перечислить свойства математического ожидания дадим понятия независимых случайных величин, произведения и суммы случайных величин.

Пусть случайные величины X, Y заданы законами распределения:

X	x 1	...	x n		Y	y 1	…	y n
P	p 1	…	p n	P	g 1	…	g n

Случайные величины X, Y называются, независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Произведением независимых случайных величин Х и Y называют случайную величину XY, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение Y. Вероятность возможных значений х _i у _j равны произведениям вероятностей р _i g _j.

Суммой случайных величин Х и Y называют случайную величину X + Y, возможные значения которой равны суммам каждого возможного значения X с каждым возможным значением Y, вероятности возможных значений X + Y для независимых случайных величин Х и Y равны произведениям вероятностей слагаемых; для зависимых величин – произведениям вероятности одного слагаемого на условную вероятность второго.

 

СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ:

1. М (С) = С, С – постоянная величина;

2. М (СХ) = С × М (Х);

3. Если X, Y – независимые случайные величины, то

М (XY) = М (X)× М (Y);

4. М (X + Y) = М (X) + М (Y);

5. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании:

М (Х) = np.

 

ПРИМЕР 1. Дан перечень возможных значений дискретной случайной величины Х: х ₁ = 1, х ₂ = 2, х ₃ = 3. Найти закон распределения, если М (Х) = 2,3 и М (Х ²) = 5,9.

РЕШЕНИЕ: Если случайная величина Х имеет закон распределения

Х
Р	р 1	р 2	р 3

то величина Х ² задается законом распределения

Х 2
Р	р 1	р 2	р 3

По определению:

М (Х) = р ₁ + 2 р ₂ + 3 р _3,

М (Х ²) = р ₁ + 4 р ₂ + 9 р _3.

Кроме того:

р ₁ + р ₂ + р ₃ = 1.

Получили:

Решая систему, получим: р ₁ = 0,2; р ₂ = 0,3; р ₃ =0,5.

ПРИМЕР 2. Рассмотрим дискретные случайные величины X и Y:

X	-1			Y	-1000
P	0,5	0,5	P	0,5	0,5

Найдем математические ожидания этих величин:

М (Х) = -1 × 0,5 + 1 × 0,5 = 0,

М (Y) = -1000 × 0,5 + 1000 × 0,5 = 0.

Получим: М (Х) = М (Y).

 

ВЫВОД: Одно математическое ожидание полностью случайную величину не характеризует. Полезно знать как рассеяны возможные значения случайной величины вокруг ее математического ожидания.

Отклонением называют разность между случайной величиной и ее математическим ожиданием: Х – М (Х). Если закон распределения случайной величины Х известен:

Х	х 1	…	х n
Р	р 1	…	р n

то отклонение Х – М (Х) имеет следующий закон распределения:

Х – М (Х)	х 1 – М (Х)	…	х n – М (Х)
Р	р 1	…	р n

По свойствам математического ожидания:

М (Х – М (Х)) = М (Х) – М (М (Х)) = М (Х) – М (Х) = 0

Таким образом, среднее значение отклонений не характеризует степень рассеяния случайной величины вокруг ее среднего значения. Поэтому целесообразно рассматривать не отклонения, а их квадраты.

Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонений случайной величины от ее математического ожидания:

D (X) = M [ Х – М (Х)]²

ПРИМЕР 3.Найти дисперсию случайной величины Х, заданной законом распределения:

Х
P	0,3	0,5	0,2

РЕШЕНИЕ.

М (Х) = 1 × 0,3 + 2 × 0,5 + 5 × 0,2 = 2,3

Составим закон распределения квадрата отклонений случайной величины от ее математического ожидания.

[ Х – М (Х)]2	(1 – 2,3) 2 = 1,69	(2 – 2,3) 2 = 0,09	(5 – 2,3) 2 = 7,29
р	0,3	0,5	0,2

D (X) = M [ Х – М (Х)]² = 1,69 × 0,3 + 0,09 × 0,5 + 7,29 × 0,2 = 2,01

Для вычисления дисперсии существует другая, более удобная формула:

D (X) = M (Х ²) – [ М (Х)]²

Составим закон распределения Х ²:

Х
P	0,3	0,5	0,2

Тогда:

M (Х ²) = 1 × 0,3 + 4 × 0,5 + 25 × 0,2 = 7,3; D (X) = 7,3 - 2,3² = 2,01.

 

СВОЙСТВА ДИСПЕРСИИ:

1. D (C) = 0;

2. D (CX) = CD (X);

3. Если X, Y – независимые случайные величины, то

D (X + Y) = D (X) + D (Y);

4. D (C + X) = D (X);

5. D (X – Y) = D (X) + D (Y);

6. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:

D (X) = npq.

Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии:

Среднее квадратическое отклонение также служит для оценки рассеяния возможных значений Х вокруг ее среднего значения. Из определения видно, что D (X) имеет размерность, равную квадрату размерности случайной величины. Значит s (Х) имеет ту же размерность, что и случайная величина Х. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратичное отклонение, а не дисперсию.

Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа ε, определяется неравенством Чебышева:

ПРИМЕР 4. Дискретная случайная величина Х имеет только два возможных значения: х ₁ и х ₂, причем х ₁ < х ₂. Найти закон распределения Х, зная математическое ожидание М (Х) = 2,6 и среднее квадратическое отклонение s (Х) = 0,8. Кроме того известно, что Р (Х = х ₁) = 0,2.

РЕШЕНИЕ. Так как сумма вероятностей всех возможных значений дискретной случайной величины равна единице, то Р (Х = х ₂) = 1 – 0,2 = 0,8.

Напишем закон распределения Х:

Х	х 1	х 2
Р	0,2	0,8

По условию М (Х) = 2,6, следовательно,

0,2 х ₁ + 0,8 х ₂ = 2,6.

Найдем дисперсию:

D (X) = M (Х ²) – [ М (Х)]² = 0,2 х ₁² + 0,8 х ₂² – 2,6².

Тогда:

s (Х) = .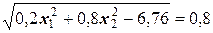

Получаем систему уравнений:

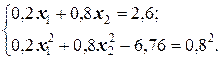
Решая эту систему при условии, что х ₁ < х _2, получим искомый закон распределения:

Х
Р	0,2	0,8

ПРИМЕР 5. Случайные величины X, Y – количество бракованных изделий в партии продукции, поставляемой первым и вторым заводами соответственно, заданы законами распределения:

X					Y
P	0,35	0,05	0,6		G	0,2	0,3	0,5

Найти: а) закон распределения для суммы этих случайных величин;

б) М (X + Y); D (X + Y); в) убедиться, что М (X + Y) = М (X) + М (Y), D (X + Y) = = D (X) + D (Y).

РЕШЕНИЕ.

а) Составим все возможные значения величины Z = X + Y и найдем их вероятности:

z ₁₁ = x ₁+ y ₁ = 1 + 1 = 2, p ₁₁ = p ₁ g ₁ = 0,35 × 0,2 = 0,07;

z ₁₂ = x ₁+ y ₂ = 1 + 2 = 3, p ₁₂ = p ₁ g ₂ = 0,35 × 0,3 = 0,105;

z ₁₃ = x ₁+ y ₃ = 1 + 3 = 4, p ₁₃ = p ₁ g ₃ = 0,35 × 0,5 = 0,175;

z ₂₁ = x ₂+ y ₁ = 2 + 1 = 3, p ₂₁ = p ₂ g ₁ = 0,05 × 0,2 = 0,01;

z ₂₂ = x ₂+ y ₂ = 2 + 2 = 4, p ₂₂ = p ₂ g ₂ = 0,05 × 0,3 = 0,015;

z ₂₃ = x ₂+ y ₃ = 2 + 3 = 5, p ₂₃ = p ₂ g ₃ = 0,05 × 0,5 = 0,025;

z ₃₁ = x ₃+ y ₁ = 3 + 1 = 4, p ₃₁ = p ₃ g ₁ = 0,6 × 0,2 = 0,12;

z ₃₂ = x ₃+ y ₂ = 3 + 2 = 5, p ₃₂ = p ₃ g ₂ = 0,6 × 0,3 = 0,18;

z ₃₃ = x ₃+ y ₃ = 3 + 3 = 6, p ₃₃ = p ₃ g ₃ = 0,6 × 0,5 = 0,3.

Одинаковые значения случайной величины Z объединим, при этом соответствующие вероятности сложим (применяя теорему сложения для несовместных событий). Возможные значения случайной величины запишем в таблице в порядке возрастания и получим закон распределения случайной величины Z = X + Y.

Z = X + Y
Р	0,07	0,115	0,31	0,205	0,3

Контроль: 0,07 + 0,115 + 0,31 + 0,205 + 0,3 = 1.

б) Находим М (X + Y):

М (X + Y) = M (Z) = = 2×0,07 + 3×0,115 + 4×0,31 + 5×0,205 + 6×0,3 = 4,55

Для вычисления дисперсии составим закон распределения Z ² и найдем M (Z ²).

Z 2
Р	0,07	0,115	0,31	0,205	0,3

M (Z ²) = 4 × 0,07 + 9 × 0,115 + 16 × 0,31 + 25 × 0,205 + 36 × 0,3 = 22,2

Находим дисперсию D (X + Y):

D (X + Y) = D (Z) = D (Z ²) - [ M (Z)]² = 22,2 - 4,55² = 1,4975.

в) Убедимся, что М (X + Y) = М (X) + М (Y), D (X + Y) = D (X) + D (Y).

М (X) = 1 × 0,35 +2 × 0,05 + 3 × 0,6 = 2,25;

М (Y) = 1 × 0,2 +2 × 0,3 + 3 × 0,5 = 2,3;

М (X) + М (Y) = 2,25 = 2,3 = 4,55.

Получили: М (X + Y) = М (X) + М (Y).

D (X) = M (Х ²) – [ М (Х)]² = 1 × 0,35 +4 × 0,05 + 9 × 0,6 - 2,25² = 0,8875;

D (Y) = M (Y ²) – [ М (Y)]² = 1 × 0,2 +4 × 0,3 + 9 × 0,5 - 2,3² = 0,61;

D (X) + D (Y) = 0,8875 + 0,61 = 1,4975.

Получили: D (X + Y) = D (X) + D (Y).

ПРИМЕР 6. Вероятность появления события в каждом испытании равна . Пользуясь неравенством Чебышева оценить вероятность того, что число Х появления события будет заключено в пределах от 150 до 250, если будет произведено 800 испытаний.

РЕШЕНИЕ. Случайная величина Х распределена по биномиальному закону. Следовательно:

М (Х) = np =800 × = 200;

D (Х) = npq = 800 × 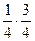= 150.

Найдем максимальную разность между назначенным числом появления события и математическим ожиданием М (Х) = 200:

ε = 250 –200 = 50

Воспользуемся неравенством Чебышева:

Подставив сюда М (Х) = 200, D (Х) = 150, ε = 50, получим:

.