Функция логического умножения (конъюнкция)

Таблицы истинности

Булева функция задаётся конечным набором значений, что позволяет представить её в виде таблицы истинности, например:

x1	x2	…	xn-1	xn	f(x1,x2,…,xn)
		…
		…
		…
		…
{\displaystyle \vdots }	{\displaystyle \vdots }	{\displaystyle \vdots }	{\displaystyle \vdots }	{\displaystyle \vdots }	{\displaystyle \vdots }
		…
		…
		…
		…

 

 

Таблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, у которой значения переменных и значение самой функции выражают истинность. Например, они принимают значения «истина» либо «ложь» (true либо false, 1 либо 0).

 

 

Законны Алгебры Логики.

 

Принцип двойственности

Запишем алгоритм выполнения операций ИЛИ и И, расположив строки таблицы для операции И в обратном порядке – снизу вверх:

Или 0 \/ 0 = 0 0 \/ 1 = 1 1 \/ 0 = 1 1 \/ 1 = 1

И 1 · 1 = 1 1 · 0 = 0 0 · 1 = 0 0 · 0 = 0

Если в этих таблицах переменные заменить их инверсиями, а знаки дизъюнкции на знаки конъюнкции и наоборот, то алгоритмы меняются местами. Таблица истинности для ИЛИ становится таблицей истинности для И и наоборот.

В этом состоит принцип двойственности, который в общем виде записывается так:

, .

Для любого числа переменных это правило, называемое еще теоремой де Моргана, имеет вид:

.

На практике принцип двойственности приводит к тому, что логический элемент, выполняющий в положительной логике операцию И, в случае отрицательной логики будет выполнять операцию ИЛИ.

Для преобразования выражений алгебры логики с целью их упрощения или приведения к удобному виду используются, как и в обычной алгебре, скобки, а если их нет, то сначала выполняется отрицание (инверсия) над отдельными переменными, затем логическое умножение (конъюнкция), затем логическое сложение (дизъюнкция). Если же знак инверсии расположен над целым выражением, то она выполняется в последнюю очередь.

В алгебре логики используется целый ряд теорем.

Теоремы для одной переменной:

A \/ 0 = A 4. A \/ Ā = 1 7. A · A = A

2. A \/ 1 = 1 5. A · 0 = 0 8. A · Ā = 0

3. A \/ A = A 6. A · 1 = 1 9.

Теоремы для двух и более переменных:

10. а) A \/ B = B \/ A, б) AB = BA

переместительный закон, означает, что все входы логического элемента равнозначны.

11. а) A \/ B \/ C = A \/ (B \/ C) = (A \/ B) \/ C,

б) ABC = A(BC) = (AB)C – сочетательный закон.

12. а) A (B \/ C) = AB \/ AC, б) A \/ BC = (A \/ B)(A \/ C) – распределительный закон.

Данная теорема и все последующие вытекают из принципа двойственности. Применим его к выражению 12, а:

– левая часть,

– правая часть.

Введя новые обозначения: , получим обозначения: , а это и есть теорема 12, б.

13. а) A \/ AB = A, б) A(A \/ B) = A

– закон поглощения (A поглощает B).

Доказательство 13, а:

A \/ AB = A(1 \/ B) = A · 1 = A, (используя теоремы 2, 6).

Теорема 13, б следует из принципа двойственности.

14. а) , б) .

Доказательство 14.а:

, (используя теоремы 8 и 1).

Теорема 14, б следует из принципа двойственности.

15. а) AB \/ ĀB = B, į) (A \/ B)(Ā \/ B) = B, закон склеивания (склеивание по A).

Доказательство 15, а:

AB \/ ĀB = B(A \/ Ā) = B · 1 = B, (используя теоремы 4 и 6).

Теорема 15, б следует из принципа двойственности.

 

Основные логические функции.

Функция отрицания

Отрицание – это логическая функция от одной переменной, которая принимает единичное значение при нулевом значении переменной и наоборот. Запись этой функции:

F= .

Конъюнкция может быть обозначена следующими символами:

,¯, не, not.

Черта над переменной x является признаком отрицания (инверсии). Таблица истинности этой функции представлена на рис. 1а. Функция логического отрицания описывает функционирование логического элемента НЕ (рис. 1б).

Условно-графическое обозначение элемента НЕ приведено на рис. 1в. Единичный сигнал на выходе элемента НЕ появляется при нулевом сигнале на входе (x =0,F=1) и, наоборот, нулевой сигнал на выходе появляется при единичном сигнале на входе (x =1,F=0).

 

 

Графически отрицание можно представить с помощью кругов Эйлера (рис. 2).

а) б) в)

x	F

Рис. 1. Элемент НЕ

Рис. 2. Графическое представление отрицания на множестве

Функция логического умножения (конъюнкция)

Логическое умножение – это логическая функция, по крайней мере, от двух переменных, которая принимает единичное значение при единичных значениях всех переменных. Эта функция называется также конъюнкцией. Элементарная конъюнкция зависит от двух переменных. Она принимает единичное значение только тогда, когда и первая переменная и вторая переменная равны единице. Возможны различные варианты записи конъюнкции:

F= ;F= • ;F= ;F= & .

Конъюнкция может быть обозначена следующими символами:

, &, •, ∩, and, и.

Конъюнкция характеризуется таблицей истинности, представленной на рис. 3а. Из рассмотрения таблицы следует, что эта функция принимает единичное значение на наборе 4. Логическое умножение описывает работу элемента И (рис. 3б). Графически конъюнкцию можно представить с помощью кругов Эйлера (рис. 4).

а) б) в)

		F

Рис. 3. Элемент И

Рис. 4. Графическое представление конъюнкции на множествах

Конъюнкция на числовых множествах (операция пересечения): {a,b,c} {b,c,d,e}={b,c}.

Единичный сигнал появляется на выходе этого элемента только при наличии единичного сигнала и на входе 1, и на входе 2.

В общем случае элемент И может иметь n входов (рис. 3в). При этом он реализует конъюнкцию от n переменных, т.е.:

F= • • •…• .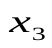