Комплекс условий,Достоверное невозможное и случайное событие.
Достоверное событие — в теории вероятности называется событие 
, которое в результате опыта или наблюдения непременно должно произойти.
Для достоверного события 
Т.е. вероятность события равна единице.
Но, не всякое событие, вероятность которого равна 1, является достоверным
Невозмо́жным собы́тием в теории вероятности называется событие 
, которое в результате опытапроизойти не может.
Очевидно, что вероятность невозможного события равна нулю.
Однако, не всякое событие, вероятность которого равна нулю, является невозможным событием. Пример: событие, состоящее в том, что нормальнораспределенная случайная величина примет некоторое конкретное значение. Для любой непрерывной случайной величины верно утверждение: вероятность того, что случайная величина примет определенное, наперед заданое значение равна нулю. 
Другой пример события с нулевой вероятностью: эксперимент состоит в том, что монета подбрасывается бесконечное число раз. Событие "Монета бесконечное число раз упадет цифрой вверх" имеет нулевую вероятность, но оно может произойти.
Если оговорена некоторая допустимая погрешность (например, 10^(-50)), то событие, вероятность которого не больше значения этой погрешности, называют практически невозможным.
Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.
Пространство элементарных событий
Пространство элементарных событий — множество 
всех взаимно или попарно исключающих друг друга исходов случайного эксперимента, которые вместе образуют полную группу событий.
Элемент этого множества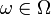 
называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его элементов конечно или счётно. Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (нельзя произносить случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным (континуум). Пространство элементарных событий вместе с алгеброй событий 
ивероятностью 
образует тройку 
, которая называется вероятностным пространством.
3)События.Операции над событиями
Событие-любой набор элементарных исходов или, иными словами, произвольное подмножиство пространства элементарных исходов, называют событием.
Операции над событиями.1)Пересечением(произведением) двух событий А и В называют событие С тогда, когда одновременно происходят оба события А и В. С=АВ 2)События А и В называются несовместными или, непересикающимися если их пересечения являются невозможным событием т.е. АΩВ=ø 3) Обьединением, суммой двух событий А и В называют событие С происходящее только тогда когда происходят хотябы одно из событий А или Вт.е. событие С, состоящее из тех элементарных исходов которые принадлежат хотя бы одному из подмножеств А или В. С=АUВ 4) Разностью 2х событий А и В называют событие С происходящее тогда и только тогда когда происходит событие А но не происходит событие В т.е. событие С состоящее из тех элементарных исходов, которое принадлежит А но не пренадлежит В. С=А\В 5)Дополнением события А(А) Называт событие происходящее тогда когда не происходит событие А. Событие А называют противоположным событию А. А=Ω\А.
4) Алгебра событий
Суммой событий А и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В.
Пример 1. Испытание: стрельба двух стрелков (каждый делает по одному выстрелу). Событие А — попадает в мишень первый стрелок, событие В — попадает в мишень второй стрелок. Суммой событий А и В является событие С = А + В — попадает в мишень по крайней мере один стрелок.
Аналогично, суммой конечного числа событий 
называется событие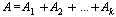 
, состоящее в наступлении хотя бы одного из событий 
.
Из определения суммы событий непосредственно следует, что
А + В = В + А.
Справедливо также и сочетательное свойство. Однако
А + А = А (а не 2 А, как в алгебре).
Произведением событий А и В называется событие С = А В, состоящее в том, что в результате испытания произошли и событие А, и событие В.
Аналогично, произведением конечного числа событий называется событие 
, состоящее в том, что в результате испытания произошли все указанные события.
В Примере 1 произведением событий А и В является событие С = А В, состоящее в попадании в мишень двумя стрелками.
Из определения произведения событий непосредственно следует, что
АВ = ВА.
5) Аксиометрическое опред.вероятностей свойства вероятности.
Вероятностью называется числовая функция, определенная на поле событий S и обладающая следующими свойствами: Аксиома 1. Для любого события A прин. S Р(А)>=0. Аксиома 2. Вероятность достоверного события равна единице Р (омега)=1. Аксиома 3. Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий: А прин. S, В прин. S, А*В=0, Р(А+В)=Р(А)+Р(В). Док-во: Событие А является подмножеством омега, так как А={wi1,…,wim},то, согласно конечной схеме, Р(А)=сумме по l от 1 до m рil, 0<=pil<=1, l=1,…,m, поэтому Р(А)>=0, т.е. условие аксиомы 1 выполняется. Условие аксиомы 2 выполняется, поскольку омега={w1,…,wn}и на основании того, что Р(А)=сумме по l от 1 до m рil, то Р(омега)=сумма по i от 1 до n pi=1. Условие аксиомы 3 также выполняется, так как оно представляет собой содержание теоремы сложения для конечной схемы. Итак, конечная схема является примером объекта, для которого выполняется система аксиом теории вероятностей. Основные свойства вероятности. Пусть задано пространство элементарных событий Е, а вероятности Р определены на событиях из Е. Тогда:
6) Теорема сложения произвольных событий. Вероятность суммы двух произвольных событий равна разности суммы и произведения вероятностей этих событий:
P(A + B) = P(A) + P(B) - P(AB).
Следствие. Вероятность суммы произвольных событий никогда не превосходит суммы вероятностей этих событий:
P(A1 + A2 +...+ An) ≤ P(A1) + P(A2) +...+P(An).
7)Элементы комбинаторики:правило суммы произведения и размещения
Правило суммы. Если некоторый объект 
можно выбрать 
способами, а другой объект 
можно выбрать 
способами, то выбор "либо , либо " можно осуществить 
способами.
Правило произведения. Если объект можно выбрать способами, а после каждого такого выбора другой объект можно выбрать (независимо от выбора объекта 
способами, то пары объектов и можно выбрать 
способами.
Размещениями из элементов по называются такие выборки, которые, имея по элементов, выбранных из числа данных элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.
Число размещений из элементов по обозначим 
Используя основное правило комбинаторики, получаем
Если 
, то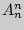 
- число таких размещений, которые отличаются только порядком расположения элементов. Такие размещения называются перестановками. Их число 
находится по формуле
Выборки из элементов, взятых из данных , отличающихся только составом элементов, называются сочетаниями из элементов по . Число 
таких сочетаний находится
9)Класическое опред.вероятности
вероятность есть число, характеризующее степень возможности появления события.
ОПРЕДЕЛЕНИЕ (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Итак, вероятность события А определяется формулой:
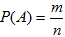(1)
где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.
10) геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.) Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω:
11) Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой
W (А) = m / n,
где m - число появлений события, n - общее число испытаний.
если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах, относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Статистическая вероятность. При статистическом определении в качестве вероятности события принимают его относительную частоту.
где m - число испытаний, в которых событие A наступило, n - общее число произведённых испытаний.
12) Условная вероятность — вероятность одного события при условии, что другое событие уже произошло
Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
| P(AB)=P(A)PA(B) | (4) |
Доказательство. Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2,..., ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из N возможных результатов испытания. Это дает
; 
; 
13) Независимые события.События в совокупн. Попарная независимость
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:
РA (В) = Р (В). (*)
Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми.
Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С.
Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Например, если события A1, A2, А3, независимы в совокупности, то независимы события A1 и А2, А1 и А3, А2 и A3; А1 и A2A3, A2 и A1A3, А3 и A1A2.
14 ) Вероятность появления хотя бы одного из событий А1, А2,..., Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Р (A) = 1 — q 1 q 2... q n.(*)
Доказательство
Ч а с т н ы й с л у ч а й. Если события А1, А2,..., Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий
P (A) = l — q n. (**)
15)Формула полн.вероятности
Формула Бейеса
16) Формула Бернули
в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях)