Пусть в горизонтальном пласте толщины h и ширины B в сечении I-I, совпадающем с контуром питания, поддерживается постоянное давление p к, а в сечении II-II, отстоящем на расстоянии L к от контура питания, поддерживается постоянное давление p г (здесь расположена добывающая галерея) (рисунок. 1.6).
Рисунок. 1.6
Направим ось координат 0 x вдоль линии тока, ось 0 y - вдоль контура питания. Для полного исследования такого потока, как было выяснено ранее, достаточно изучить движение жидкости вдоль оси 0 х.
Дифференциальное уравнение Лапласа при этом примет вид:
(1.1)
Для определения давления в любой точке потока проинтегрируем дважды уравнение (1.1) при следующих граничных условиях:
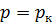при 
;
при 
.
(1.2)
Тогда в результате двукратного интегрирования (1.1) находим последовательно:
или 
,
, (1.3)
где С1 и С2 – произвольные постоянные.
Подставляя в (1.3) граничные условия (1.2), получаем
;
.
(1.4)
Закон распределения давления в пласте найдем, подставив значения постоянных С1 и С2 из (1.4) в (1.3):
.
(1.5)
Из (1.5) получаем выражение для градиента давления
.
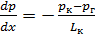(1.6)
Уравнение движения для рассматриваемого случая, как следует из уравнений (1.4), будет иметь вид
.
(1.7)
Тогда, подставив выражение (1.6) для градиента давления, в (1.7) найдем скорость фильтрации
.
(1.8)
Объемный расход жидкости в потоке определяется произведением скорости фильтрации 
на площадь поперечного сечения потока 
, т.е.
.
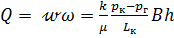(1.9)
Закон движения частиц жидкости 
найдем, используя соотношение между скоростью фильтрации и средней скоростью движения частиц жидкости υ. Имеем
.
Откуда
(1.10)
Подставив выражение (1.8) для скорости фильтрации в (1.10) и интегрируя в пределах от 0 до t и от 0 до x, получим закон движения частиц жидкости
(1.11)
который, используя (1.9), можно представить в виде
.
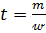
(1.12)
Средневзвешенное по объему порового пространства пластовое давления найдем из выражения
.
(1.13)
В нашем случае
, 
.
(1.14)
Подставив в (1.13) значения 
, 
из (1.14), 
из (1.5) и проинтегрировав, найдем
(1.15)
Рисунок. 1.7 Рисунок. 1.8
Таким образом, характеристики установившегося прямолинейно-параллельного потока несжимаемой жидкости в однородном пласте определяются соотношениями (1.5), (1.6), (1.8), (1.9), (1.11) и (1.15). Анализ этих формул приводит к следующим выводам.
Пластовое давление (1.5) распределяется вдоль линии тока (оси 0 x) по линейному закону Дарси (рисунок 1.7). В любой плоскости y 0 z давление одинаково во всех точках, для которых постоянна абсцисса x, т.е. уравнение
(1.16)
представляет собой уравнение семейства изобар (линий равного давления) – семейства горизонтальных прямых, перпендикулярных к линии тока 0 x.
Поверхностями равного давления в таком потоке будут являться вертикальные плоскости, перпендикулярные к линиям тока 0 x.
Изобары и лини тока (в данном случае и траектории частиц жидкости) образуют два семейства взаимно перпендикулярных линий.
В установившемся прямолинейно-параллельном потоке семейством изобар будут равноотстоящие друг от друга прямые, перпендикулярные к оси 0 x, а семейство траекторий будет представлено прямыми, равноотстоящими друг от друга и параллельными оси 0 x (рисунок. 1.8).
Совокупность изображенных на чертеже изобар и траекторий частиц жидкости называют гидродинамическим полем данного потока. Градиент давления 
(1.6), скорость фильтрации (1.8) и расход (дебит) жидкости Q (1.9) постоянны вдоль потока (не зависят от x) (см рисунок 1.7).
Тот факт, что на рисунке 1.8 изобары и траектории представлены равноотстоящими параллельными прямыми, подтверждает постоянство градиента давления и скорости фильтрации в любой точке потока. Как и следовало ожидать, зависимость между временем t и координатой x (1.11) получилась линейная, ибо в рассматриваемых условиях фильтрационный поток двмжется с постоянной скоростью.
Средневзвешенное пластовое давление p (1.15) равно полусумме значений давлений p ки p г на границах потока, что также находится в полном соответствии с линейным распределением (1.5) давления в пласте.