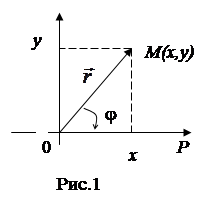
Как известно, положение точки М на плоскости в прямоугольной системе координат определяется парой чисел (х,у) – координатами точки.
 В полярной системе координат та же точка может быть определена так называемым полярным углом j и длиной радиуса – вектора
В полярной системе координат та же точка может быть определена так называемым полярным углом j и длиной радиуса – вектора  (рис.1). Луч ОР называется полярной осью, т.О – полюсом. Связь между декартовым и полярными координатами состоит в следующем:
(рис.1). Луч ОР называется полярной осью, т.О – полюсом. Связь между декартовым и полярными координатами состоит в следующем:  ;
;  .
.
Построить кривые, заданные уравнением в полярной системе координат:
1. r=a j; 2. r= 3(1- cos j); 3. r=asin 3j; 4. r=acos 2j; 5. r 2= a 2 cos 2j.
Вычисление площадей фигур
 а)
а)  площади
площади
криволинейных трапеций, ограниченные кривыми, заданные явными уравнениями в декартовой системе координат (рис.2).
б) Площадь криволинейной трапеции, ограниченной кривой, заданной своими параметрическими уравнениями:
 определяется как
определяется как  .
.
 в) Площадь фигуры, ограниченной кривой, заданной уравнением в полярной системе координат как r=r (j) и лучами j=a, j=b (рис.3), находится
в) Площадь фигуры, ограниченной кривой, заданной уравнением в полярной системе координат как r=r (j) и лучами j=a, j=b (рис.3), находится  .
.
_______________
Найти площади фигур, ограниченных линиями:
1. 4 у =8 х - х 2, 4 у = х +6; 2. у =4- х 2, у = х 2-2 х; 3. ху =4, х =1, х =4, у =0;
4. y=lnx, x=e, y= 0; 5. x=acost, y=bsint; 6. x=a(t-sint), y=a( 1 -cost), осью ОХ, t Î[0;2p]; 7. r=a( 1 -cos j); 8. r 2= a 2 cos 2j. 9. r=asin 3j;
10.  ; r= 2 asin j. 11. r=4 sin 2j; 12. x=acos 3 t; y=asin 3 t.
; r= 2 asin j. 11. r=4 sin 2j; 12. x=acos 3 t; y=asin 3 t.
Ответы:
1.  ; 2. 9; 3. 8 ln 2; 4. 1; 5. p ab; 6. 3p a 2; 7. 3p a 2/2; 8. а 2; 9. p a 2/4;
; 2. 9; 3. 8 ln 2; 4. 1; 5. p ab; 6. 3p a 2; 7. 3p a 2/2; 8. а 2; 9. p a 2/4;
10.  . 11. 6p. 12. 3p/8.
. 11. 6p. 12. 3p/8.
Вычисление длины дуги плоской кривой
1. Дуга задана уравнением y=f(x), x Î[ a,b ]. Длина дуги определяется как  .
.
2. Дуга задана уравнением в параметрической форме  . Тогда
. Тогда  .
.
3. Длина дуги кривой, заданной уравнением в полярной системе координат как r=r (j), jÎ[a,b], определяется:  .
.
____________________
1. Вычислить длину дуги полукубической параболы у 2=(х -1)3 между точками А (2;-1) и В (5;-8).
2. Найти длину дуги кривой у 2= х 3, отсеченной прямой х =4/3.
3. Найти длину одной арки циклоиды x=a(t-sint), y=a( 1 -cost).
4. Найтидлинуастроиды x=acos 3 t, y=asin 3 t.
5. Найти длину кардиоиды r=a( 1+ cos j).
6. Найти длину всей кривой  .
.
Ответы:
1. »7,63; 2. 112/27; 3. 8 а; 4. 6 а; 5. 8 а; 6. 1,5 а p.
Вычисление объема тел вращения
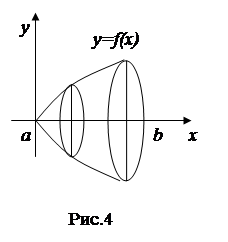
Пусть вокруг оси ОХ вращается криволинейная трапеция, ограниченная непрерывной линией y=f(x) ³0 при условии, что х Î[ a,b ] и осью ОХ (рис.4).Объем полученного тела вращения может быть найден как  .
.
При вращении криволинейной трапеции вокруг оси OY (рис.5) объем 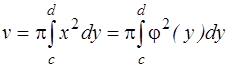 .
.
_____________
1.  Вычислить объем тела, образованного вращением фигуры, ограниченной линиями y 2=2 px, x=a вокруг оси ОХ.
Вычислить объем тела, образованного вращением фигуры, ограниченной линиями y 2=2 px, x=a вокруг оси ОХ.
2. Тело образовано вращением фигуры, ограниченной линиями 2 у=х 2 и 2 х +2 у -3=0 вокруг оси ОХ. Найти объем тела вращения.
3. Вокруг оси ОХ вращается фигура, ограниченная астроидой x=acos 3 t, y=asin 3 t. Найти его объем.
4. Найти объем тела, образованного вращением фигуры, ограниченной линиями  вокруг оси OY.
вокруг оси OY.
Ответы:
1. p ра 2; 2.  ; 3.
; 3. 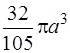 ; 4. 8p.
; 4. 8p.
Несобственные интегралы
Определенный интеграл  предполагает, что пределы интегрирования конечны, а подынтегральная функция f(x) непрерывна на отрезке [ a,b ]. Интегралы, для которых эти условия не выполнены, называются несобственными интегралами.
предполагает, что пределы интегрирования конечны, а подынтегральная функция f(x) непрерывна на отрезке [ a,b ]. Интегралы, для которых эти условия не выполнены, называются несобственными интегралами.
Пусть функция f(x) непрерывна на промежутке [ a;¥). Если существует конечный предел 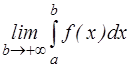 , то его называют несобственным интегралом первого рода, при этом говорят, что несобственный интеграл сходится, если предел не существует или бесконечен, то интеграл расходится.
, то его называют несобственным интегралом первого рода, при этом говорят, что несобственный интеграл сходится, если предел не существует или бесконечен, то интеграл расходится.
В общем случае  , где с – произвольное число.
, где с – произвольное число.
Для ответа на вопрос, сходится или расходится данный интеграл, можно сформулировать следующие признаки:
1. Если на промежутке [ a;¥) непрерывные функции f(x) и j (х) удовлетворяют условию 0£ f(x) £j (x), то из сходимости интеграла 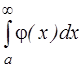 следует сходимость интеграла
следует сходимость интеграла  , а из расходимости интеграла
, а из расходимости интеграла  следует расходимость интеграла
следует расходимость интеграла 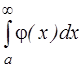 .
.
2. Если существует предел 
j (х) >0, то интегралы  и
и 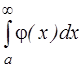 ведут себя одинаково, т.е. оба сходятся или оба расходятся.
ведут себя одинаково, т.е. оба сходятся или оба расходятся.
_________________
Найти несобственные интегралы и сделать вывод об их сходимости:
1.  ; 2.
; 2.  ; 3.
; 3. 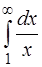 ; 4.
; 4.  ; 5.
; 5.  .
.
Ответы:
1) 1; 2) 1; 3) ¥, расходится; 4) ln 2; 5) p.