Функция с переменными sinx и cosx, над которыми выполняются операции сложения, вычитания, умножения и деления, называется рациональной функцией и обозначается как R(sinx, cosx).
В процессе интегрирования различных тригонометрических выражений часто используются известные тригонометрические формулы:
 . (1)
. (1)
 . (2)
. (2)
 . (3)
. (3)
Можно выделить несколько типов интегралов от тригонометрических функций:
1.  . Он находится с помощью универсальной тригонометрической подстановки:
. Он находится с помощью универсальной тригонометрической подстановки:
 .
.
2. Если подынтегральная функция R(sin x, cos x) нечетна относительно sin x, то можно cos x принять за t; если она нечетна относительно cos x, то за t принимается sin x.
3. Если подынтегральная функция четна относительно sin x и cos x, то за переменную t принимается tgx, т.е. tgx=t; x=arctgt,  ; sin 2 x=
; sin 2 x=  .
.
4.  находятся после понижения степени подынтегральной функции.
находятся после понижения степени подынтегральной функции.
5.  вычисляются после применения к подынтегральным функциям формул (3).
вычисляются после применения к подынтегральным функциям формул (3).
____________________
Найти интегралы:
1.  ; ;
| 2.  ; ;
|
3.  ; ;
| 4.  ; ;
|
5.  ; ;
| 6.  ; ;
|
7. 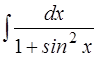 ; ;
| 8.  ; ;
|
9. 
| 10.  ; ;
|
11.  ; ;
| 12. 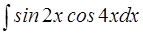 ; ;
|
13.  ; ;
| 14.  ; ;
|
15.  ; ;
| 16.  . .
|
Ответы:
1.  ; 2.
; 2.  ; 3.
; 3.  ;
;
4. 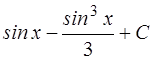 ; 5.
; 5.  ;
;
6.  ; 7.
; 7. 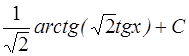 ;
;
8.  ; 9.
; 9.  ;
;
10.  ; 11.
; 11.  ;
;
12.  ; 13.
; 13.  ;
;
14.  или
или
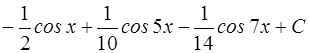 ; 15.
; 15.  ;
;
16.  .
.
Интегрирование иррациональных функций
Некоторые часто встречающиеся интегралы от иррациональных функций можно вычислить методом рационализации подынтегральной функции. Этот метод заключается в отыскании такой подстановки, которая преобразует интеграл от иррациональной функции в интеграл от функции рациональной. Можно выделить следующие типы интегралов от иррациональных функций:
1.  . Для таких интегралов рационализация достигается подстановкой
. Для таких интегралов рационализация достигается подстановкой  , где m – общий знаменатель рациональных чисел Р 1, Р 2,…, Pn.
, где m – общий знаменатель рациональных чисел Р 1, Р 2,…, Pn.
2. Интегралы типа 
 сводятся к табличным после выделения под радикалами полного квадрата и последующей подстановкой
сводятся к табличным после выделения под радикалами полного квадрата и последующей подстановкой  .
.
3. Интегралы типа 
 приводятся к рационально зависящим от тригонометрических функций выражениям с помощью следующих тригонометрических подстановок соответственно: х=asint или x=acost, x=atgt,
приводятся к рационально зависящим от тригонометрических функций выражениям с помощью следующих тригонометрических подстановок соответственно: х=asint или x=acost, x=atgt,  .
.
________________________
Найти интегралы:
1.  ; 2.
; 2.  ; 3.
; 3.  ;
;
4. 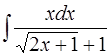 ; 5.
; 5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10.  ;
;
11. 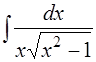 ; 12.
; 12.  .
.
Ответы:
1.  ;
;
2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ;
;
6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ; 11.
; 11. 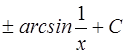 ;
;
12.  .
.
Глава 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определение и вычисление определенного интеграла
Пусть на отрезке [ a,b ] определена функция f(x). Разобьем отрезок [ a,b ] на n частей точками a=x 0< x 1<…< x n =b и на каждом интервале (xi- 1 ,xi) выберем произвольную точку x i. Составим сумму  , где D xi = xi -xi- 1, которая называется интегральной суммой.
, где D xi = xi -xi- 1, которая называется интегральной суммой.
Предел  называется определен-ным интегралом от функции f(x) в пределах от а до b. Вычисляется определенный интеграл по формуле Ньютона-Лейбница, т.е.
называется определен-ным интегралом от функции f(x) в пределах от а до b. Вычисляется определенный интеграл по формуле Ньютона-Лейбница, т.е.  значения первообразной функции для f(x) в точках верхнего и нижнего пределов.
значения первообразной функции для f(x) в точках верхнего и нижнего пределов.
Замена переменной и интегрирование по частям в определенном интеграле
Пусть функция x= j (t) и ее производная x'= j' (t) непрерывны при t Î[a,b], и множеством значений функции x= j (t) при t Î[a,b] является отрезок [ a,b ], и пустьj ( a )=а, j ( b )=b, тогда
 или
или
 .
.
Эта формула называется формулой замены переменной в определенном интеграле.
Интегрирование по частям в определенном интеграле осуществляется по следующей формуле:
 .
.
___________________
Вычислить определенные интегралы:
1. 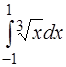 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4. 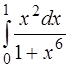 ; 5.
; 5.  ;
;
6.  ; 7.
; 7. 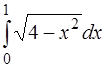 ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  .
.
Ответы:
1. 0; 2.  ; 3. p/6; 4. p/12; 5. p; 6. 7+2 ln 2; 7.
; 3. p/6; 4. p/12; 5. p; 6. 7+2 ln 2; 7. 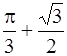 ;
;
8.  ; 9.
; 9.  ; 10.
; 10.  ; 11.
; 11.  ; 12.
; 12.  .
.
Применение определенного интеграла