МАТЕМАТИКА
Интегральное исчисление
Методические указания и задачи
к практическим занятиям для студентов
I курса очной формыобучения
инженерно-технических специальностей
(II семестр)
Брянск 2011
УДК 511
Математика. Интегральное исчисление [Текст]+[Электронный ресурс]: методические указания и задачи к практическим занятиям для студентов I курса очной формыобучения инженерно-технических специальностей (II семестр). – Брянск: БГТУ. - 36с.
Разработали: доц. Ольшевская Н.А.
доц. Цуленева Г.Г.
асс. Алейникова А.О.
Рекомендовано кафедрой «Высшая математика»
(протокол № 2 от 18.10.11).
Научный редактор Гореленков А.И.
Редактор издательства Королева Т.И.
Компьютерный набор Левкина А.П.
Темплан 2011 г., п. 267
Подписано в печать 18.11.11. Формат 60х84 1/16 Бумага офсетная
Офсетная печать. Печ. л. 2,09 Уч.-изд. л. 2.09 Т. 30 экз. Заказ Бесплатно
Издательство Брянского государственного технического университета
Брянск, бульвар 50-летия Октября, 7, тел. 588-249
Лаборатория оперативной печати БГТУ, ул. Институтская, 16
ПРЕДИСЛОВИЕ
Настоящие методические указания ориентированы на студентов I курса очной формы обучения инженерно-технических специальностей и состоят из четырех глав.
В каждой главе приводятся необходимые для практических занятий теоретические сведения и большое количество примеров и задач различного уровня сложности для аудиторной и самостоятельной работы студентов. Все задания снабжены ответами.
Методические указания и подобранные задачи должны помочь студентам освоить данный раздел курса и приобрести устойчивые практические навыки решения задач.
ОГЛАВЛЕНИЕ
Предисловие……………………………………………………..……….3
Глава 1 Неопределенный интеграл………………………………..5
1.1. Понятие неопределенного интеграла……………………. 5
1.2. Основные свойства неопределенного интеграла ………..5
1.3. Таблица основных неопределенных интегралов…………5
1.4. Непосредственное интегрирование и интегрирование
заменой переменной……………………………………….6
1.5. Метод интегрирования по частям………………………..10
1.6. Интегрирование рациональных функций……………….11
1.7. Интегрирование тригонометрических функций………..13
1.8. Интегрирование иррациональных функций……………15
Глава 2. Определенный интеграл………………………………….17
2.1. Определение и вычисление определенного интеграла…17
2.2. Замена переменной и интегрирование по частям в
определенном интеграле………………………………….18
2.3. Применение определенного интеграла………………….19
2.3.1. Полярная система координат……………………19
2.3.2. Вычисление площадей фигур……………………19
2.3.3. Вычисление длины дуги плоской кривой………20
2.3.4. Вычисление объема тел вращения………………21
2.4. Несобственные интегралы………………………………..22
Глава 3. Кратные интегралы………………………………………23
3.1. Двойной интеграл………………………………………...23
3.2. Применение двойного интеграла………………………..26
3.3. Двойной интеграл в полярных координатах……………28
Глава 4. Криволинейные интегралы………………………………29
4.1. Криволинейный интеграл I рода (по длине дуги)………29
4.2. Криволинейный интеграл II рода (по координатам)….31
Список рекомендуемой литературы…………………………………...36
Глава 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Понятие неопределенного интеграла
Функция F(x) называется первообразной функции f(x) на интервале (a,b), если для любого х Î(a,b) выполняется равенство
F'(x)=f(x) или иначе dF(x)=f(x)dx.
Если F(x) является первообразной функции f(x) на (a,b), то множество всех первообразных для f(x) можно задать как F(x)+C, где С – произвольная постоянная. Это множество называется неопределенным интегралом и обозначается как
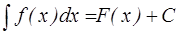 .
.
Основные свойства неопределенного интеграла
1.  ;
;
2.  ;
;
3.  постоянная;
постоянная;
4.  ;
;
5. Если 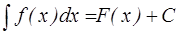 , то и
, то и  , где u= j(u) – произвольная функция, имеющая непрерывную производную.
, где u= j(u) – произвольная функция, имеющая непрерывную производную.
Таблица основных неопределенных интегралов
1. 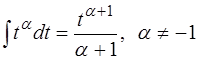 ;
;
1'.  ;
;
1".  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6. 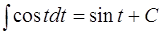 ;
;
7*).  ;
;
8*). 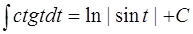 ;
;
9.  ;
;
10.  ;
;
11*).  ;
;
12*).  ;
;
13*).  ;
;
13'.  ;
;
14*).  ;
;
15*).  ;
;
15'. 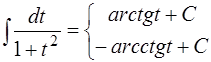 ;
;
16*).  .
.
_____________
*) - интегралы табличными не являются.