Отображение плоскости на себя. Понятие движения
| Цель деятельности учителя
| Создать условия для введения понятий «отображение плоскости на себя», «движение», для построения фигур относительно центра и относительно оси, для рассмотрения свойств осевой и центральной симметрии и их закрепления при решении задач
| | I этап. Актуализация опорных знаний учащихся
| | Цель деятельности
| Совместная деятельность
| | Провести анализ результатов контрольной работы
| 1. Сообщить результаты контрольной работы.
2. Указать ошибки, сделанные учащимися при решении задач.
| | II этап. Повторение темы «Центральная и осевая симметрия»
| | Повторить построение фигур относительно центра симметрии и оси симметрии
| 1. На координатной плоскости имеются точки А (2; 3), В (–4; 6), С (2; 0), D (0; –5). Постройте точки:
а) симметричные А и D относительно оси Оу;
б) симметричные В и С относительно оси Ох;
в) симметричные А и В относительно начала координат.
2. Построить точки, симметричные А и В относительно прямой l.
 Рис. 1
3. Постройте фигуры, симметричные данным относительно прямой l. Рис. 1
3. Постройте фигуры, симметричные данным относительно прямой l.
 Рис. 2
4. Постройте точки, симметричные данным относительно точки О. Рис. 2
4. Постройте точки, симметричные данным относительно точки О.
 Рис. 3
5. Постройте фигуры, симметричные данным относительно точки О. Рис. 3
5. Постройте фигуры, симметричные данным относительно точки О.
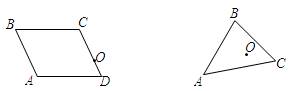 Рис. 4
6. Есть ли точки, для которых не существует точек, симметричных данной относительно: а) прямой; б) точки? Рис. 4
6. Есть ли точки, для которых не существует точек, симметричных данной относительно: а) прямой; б) точки?
| | III этап. Изучение нового материала
| | Ввести понятие отображения плоскости на себя
| 1. Ввести понятие отображения плоскости на себя и проиллюстрировать его примерами осевой и центральной симметрий.
Важно подчеркнуть, что при отображении плоскости на себя выполняются два условия:
1) каждой точке плоскости ставится в соответствие какая-то одна точка плоскости;
2) каждая точка плоскости оказывается поставленной в соответствие какой-то точке плоскости.
Нужно показать, что в случаях осевой и центральной симметрий выполняются оба условия. В качестве контрпримера можно привести соответствие между точками плоскости, при котором каждой точке плоскости ставится в соответствие ее ортогональная проекция на данную прямую. В этом случае нарушено второе условие отображения плоскости на себя: не каждая точка плоскости оказывается сопоставленной какой-то точке, а именно: любая точка, не лежащая на данной прямой, не будет сопоставлена никакой точке плоскости (плоскость отображается не на себя, а на данную прямую).
2. Решить задачи № 1148 (а) и 1149 (а).
3. Ввести понятие движения, опираясь на задачи 3 и 6, рассмотренные в начале урока.
В качестве примера отображения плоскости на себя, не являющегося движением, то есть не сохраняющего расстояния между точками, можно рассмотреть центральное подобие (гомотетию) с коэффициентом 2; учащиеся сами могут доказать, что при таком отображении расстояния между точками увеличиваются в два раза.
4. Решить задачу № 1153 для усвоения понятия, а затем по заранее подготовленному рисунку решить следующую задачу:
При движении плоскости точка А переходит в точку М. В какую из обозначенных на рисунке точек может отобразиться при этом движении точка В?
 Рис. 5 Рис. 5
| | IV этап. Закрепление изученного материала
| | Цель деятельности
| Совместная деятельность
| | Совершенствовать навыки решения задач по изученной теме
| 1. Разобрать решение задачи № 1150.
2. Решить задачи № 1151, 1152 (а, б), 1158.
3. Хотя пункт 119* не является обязательным, учащиеся должны знать, что понятия наложения и движения эквивалентны, а значит при движении любая фигура переходит в равную ей фигуру. Для лучшего усвоения материала этого пункта полезно обсудить решение задачи № 1156 и решить задачи № 1154, 1157, 1155
| | V этап. Итоги урока.
| | Домашнее задание:
| изучить материал пунктов 117–118; ответить на вопросы 1–13, с. 297; решить задачи № 1149 (б), 1148 (б)
| | | | | |
|
Поиск по сайту:
|
 Рис. 1
3. Постройте фигуры, симметричные данным относительно прямой l.
Рис. 1
3. Постройте фигуры, симметричные данным относительно прямой l.
 Рис. 2
4. Постройте точки, симметричные данным относительно точки О.
Рис. 2
4. Постройте точки, симметричные данным относительно точки О.
 Рис. 3
5. Постройте фигуры, симметричные данным относительно точки О.
Рис. 3
5. Постройте фигуры, симметричные данным относительно точки О.
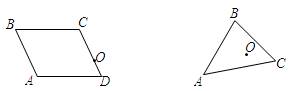 Рис. 4
6. Есть ли точки, для которых не существует точек, симметричных данной относительно: а) прямой; б) точки?
Рис. 4
6. Есть ли точки, для которых не существует точек, симметричных данной относительно: а) прямой; б) точки?
 Рис. 5
Рис. 5