Практическая работа «Равносильные формулы. Составление таблиц истинности»
Теоретическая часть
Равносильные формулы. Основные равносильности
Определение. Формула называется тождественно истинной, или тавтологией, если эта формула принимает значение 1 при всех наборах значений переменных.
Определение. Формула называется тождественно ложной, или противоречием, если эта формула принимает значение 0 при всех наборах значений переменных.
Основные тавтологии
1. 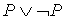
| Закон исключенного третьего |
2. 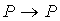
| |
3. 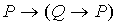
| |
4. 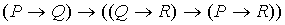
| Цепное рассуждение |
5. 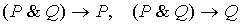
| |
6. 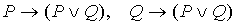
|
Определение. Формулы P и Q называются равносильными (обозначается  ), если при любых значениях переменных значение формулы P совпадает со значением Q.
), если при любых значениях переменных значение формулы P совпадает со значением Q.
Основные равносильности
1. 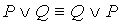 2. 2. 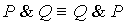
| Коммутативность 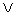 и и 
|
3. 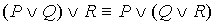 4.
4. 
| Ассоциативность 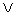 и и 
|
5. 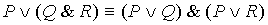 6.
6. 
| Дистрибутивность 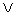 и и 
|
7. 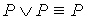 8. 8. 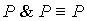
| Идемпотентность 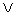 и и 
|
9. 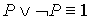 10. 10. 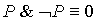
| Законы исключенного третьего и противоречия |
11.  12.
12. 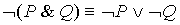
| Законы де Моргана |
13. 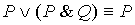 14.
14. 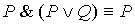
| Законы поглощения |
15. 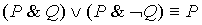
| Правило склеивания |
16. 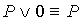 17. 17. 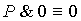 18.
18. 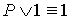 19. 19. 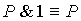
| |
20. 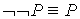
| Закон двойного отрицания |
21. 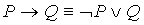 22.
22.  23.
23. 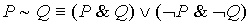 24.
24. 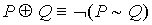
| |
25. 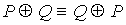
| Коммутативность 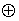
|
26. 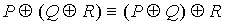
| Ассоциативность 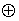
|
27. 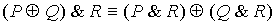
| Дистрибутивность 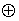 и и 
|
28. 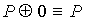 29. 29. 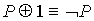 30.
30. 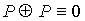
|
Замечание. Здесь P, Q и R —пропозициональные формулы.
Понятие двойственной функции
Определение. Функцией, двойственной к булевой функции  , называется функция
, называется функция 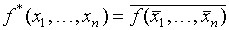 .
.
Определение. Функция называется самодвойственной, если 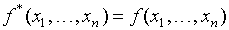 .
.
Теорема. (Принцип двойственности.) Пусть 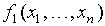 ,…,
,…, 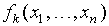 и
и 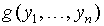 — булевы функции и пусть
— булевы функции и пусть  =
= 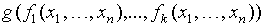 - сложная булева функция. Тогда
- сложная булева функция. Тогда
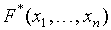 =
= 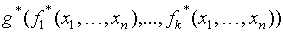
Следствие. Пусть P и Q —формулы. Если  , тогда
, тогда 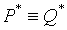 .
.
Принцип двойственности позволяет получать из доказанных равносильностей целый ряд новых. Кроме того, СКНФ(f)= 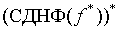 .
.
Некоторые двойственные функции
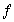
| 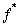
| |
| 1. | 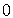
| 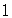
|
| 2. | 
| 
|
| 3. | 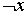
| 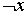
|
| 4. | 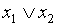
| 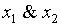
|
| 5. | 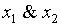
| 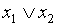
|
Замечание. 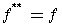 . .
|
Практическая часть
Составим таблицы истинности для логических функций.
Пример.1. Составьте таблицу истинности для формулы 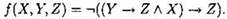
Решение.
| X | Y | Z | Z ^ X | Y → Z ^ X | (Y → Z ^ X) → Z | ((Y → Z ^ X) → Z) |
Пример. 2. Рассмотрим решение этой задачи на примере. Пусть формула F = F(A1, A2, A3) от трёх переменных задана таблицей истинности
Таблица истинности формулы от трёх высказывательных переменных.
| A1 | А2 | А3 | F(A1, A2, A3) |
Понятно, что существует бесконечно много равносильных формул алгебры высказываний, имеющих эту таблицу истинности. Укажем способ нахождения двух таких формул.
Помечаем те строки таблицы, в которых F(A1, A2, A3) принимает значение, равное 1. Это строки 1, 3, 7. Для каждой строки (логической возможности) составим формулу, истинную только в этой логической возможности и ложную во всех остальных логических возможностях
1-я строка — А1 ^ А2 ^ А3
3-я строка — А1 ^ А2 ^ А3
7-я строка — А1 ^ А2 ^ А3.
Если возьмём теперь дизъюнкцию всех этих формул, то это и будет искомой формулой:

Рассмотрим другое решение этой задачи. Помечаем те строки таблицы, в которых F(A1, A2, A3) принимает значение, равное 0. Это строки 2, 4, 5, 6, 8. Для каждой логической возможности составим формулу, ложную только в этой логической возможности и истинную во всех остальных логических возможностях
2-я строка — А1 v А2 v А3
4-я строка — А1 v А2 v А3
5-я строка — А1 v А2 v А3
6-я строка — А1 v А2 v А3
8-я строка — А1 v А2 v А3.
Если теперь возьмём конъюнкцию этих формул, то это также будет искомой, то есть имеющей заданную таблицу истинности, формулой:
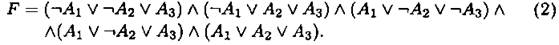
Формулы (1) и (2) равносильны, так как имеют одну и ту же таблицу истинности. В данном случае удобнее строить формулу (1).